[Reinforcement Learning]

在介紹馬爾可夫決策過程之前，我們先介紹下情節性任務和連續性任務以及馬爾可夫性。

情節性任務 vs. 連續任務

• 情節性任務（Episodic Tasks），所有的任務可以被可以分解成一系列情節，可以看作為有限步驟的任務。
• 連續任務（Continuing Tasks），所有的任務不能分解，可以看作為無限步驟任務。

馬爾可夫性

引用維基百科對馬爾可夫性的定義：

馬爾可夫性：當一個随機過程在給定現在狀态及所有過去狀态情況下，其未來狀态的條件機率分布僅依賴于目前狀态。

用數學形式表示如下：

A state \(S_t\) is Markov if and only if

\[P[S_{t+1}|S_t] = P[S_{t+1}|S_1, ..., S_t]

\]

馬爾可夫過程

馬爾可夫過程即為具有馬爾可夫性的過程，即過程的條件機率僅僅與系統的目前狀态相關，而與它的過去曆史或未來狀态都是獨立、不相關的。

馬爾可夫獎賞過程

馬爾可夫獎賞過程（Markov Reward Process，MRP）是帶有獎賞值的馬爾可夫過程，其可以用一個四元組表示 \(<S, P, R, \gamma>\)。

• \(S\) 為有限的狀态集合；
• \(P\) 為狀态轉移矩陣，\(P_{ss^{'}} = P[S_{t+1} = s^{'}|S_t = s]\)；
• \(R\) 是獎賞函數；
• \(\gamma\) 為折扣因子（discount factor），其中 \(\gamma \in [0, 1]\)

獎賞函數

在 \(t\) 時刻的獎賞值 \(G_t\)：

\[G_t = R_{t+1} + \gamma R_{t+2} + ... = \sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}

Why Discount

關于Return的計算為什麼需要 \(\gamma\) 折扣系數。David Silver 給出了下面幾條的解釋：

• 數學表達的友善
• 避免陷入無限循環
• 遠期利益具有一定的不确定性
• 在金融學上，立即的回報相對于延遲的回報能夠獲得更多的利益
• 符合人類更看重眼前利益的特點

價值函數

狀态 \(s\) 的長期價值函數表示為：

\[v(s) = E[G_t | S_t = s]

Bellman Equation for MRPs

\[\begin{align}

v(s)

&= E[G_t|S_t=s]\\

&= E[R_{t+1} + \gamma R_{t+2} + ... | S_t = s]\\

&= E[R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} ... ) | S_t = s]\\

&= E[R_{t+1} + \gamma G_{t+1} | S_t = s]\\

&= E[R_{t+1} + \gamma v(s_{t+1}) | S_t = s]

\end{align}

下圖為MRP的 backup tree 示意圖：


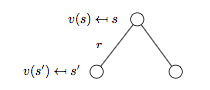
注：backup tree 中的白色圓圈代表狀态，黑色圓點對應動作。

根據上圖可以進一步得到：

\[v(s) = R_s + \gamma \sum_{s' \in S}P_{ss'}v(s')

馬爾可夫決策過程

馬爾可夫決策過程（Markov Decision Process，MDP）是帶有決策的MRP，其可以由一個五元組構成 \(<S, A, P, R, \gamma>\)。

• \(A\) 為有限的動作集合；
• \(P\) 為狀态轉移矩陣，\(P_{ss^{'}}^{a} = P[S_{t+1} = s^{'}|S_t = s,A_t=a]\)；

我們讨論的MDP一般指有限（離散）馬爾可夫決策過程。

政策

政策（Policy）是給定狀态下的動作機率分布，即：

\[\pi(a|s) = P[A_t = a|S_t = a]

狀态價值函數 & 最優狀态價值函數

給定政策 \(\pi\) 下狀态 \(s\) 的狀态價值函數（State-Value Function）\(v_{\pi}(s)\)：

\[v_{\pi}(s) = E_{\pi}[G_t|S_t = s]

狀态 \(s\) 的最優狀态價值函數（The Optimal State-Value Function）\(v_{*}(s)\)：

\[v_{*}(s) = \max_{\pi}v_{\pi}(s)

動作價值函數 & 最優動作價值函數

給定政策 \(\pi\)，狀态 \(s\)，采取動作 \(a\) 的動作價值函數（Action-Value Function）\(q_{\pi}(s, a)\)：

\[q_{\pi}(s, a) = E_{\pi}[G_t|S_t = s, A_t = a]

狀态 \(s\) 下采取動作 \(a\) 的最優動作價值函數（The Optimal Action-Value Function）\(q_{*}(s, a)\)：

\[q_{*}(s, a) = \max_{\pi}q_{\pi}(s, a)

最優政策

如果政策 \(\pi\) 優于政策 \(\pi^{'}\)：

\[\pi \ge \pi^{'} \text{ if } v_{\pi}(s) \ge v_{\pi^{'}}(s), \forall{s}

最優政策 \(v_{*}\) 滿足：

• \(v_{*} \ge \pi, \forall{\pi}\)
• \(v_{\pi_{*}}(s) = v_{*}(s)\)
• \(q_{\pi_{*}}(s, a) = q_{*}(s, a)\)

如何找到最優政策？

可以通過最大化 \(q_{*}(s, a)\) 來找到最優政策：

\[v_{*}(a|s) =

\begin{cases}

& 1 \text{ if } a=\arg\max_{a \in A}q_{*}(s,a)\\

& 0 \text{ otherwise }

\end{cases}

對于MDP而言總存在一個确定的最優政策，而且一旦我們獲得了\(q_{*}(s,a)\)，我們就能立即找到最優政策。

Bellman Expectation Equation for MDPs

我們先看下狀态價值函數 \(v^{\pi}\)。

狀态 \(s\) 對應的 backup tree 如下圖所示：


根據上圖可得：

\[v_{\pi}(s) = \sum_{a \in A}\pi(a|s)q_{\pi}(s, a) \qquad (1)

再來看動作價值函數 \(q_{\pi}(s, a)\)。

狀态 \(s\)，動作 \(a\) 對應的 backup tree 如下圖所示：


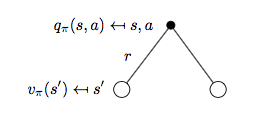
是以可得：

\[q_{\pi}(s,a)=R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{\pi}(s') \qquad (2)

進一步細分 backup tree 再來看 \(v^{\pi}\) 與 \(q_{\pi}(s, a)\) 對應的表示形式。

細分狀态 \(s\) 對應的 backup tree 如下圖所示：


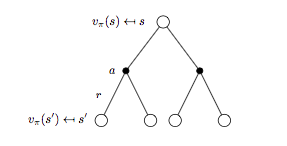
将式子(2)代入式子(1)可以進一步得到 \(v_{\pi}(s)\) 的貝爾曼期望方程：

\[v_{\pi}(s) = \sum_{a \in A} \pi(a | s) \Bigl( R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{\pi}(s') \Bigr) \qquad (3)

細分狀态 \(s\)，動作 \(a\) 對應的 backup tree 如下圖所示：


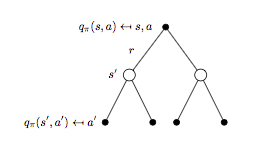
将式子(1)代入式子(2)可以得到 \(q_{\pi}(s,a)\) 的貝爾曼期望方程：

\[q_{\pi}(s,a)=R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a \Bigl(\sum_{a' \in A}\pi(a'|s')q_{\pi}(s', a') \Bigr) \qquad (4)

Bellman Optimality Equation for MDPs

同樣我們先看 \(v_{*}(s)\)：


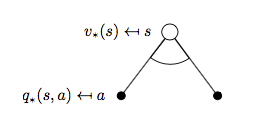
對應可以寫出公式：

\[v_{*}(s) = \max_{a}q_{*}(s, a) \qquad (5)

再來看\(q_{*}(s, a)\)：


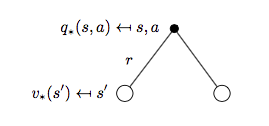
對應公式為：

\[q_{*}(s, a) = R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{*}(s') \qquad (6)

同樣的套路擷取 \(v_{*}(s)\) 對應的 backup tree 以及貝爾曼最優方程：


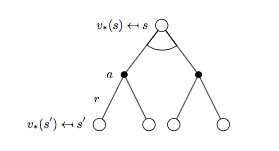
貝爾曼最優方程：

\[v_{*}(s) = \max_{a} \Bigl( R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a v_{*}(s') \Bigr) \qquad (7)

\(q_{*}(s, a)\) 對應的 backup tree 以及貝爾曼最優方程：


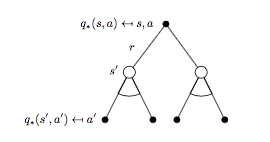
對應的貝爾曼最優方程：

\[R_s^a + \gamma \sum_{s'\in S}P_{ss'}^a\max_{a}q_{*}(s, a) \qquad (8)

貝爾曼最優方程特點

• 非線性（non-linear）
• 通常情況下沒有解析解（no closed form solution）

貝爾曼最優方程解法

• Value Iteration
• Policy Iteration
• Sarsa
• Q-Learning

MDPs的相關擴充問題

• 無限MDPs/連續MDPs
• 部分可觀測的MDPs
• Reward無折扣因子形式的MDPs/平均Reward形式的MDPs

Reference

[1] 維基百科-馬爾可夫性

[2] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018

[3] David Silver's Homepage

作者：Poll的筆記

部落格出處：http://www.cnblogs.com/maybe2030/

本文版權歸作者和部落格園所有，歡迎轉載，轉載請标明出處。

<如果你覺得本文還不錯，對你的學習帶來了些許幫助，請幫忙點選右下角的推薦>