矩陣鍊乘法問題

問題描述：

給定n個矩陣的鍊<A1,A1,A3...An>，矩陣Ai的規模(行列)為pi-1xpi（1<=i<=n），求矩陣鍊的完全括号化方案，使得矩陣乘積A1A2A3...An所需的标量乘法次數最小（假定所給舉證鍊滿足相容性，能夠正确的進行矩陣運算）。

注：假設矩M的規模為pxq，矩陣N的規模為qxr，那麼，矩陣乘法MXN的标量乘法次數為pqr。

分析：

重點在于分析其最優子結構性質，并且導出遞推公式。

有j-i+1個矩陣，進行矩陣鍊乘：AiAi+1Ai+2..AkAk+1...Aj-1Aj，假設其最優括号化方案在Ak這個地方劃分，則整個Ai到Aj矩陣鍊的最低代價三部分相加：

1、前半部分分矩陣鍊AiAi+1Ai+2..Ak（其連乘後的結果是規模為pi-1xpk的矩陣）的最低代價；

2、後半部分矩陣鍊Ak+1...Aj-1Aj（其連乘後的結果是規模為pkxpj的矩陣）最低代價；

3、pi-1xpk階的矩陣與pkxpj階的矩陣相乘的标量乘法次數：pi-1pkpj。

但是是Ak這個分割點是不定的，在Ai到Aj（出Aj外）之間的每矩陣都有可能作為這個最有的劃分點。是以需要找出在周遊意義下的最小代價。

假設C(i,j)是這些矩陣鍊乘的最小代價，那麼遞推式

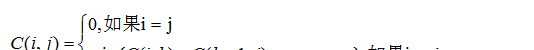
另外，對于輸入資料的處理，因為矩陣鍊都是相容的，是以實際上可以用一個一維數組存儲依次存儲每個矩陣的行列數（要去重）。

例如矩陣鍊A1...A6如下：

可以用一維數組p來存儲：

int[] p = {30,35,15,5,10,20,25};      

A1的規模可以表示為：p[0]xp[1]

A2的規模可以表示為：p[1]x[2]

更一般的，Ai的規模可以表示為p[i-1]xp[i]

算法實作：

package agdp;
public class Matrix {
    public static int getMinCost(int[] p){
        int n = p.length-1;//n為矩陣鍊中矩陣的個數，等于p長度-1
        int[][] aux = new int[n+1][n+1];//輔助數組,為友善計算，第0行和第0列不利用
        for (int l = 2; l <= n; l++) {//矩陣鍊的長度，從2開始，一直到長度為n結束，滿足l=j-i+1
            for (int i = 1,j; i <= n-l+1; i++) {//當j=n是，i到最大值，是以i<=n-l+1
                j = i+l-1;
                aux[i][j] = Integer.MAX_VALUE;
                for (int k = i; k < j; k++) {//周遊Ai到Aj矩陣鍊中每一個位置,并存儲最小者
                    aux[i][j] = Math.min(aux[i][k]+aux[k+1][j]+p[i-1]*p[k]*p[j], aux[i][j]);
                }
            }
        }
        return aux[1][n];
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] p = {30,35,15,5,10,20,25};
        int result = getMinCost(p);
        System.out.println(result);
    }
}      

不同的l=j-i+1鍊的長度會導緻l先鍊從做到右形成一個“滑動視窗”。

其計算過程中全部的子問題的解都存儲在aux數組中，該aux中有效資料是一個上三角矩陣。