算法設計與分析——分治法解棋盤覆寫問題

Description

在一個2k x 2k 個方格組成的棋盤中，恰有一個方格與其他方格不同，稱該方格為一特殊方格，且稱該棋盤為一特殊棋盤。在棋盤覆寫問題中，要用圖示的4種不同形态的L型骨牌覆寫給定的特殊棋盤上除特殊方格以外的所有方格，且任何2個L型骨牌不得重疊覆寫。

Input

k，dr，dc。k定義如前，dr，dc分别表示特殊方格所在的行号和列号 1= < k < =6

Output

按照左上，右上，左下，右下的順序用分治法求解。特殊方格标0，其他位置按上述順序依次标記。

Sample Input

2 1 1

Sample Output

2 2 3 3 
2 0 1 3 
4 1 1 5 
4 4 5 5 


分析：

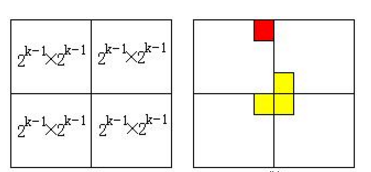
當k>0時，将2k×2k棋盤分割為4個2k-1×2k-1 子棋盤(a)所示。
特殊方格必位于4個較小子棋盤之一中，其餘3個子棋盤中無特殊方格。為了将這3個無特殊方格的子棋盤轉化為特殊棋盤，可以用一個L型骨牌覆寫這3個較小棋盤的會合處，如 (b)所示，進而将原問題轉化為4個較小規模的棋盤覆寫問題。
遞歸地使用這種分割，直至棋盤簡化為棋盤1×1。

這道題其實最應該注意的是棋盤的規模是2k×2k，這個數是4的倍數，這樣也就為原棋盤劃分為四個等大的子棋盤提供了可能，之後的子棋盤也是4的倍數，這樣就能夠一直劃分下去，直到找到那個特殊方格。為了找那個特殊方格，每一個子棋盤都貢獻出了一個方格組成了一個L型骨牌與交彙處，子棋盤接着遞歸的使用這種分隔。

tr，tc的初始值為0,0

dr，dc分别表示特殊方格所在的行号和列号

import java.util.*;
import java.math.*;
public class Main
{
    static int tile = 0;
    public static int[][] board = new int [150][150];

    public void chessBoard(int tr,int tc,int dr,int dc,int size)
    {
        if(size==1)
        {
            return ;
        }
        int t=++tile;//L型骨牌編号
        int s=size/2;//分割棋盤
        //覆寫左上角的棋盤
        if(dr<tr+s&&dc<tc+s)
        {
            //特殊方格在此棋盤中
            chessBoard(tr,tc,dr,dc,s);
        }
        else
        {
            //此棋盤中無特殊方格
            //用t号L型方格覆寫右下角
            board[tr+s-1][tc+s-1]=t;
            chessBoard(tr,tc,tr+s-1,tc+s-1,s);
        }
        //覆寫右上角子棋盤
        if(dr<tr+s&&dc>=tc+s)
        {
            chessBoard(tr,tc+s,dr,dc,s);
        }
        else
        {
            //此棋盤中無特殊方格
            //用t号L型方格覆寫左下角
            board[tr+s-1][tc+s]=t;
            chessBoard(tr,tc+s,tr+s-1,tc+s,s);
        }
        //覆寫左下角子棋盤
        if(dr>=tr+s&&dc<tc+s)
        {
            chessBoard(tr+s,tc,dr,dc,s);
        }
        else
        {
            //此棋盤中無特殊方格
            //用t号L型方格覆寫右上角
            board[tr+s][tc+s-1]=t;
            chessBoard(tr+s,tc,tr+s,tc+s-1,s);
        }
        //覆寫右下角子棋盤
        if(dr>=tr+s&&dc>=tc+s)
        {
            chessBoard(tr+s,tc+s,dr,dc,s);
        }
        else
        {
            //此棋盤中無特殊方格
            //用t号L型方格覆寫左上角
            board[tr+s][tc+s]=t;
            chessBoard(tr+s,tc+s,tr+s,tc+s,s);
        }
    }

    public static void main(String args[])
    {
        Scanner cin = new Scanner(System.in);
        int k,tr,tc,dc,dr;
        k = cin.nextInt();
        dr = cin.nextInt();
        dc = cin.nextInt();
        int size = (int)Math.pow(2,k);
        Main ch = new Main();
        ch.chessBoard(0,0,dr,dc,size);
        for(int i = 0; i < size; i++)
        {
            for(int j = 0; j < size; j++)
            {
                System.out.print(board[i][j] + " ");
            }
            System.out.println();
        }
    }
}

關于參數的說明：

關于時間複雜度：

作者：王陸

出處：https://www.cnblogs.com/wkfvawl/

-------------------------------------------

個性簽名：罔談彼短，靡持己長。做一個謙遜愛學的人！

本站使用「署名 4.0 國際」創作共享協定，轉載請在文章明顯位置注明作者及出處。鑒于部落客處于考研複習期間，有什麼問題請在評論區中提出，部落客盡可能當天回複，加微信好友請注明原因