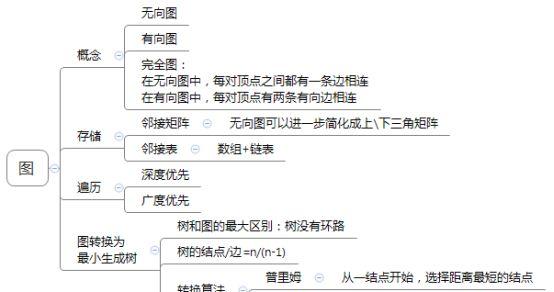
1.
圖是表示物件與物件之間的關系的數學對象,是圖論的基本研究對象,這裡隻是了解點最最基礎的東西。如果圖的每條邊都具有方向性,那麼稱這種圖為有向圖,反之為無向圖。然後,如果在無向圖中,每對頂點之間都有一條邊相連,或者在有向圖中,每對頂點有兩條有向邊相連,則稱為完全圖。
2. 圖的周遊有深度優先和廣度優先兩種方式。
對于上圖的結構,若采用深度優先的方式周遊,則首先通路出發頂點V,然後依次從V出發搜尋V的任意一個鄰接點W,如果W沒有通路過,則從該點出發繼續深度優先周遊。周遊結果可以為:V1, V2, V4, V8, V5, V3, V6, V7。
如果采用廣度優先方式周遊,則先通路出發頂點V,然後通路與頂點V鄰接的全部未通路頂點W, X, Y..., 随後再依次通路 W, X, Y...鄰接的未通路的頂點,是以周遊結果可以為:V1, V2, V3, V4, V5, V6, V7, V8。
3. 圖和樹的的最大差別在于前者是有環路的。将圖轉換為其最小生成樹的過程就是去掉圖中的一部分邊,使之成為權值最小的樹。