動态規劃：爬樓梯

0. 爬樓梯

假設你正在爬樓梯。需要 n 階你才能到達樓頂。

每次你可以爬 1 或 2 個台階。你有多少種不同的方法可以爬到樓頂呢？

注意：給定 n 是一個正整數。

示例 1：

輸入：2

輸出：2

解釋：有兩種方法可以爬到樓頂。

1. 1 階 + 1 階
2. 2 階

示例 2：

輸入：3

輸出：3

解釋：有三種方法可以爬到樓頂。

1. 1 階 + 1 階 + 1 階
2. 1 階 + 2 階
3. 2 階 + 1 階

思路

本題大家如果沒有接觸過的話，會感覺比較難，多舉幾個例子，就可以發現其規律。

爬到第一層樓梯有一種方法，爬到二層樓梯有兩種方法。

那麼第一層樓梯再跨兩步就到第三層 ，第二層樓梯再跨一步就到第三層。

是以到第三層樓梯的狀态可以由第二層樓梯 和 到第一層樓梯狀态推導出來，那麼就可以想到動态規劃了。

我們來分析一下，動規五部曲：

定義一個一維數組來記錄不同樓層的狀态

1. 确定dp數組以及下标的含義

dp[i]：爬到第i層樓梯，有dp[i]種方法

1. 确定遞推公式

如果可以推出dp[i]呢？

從dp[i]的定義可以看出，dp[i] 可以有兩個方向推出來。

首先是dp[i - 1]，上i-1層樓梯，有dp[i - 1]種方法，那麼再一步跳一個台階不就是dp[i]了麼。

還有就是dp[i - 2]，上i-2層樓梯，有dp[i - 2]種方法，那麼再一步跳兩個台階不就是dp[i]了麼。

那麼dp[i]就是 dp[i - 1]與dp[i - 2]之和！

是以dp[i] = dp[i - 1] + dp[i - 2] 。

在推導dp[i]的時候，一定要時刻想着dp[i]的定義，否則容易跑偏。

這展現出确定dp數組以及下标的含義的重要性！

1. dp數組如何初始化

在回顧一下dp[i]的定義：爬到第i層樓梯，有dp[i]中方法。

那麼i為0，dp[i]應該是多少呢，這個可以有很多解釋，但都基本是直接奔着答案去解釋的。

例如強行安慰自己爬到第0層，也有一種方法，什麼都不做也就是一種方法即：dp[0] = 1，相當于直接站在樓頂。

但總有點牽強的成分。

那還這麼了解呢：我就認為跑到第0層，方法就是0啊，一步隻能走一個台階或者兩個台階，然而樓層是0，直接站樓頂上了，就是不用方法，dp[0]就應該是0.

其實這麼争論下去沒有意義，大部分解釋說dp[0]應該為1的理由其實是因為dp[0]=1的話在遞推的過程中i從2開始周遊本題就能過，然後就往結果上靠去解釋dp[0] = 1。

從dp數組定義的角度上來說，dp[0] = 0 也能說得通。

需要注意的是：題目中說了n是一個正整數，題目根本就沒說n有為0的情況。

是以本題其實就不應該讨論dp[0]的初始化！

我相信dp[1] = 1，dp[2] = 2，這個初始化大家應該都沒有争議的。

是以我的原則是：不考慮dp[0]如果初始化，隻初始化dp[1] = 1，dp[2] = 2，然後從i = 3開始遞推，這樣才符合dp[i]的定義。

1. 确定周遊順序

從遞推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，周遊順序一定是從前向後周遊的

1. 舉例推導dp數組

舉例當n為5的時候，dp table（dp數組）應該是這樣的

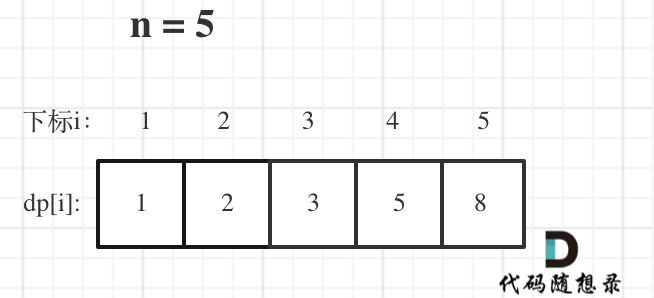
70.爬樓梯

如果代碼出問題了，就把dp table 列印出來，看看究竟是不是和自己推導的一樣。

此時大家應該發現了，這不就是斐波那契數列麼！

唯一的差別是，沒有讨論dp[0]應該是什麼，因為dp[0]在本題沒有意義！

以上五部分析完之後，C++代碼如下：

// 版本一
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n; // 因為下面直接對dp[2]操作了，防止空指針
        vector<int> dp(n + 1);
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) { // 注意i是從3開始的
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};
           

• 時間複雜度：O(n)
• 空間複雜度：O(n)

當然依然也可以，優化一下空間複雜度，代碼如下：

// 版本二
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
};
           

• 空間複雜度：O(1)

後面将講解的很多動規的題目其實都是目前狀态依賴前兩個，或者前三個狀态，都可以做空間上的優化，但我個人認為面試中能寫出版本一就夠了哈，清晰明了，如果面試官要求進一步優化空間的話，我們再去優化。

因為版本一才能展現出動規的思想精髓，遞推的狀态變化。

總結

這道題目和動态規劃：斐波那契數題目基本是一樣的，但是會發現本題相比動态規劃：斐波那契數難多了，為什麼呢？

關鍵是 動态規劃：斐波那契數 題目描述就已經把動規五部曲裡的遞歸公式和如何初始化都給出來了，剩下幾部曲也自然而然的推出來了。

而本題，就需要逐個分析了，大家現在應該初步感受出關于動态規劃，你該了解這些！裡給出的動規五部曲了。