c++智能指針和二叉樹(1): 圖解層序周遊和逐層列印二叉樹

二叉樹是極為常見的資料結構，關于如何周遊其中元素的文章更是數不勝數。

然而大多數文章都是講解的前序/中序/後序周遊，有關逐層列印元素的文章并不多，已有文章的講解也較為晦澀讀起來不得要領。本文将用形象的圖檔加上清晰的代碼幫助你了解層序周遊的實作，同時我們使用現代c++提供的智能指針來簡化樹形資料結構的資源管理。

那麼現在讓我們進入正題。

使用智能指針建構二叉樹

我們這裡所要實作的是一個簡單地模拟了二叉搜尋樹的二叉樹，提供符合二叉搜尋樹的要求的插入功能個中序周遊。同時我們使用shared_ptr來管理資源。

現在我們隻實作

insert

和

ldr

兩個方法，其餘方法的實作并不是本文所關心的内容，不過我們會在後續的文章中逐個介紹：

struct BinaryTreeNode: public std::enable_shared_from_this<BinaryTreeNode> {
    explicit BinaryTreeNode(const int value = 0)
    : value_{value}, left{std::shared_ptr<BinaryTreeNode>{}}, right{std::shared_ptr<BinaryTreeNode>{}}
    {}

    void insert(const int value)
    {
        if (value < value_) {
            if (left) {
                left->insert(value);
            } else {
                left = std::make_shared<BinaryTreeNode>(value);
            }
        }

        if (value > value_) {
            if (right) {
                right->insert(value);
            } else {
                right = std::make_shared<BinaryTreeNode>(value);
            }
        }
    }

    // 中序周遊
    void ldr()
    {
        if (left) {
            left->ldr();
        }

        std::cout << value_ << "\n";

        if (right) {
            right->ldr();
        }
    }

    // 分層列印
    void layer_print();

    int value_;
    // 左右子節點
    std::shared_ptr<BinaryTreeNode> left;
    std::shared_ptr<BinaryTreeNode> right;

private:
    // 層序周遊
    std::vector<std::shared_ptr<BinaryTreeNode>> layer_contents();
};
           

我們的node對象繼承自

enable_shared_from_this

，通常這不是必須的，但是為了在層序周遊時友善操作，我們需要從

this

構造智能指針，是以這步是必須的。

insert

會将比root小的元素插入左子樹，比root大的插入到右子樹；

ldr

則是最為正常的中序周遊，這裡實作它是為了以正常方式檢視tree中的所有元素。

值得注意的是，對于node節點我們最好使用

make_shared

進行建立，而不是将其初始化為全局/局部對象，否則在層序周遊時會因為

shared_ptr

的析構進而導緻對象被銷毀，進而引發未定義行為。

現在假設我們有一組資料：[3, 1, 0, 2, 5, 4, 6, 7]，将第一個元素作為root，将所有資料插入我們的樹中會得到如下的一棵二叉樹：

auto root = std::make_shared<BinaryTreeNode>(3);
root->insert(1);
root->insert(0);
root->insert(2);
root->insert(5);
root->insert(4);
root->insert(6);
root->insert(7);
           

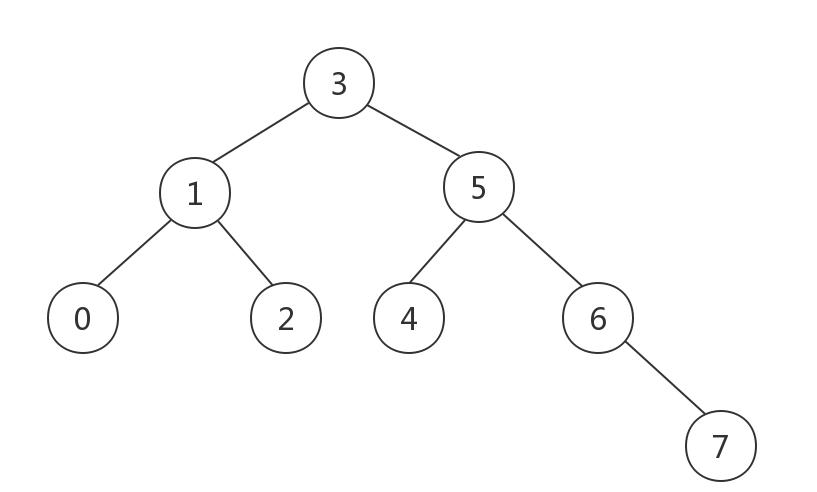
可以看到節點一共分成了四層，現在我們需要逐層列印，該怎麼做呢？

層序周遊

其實思路很簡單，我們采用廣度優先的思路，先将節點的孩子都列印，然後再去列印子節點的孩子。

以上圖為例，我們先列印根節點的值

3

，然後我們再列印它的所有子節點的值，是

1

5

，然後是左右子節點的子節點，以此類推。。。。。。

說起來很簡單，但是代碼寫起來卻會遇到麻煩。我們不能簡單得像中序周遊時那樣使用遞歸來解決問題（事實上可以用改進的遞歸算法），因為它會直接來到葉子節點處，這不是我們想要的結果。不過不要緊，我們可以借助于隊列，把子節點隊列添加到隊列末尾，然後從隊列開頭也就是根節點處周遊，将其子節點添加進隊列，随後再對第二個節點做同樣的操作，遇到一行結束的地方，我們使用

nullptr

做标記。

先看具體的代碼：

std::vector<std::shared_ptr<BinaryTreeNode>>
BinaryTreeNode::layer_contents()
{
    std::vector<std::shared_ptr<BinaryTreeNode>> nodes;
    // 先添加根節點，根節點自己就會占用一行輸出，是以添加了作為行分隔符的nullptr
    // 因為需要儲存this，是以這是我們需要繼承enable_shared_from_this是理由
    // 同樣是因為這裡，當傳回的結果容器析構時this的智能指針也會析構
    // 如果我們使用了局部變量則this的引用計數從1減至0，導緻對象被銷毀，而使用了make_shared建立的對象引用計數是從2到1，沒有問題
    nodes.push_back(shared_from_this());
    nodes.push_back(nullptr); // 為根元素所在層添加分隔符
    // 我們使用index而不是疊代器，是因為添加元素時很可能發生疊代器失效，處理這一問題将會耗費大量精力，而index則無此煩惱
    for (int index = 0; index < nodes.size(); ++index) {
        if (!nodes[index]) {
            // 目前層節點的子節點都已經添加進了隊列此時周遊到了分隔符或已經周遊到隊列末尾
            if (index == nodes.size()-1) {
                break; // 這時我們到達了隊尾，周遊結束
            }

            nodes.push_back(nullptr); // 為目前層的下一層添加分隔符，第一層的節點已經事先添加
            continue;
        }

        if (nodes[index]->left) { // 将目前節點的子節點都添加進隊列
            nodes.push_back(nodes[index]->left);
        }
        if (nodes[index]->right) {
            nodes.push_back(nodes[index]->right);
        }
    }

    return nodes;
}
           

代碼本身并不複雜，重要的是其背後的思想。

算法圖解

如果你第一遍并沒有讀懂這段代碼也不要緊，下面我們有請圖解上線：

首先是循環開始時的狀态，第一行的内容已經确定了(^代表空指針)：

然後我們從首元素開始周遊，第一個周遊到的是root，他有兩個孩子，值分别是1和5：

接着索引值+1，這次周遊到的是nullptr，因為不是在隊列末尾，是以我們簡單添加一個nullptr在隊列末尾，這樣第二行的節點就都在隊列中了：

随後我們開始周遊第二行的節點，将它們的子節點作為第三行的内容放入隊列，最後加上一個行分隔符，以此類推：

簡單來說，就是通過隊列來緩存上一行的所有節點，然後再根據上一行的緩存得到下一行的所有節點，循環往複直到二叉樹的最後一層。當然不隻是二叉樹，其他多叉樹的層序周遊也可以用類似的思想實作。

好了，知道了如何擷取每一行的内容，我們就能逐行處理節點了：

void BinaryTreeNode::layer_print()
{
    auto nodes = layer_contents();
    for (auto iter = nodes.begin(); iter != nodes.end(); ++iter) {
        // 空指針代表一行結束，這裡我們遇到空指針就輸出換行符
        if (*iter) {
            std::cout << (*iter)->value_ << " ";
        } else {
            std::cout << "\n";
        }
    }
}
           

如你所見，這個方法足夠簡單，我們把節點資訊儲存在額外的容器中是為了友善做進一步的處理，如果隻是列印的話大可不必這麼麻煩，不過簡單通常是有代價的。對于我們的實作來說，分隔符的存在簡化了我們對層級之間的區分，然而這樣會導緻浪費至少log2(n)+1個vector的存儲空間，某些情況下可能引起性能問題，而且通過合理得使用計數變量可以避免這些額外的空間浪費。當然具體的實作讀者可以自己挑戰一下，原理和我們上面介紹的是類似的是以就不在贅述了，也可以參考園内其他的部落格文章。

測試

最後讓我們看看完整的測試程式，記住要用make_shared建立root執行個體：

int main()
{
    auto root = std::make_shared<BinaryTreeNode>(3);
    root->insert(1);
    root->insert(0);
    root->insert(2);
    root->insert(5);
    root->insert(4);
    root->insert(6);
    root->insert(7);
    root->ldr();
    std::cout << "\n";
    root->layer_print();
}
           

輸出：

可以看到上半部分是中序周遊的結果，下半部分是層序周遊的輸出，而且是逐行列印的，不過我們沒有做縮進。是以不太美觀。

另外你可能已經發現了，我們沒有寫任何有關資源釋放的代碼，沒錯，這就是智能指針的威力，隻要注意資源的建立，剩下的事都可以放心得交給智能指針處理，我們可以把更多的精力集中在算法和功能的實作上。

另一種層序周遊

上一節提到的方法中我們隻是把節點分層後儲存在容器中等待進一步處理，這樣實作的好處是簡單，然而代價是性能，不僅要存儲額外的分層标志，還需要多次周遊容器。

我們當然可以避免這些弊端，隻要稍微讓代碼複雜一點點：

void layer_print2()
{
    std::queue<NodeType> q;
    q.push(shared_from_this());

    while (!q.empty()) {
        auto layer_len = q.size(); // 擷取目前待處理層中節點的個數

        while (layer_len--) { // 逐個處理目前層内的元素
            auto node = q.front();
            std::cout << node->value_ << " ";

            if (node->left) {
                q.push(node->left);
            }

            if (node->right) {
                q.push(node->right);
            }
            q.pop();
        }

        // 周遊完了一層
        std::cout << std::endl;
    }
}
           

代碼很簡單，不過我還是要解釋一下。

這裡我們借助了隊列，先将每一層的節點都存入隊列，然後我們再獲得隊列的長度，這個長度就是目前待處理層中的節點數。随後我們周遊這些節點，把它們的孩子再存入隊列，形成了下一層待處理的節點。當内層循環結束時就說明目前層已經處理完，這時可以針對該層進行額外的處理，比如我們在這裡輸出一個換行符。

換句話說，在這個方案中我們記錄了每層擁有的節點數以此來确定是否周遊完了一層，而不是額外存儲一個代表目前層次結束的标記符。

智能指針和層序周遊的内容到這裡就結束了，在下一篇文章中我們還将看到智能指針和二叉樹的更多操作。

如有錯誤和疑問歡迎指出！