平面中判斷點在三角形内算法(同向法)

論述了平面判斷點在三角形内外的同向法的兩個注意點。

目錄

• 1. 概述
• 2. 詳論
  • 2.1. 原理與實作
  • 2.2. 注意事項
• 3. 參考

平面中判斷點在三角形内外有很多中算法，文獻1中提到了一種同向法，我認為是比較好的解法，兼顧了效率和可了解性。不過這個算法有兩個要注意的地方。

同向法的具體算法摘錄如下：

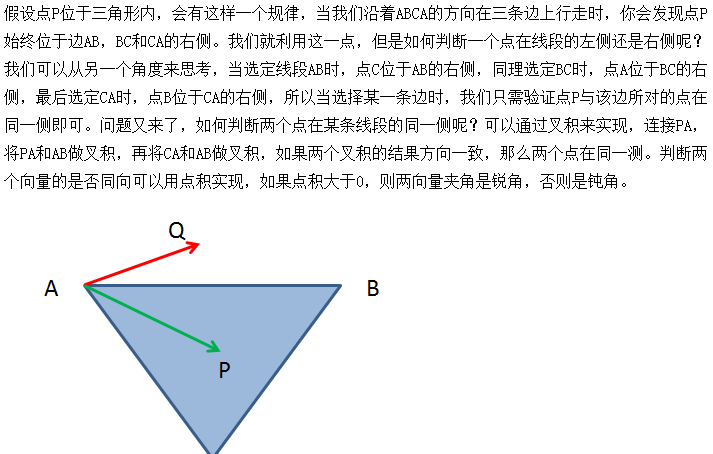
關鍵的實作代碼如下：

//空間三角形
//按照逆時針順序插入值并計算法向量
template <class T>
class Triangle
{
public:
    Vec3<T> v0;
    Vec3<T> v1;
    Vec3<T> v2;

    Triangle()
    {

    }

    Triangle(Vec3<T> v0, Vec3<T> v1, Vec3<T> v2)
    {
        this->v0 = v0;
        this->v1 = v1;
        this->v2 = v2;     
    }

    // v1 = Cross(AB, AC)
    // v2 = Cross(AB, AP)
    // 判斷矢量v1和v2是否同向
    bool SameSide(Vec3<T>& A, Vec3<T>& B, Vec3<T>& C, Vec3<T>& P)
    {
        Vec3<T> AB = B - A ;
        Vec3<T> AC = C - A ;
        Vec3<T> AP = P - A ;

        Vec3<T> v1 = AB ^ AC;
        Vec3<T> v2 = AB ^ AP;

        // v1 and v2 should point to the same direction
        return v1*v2 >= 0 ;
        //return v1 * v2 > 0 ;
    }

    // 判斷平面點P是否在平面三角形内
    bool PointInTriangle2D(Vec3<T>& P)
    {
        Vec3<T> A(v0.x(), v0.y(), 0);
        Vec3<T> B(v1.x(), v1.y(), 0);
        Vec3<T> C(v2.x(), v2.y(), 0);
        return SameSide(A, B, C, P) && SameSide(B, C, A, P) && SameSide(C, A, B, P);
    }
};
           

第一個要注意的是，為了友善表達出向量的叉積，使用了三維向量而不是二維向量。但是這個算法是針對的是平面而不是空間，也就是判斷空間中點是否在三角形内是無效的。并且，傳入的三維向量的第三分量最好都為0，否則，無法保證算法的有效性。

第二是點是通過點積來判斷是否同向：

bool SameSide(Vec3<T>& A, Vec3<T>& B, Vec3<T>& C, Vec3<T>& P)
{
    Vec3<T> AB = B - A ;
    Vec3<T> AC = C - A ;
    Vec3<T> AP = P - A ;

    Vec3<T> v1 = AB ^ AC;
    Vec3<T> v2 = AB ^ AP;

    // v1 and v2 should point to the same direction
    return v1*v2 >= 0 ;
    //return v1 * v2 > 0 ;
}
           

理論上，兩點積等于0，說明兩向量是直角。但是這裡的>=0考慮的是零向量的問題，零向量點乘任何點向量還是0。那麼什麼時候會出現零向量呢？當點正好在三角形的邊界上的時候（兩個相同的向量的叉積為零向量）。也就是說，這裡的=0可以判斷點正好在三角形的邊界或者頂點上，而>0才是判斷點是否在三角形的内部。使用的時候可以靈活掌握。

1. 判斷點是否在三角形内
2. Point in triangle test
3. 二維向量的叉積是标量還是向量？