第十三課:特殊應用:人臉識别和神經風格轉換(Specialapoplications:Face recognition&Neural style transfer)
4.1 什麼是人臉識别?
科普
人臉識别可能一個人的識别準确率是99%,那麼100個人的識别可能需要更高的準确率,99.9%等等。
4.2 One-Shot學習
人臉識别所面臨的一個挑戰就是需要解決一次學習問題,要想讓人臉識别做到一次學習,應該使用Similarity函數,如下圖:
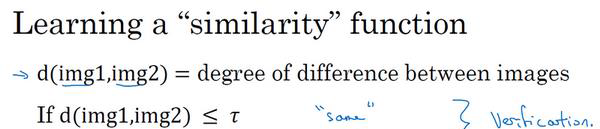
檢視輸入的兩張圖檔(img1,img2)的差異性,如果差異性小于一個數,說明相同,差異性大于一個數,說明不相同。
4.3 Siamese網絡(Siamese network)
Siamese網絡就是首先定義了一個編碼函數,對于輸入的函數,能夠輸出一個128維編碼,如果兩個輸入對應的輸出的範數比較小,就是同一個人,相反,就是不同的人。
4.4 Triplet損失
定義三元組損失函數然後應用梯度下降
上面的公式是損失函數,給出3個圖檔,A、P、N,其中A和P是同一個人,A和N是不同的人,定義損失函數如上,$+\alpha$是為了防止損失函數大于0,損失函數的目的是確定損失函數等于0。
隻要損失函數小于0,則損失函數就是0.
上面的A、P、N就是三元組。
三元組的選擇不能太随意,要選擇很難訓練的A、P、N。下圖是解釋:
4.5 人臉驗證與二分類(Face verification and binary classification)
可以把人臉識别當做二分類問題。
定義輸出$\widehat{y}$如下:
如果相同輸出1,相反輸出0
4.6 神經風格遷移(Neural style transfer)
不得不說,第二張合成圖好陰間。。。
C表示内容圖像,S表示風格圖像,G表示生成的圖像。
4.7 深度卷積網絡學習什麼?(What are deep ConvNets learning?)
網絡第一層能檢測出一些邊緣或顔色陰影等,随着層數的加深,能夠檢測到更複雜的東西。圖中舉例的每個方框代表了不同的9個代表性神經元。
4.8 神經風格遷移系統的代價函數
神經風格遷移系統的代價函數:
$$
J(G)=\alpha {J_{content}}(C,G)+\beta J_{style}(S,G)
第一個是内容代價函數,第二個是風格代價函數。
前面的系數表示權重
上面定義了一個生成圖檔G的代價函數,并将其最小化。
4.9 内容代價函數(Content cost function)
用$a^{[l][C]}$和$a^{[l][G]}$來代表兩個圖檔C和G的l層的激活函數值。如果兩個激活值相似,那麼就意味着兩個圖檔的内容相似,是以:
内容代價函數:
J_{content}(C,G)=\frac{1}{2}||a^{[l][C]}-a^{[l][G]}||^2
通過超參數$\alpha$來調整代價函數。
4.10 風格代價函數(Style cost function)
沒怎麼看懂,給出了一個風格代價函數。
4.11 一維和三維推廣
之前講的卷積都是在2D上讨論的,當然可以以相同的方式來推廣到1D和3D空間。
OVER!