從一些簡單的例子看算法時間複雜度
在程式設計中,一段代碼的執行效率實際上很難估算和預測,其主要受到如下幾個方面的影響:
1.算法依據的數學基礎。
2.編譯器産生的代碼品質和語言的執行效率。
3.問題的輸入規模。
4.硬體的執行速度。
通常情況下,問題的輸入規模和算法的數學基礎是編碼人員需要考慮的條件。時間複雜度是一個用來描述算法執行效率的重要标準。
在了解時間複雜度之前,你應該先了解什麼叫做算法的時間頻度,所謂時間頻度即是一個算法解決問題所消耗的時間。但是一般情況下,一個算法解決問題消耗的時間通常與輸入值有關,例如我們輸入一個整數,找到比它小的所有正偶數,代碼如下:
let n = 10;
for (var i = 0; i < n; i++) {
if (i%2==0) {
console.log(i);
}
} 上面代碼,當輸入n為10時,循環會執行10次,如果時間頻度t,則當輸入n為20時,時間頻度為2t。時間複雜度是用來描述随着問題規模n的變化時間頻度t的變化規律。下面是一段更加數學風格的描述:
一般情況下,算法中基本操作重複執行的次數是問題規模n的某個函數,用T(n)表示,若有某個輔助函數f(n),使得當n趨近于無窮大時,T(n)/f(n)的極限值為不等于零的常數,則稱f(n)是T(n)的同數量級函數。記作T(n)=O(f(n)),稱O(f(n)) 為算法的漸進時間複雜度,簡稱時間複雜度。
計算一個算法的時間複雜度時,我們可以将算法分解為逐條語句,計算每條語句的時間複雜度後再進行累加,如下代碼的作用是對輸入進行求累加:
let n = 10;
let res = 0; //1
for (var i = n; i > 0; i--) { //1+(n+1)+(n+1)
res = i+res; //n
}
console.log(res);//1 當n輸入為10時,時間頻度為1+1+n+1+n+1+n+1 = 3n+5。設算法的時間複雜度函數為f(n),(3n+5)/f(n)當n趨于無窮大時,上式可以簡化為3n/f(n),取f(n)=n,上次結果為非零常數,是以此算法的時間複雜度為f(n)=n,記做O(n)。
當算法的執行時間頻度和n無關時,算法的時間複雜度為O(1),這是時間複雜度最小的函數,但是需要注意,時間複雜度小并不能說明算法執行耗費的時間短,比如一萬行代碼每行隻執行一次的算法時間複雜度也為O(1)。
常見的算法時間複雜度由小到大以此為:
Ο(1)<Ο(log²_n_)<Ο(n)<Ο(nlog²_n_)<Ο(_n_2)<Ο(_n_3)<…<Ο(_2_n)<Ο(n!)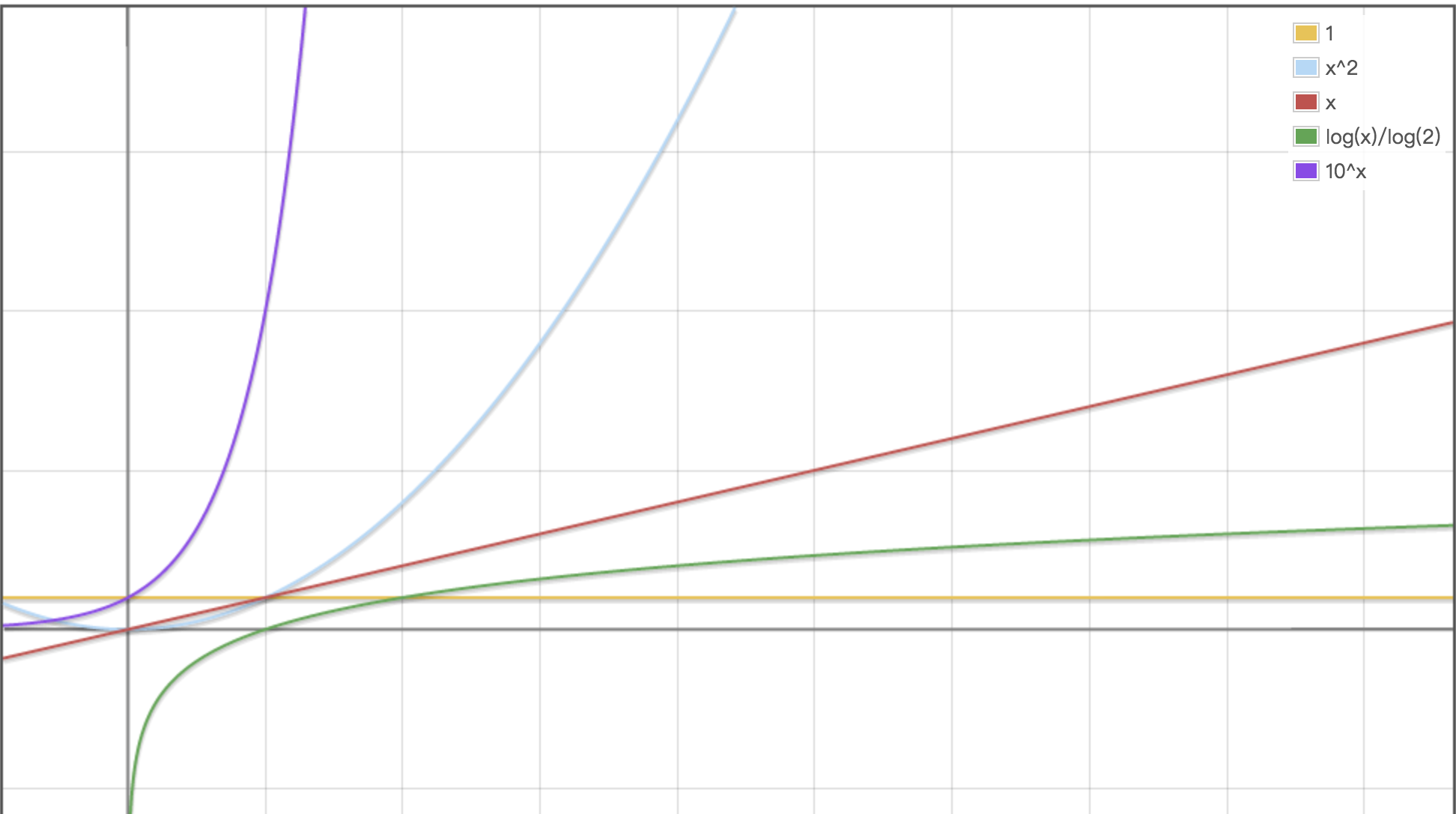
從一些簡單的例子看算法時間複雜度
其中O(log² n)是除了O(1)外時間複雜度最小的函數,例如如下代碼:
let n = 10;
var i = 1;
while(i<n){//2^t<n t<log2(n) t為時間頻度
i = i * 2;
tip++;
} 上面的時間頻度為 1+1+log2(n)+log2(n)+log2(n),去掉常數項後為3log2(n),時間複雜度為O(log2(n))。如果将上面的代碼在加一層循環,則時間複雜度會變為O(nlog3(n)):
let n = 10;
for (var i = 0; i < n; i++) {// 1+n+1+n+1
var j = 1; //n
while(j<n){//[3^t<n t<log3(n)]n t為時間頻度
j = j*3;
}
} 通過上面的示例,也很容易可以看出,循環層數的增多會劇烈的增加算法的時間複雜度,如果在遞歸函數中使用循環,則很容易産生時間複雜度為O(n!)的代碼,從數學上看,這種代碼随着輸入複雜度的增加性能會急劇下降,在使用遞歸加循環時,還是要多多注意,示例代碼如下:
function func(n) { //n
if (n<0) {
return;
}
var i = 0; //n
for (; i < n; i++) { //n*(n-1)*(n-2)...*1
console.log("tip");
}
func(--i);
}
func(10); 上面示例的JavaScript代碼當傳入n為150時的耗時已經和正常循環10000次的相同。