淺談樹鍊剖分

淺談樹鍊剖分

本篇随筆講解圖論中的樹鍊剖分相關内容。

樹鍊剖分是樹上問題的極常用操作，可以說不會樹鍊剖分，一半以上的樹上難題都毫無思路。其重要性不言而喻。想要流暢閱讀本篇部落格并學習樹鍊剖分，需要讀者具有一定的圖論基礎，并對樹形結構和深搜算法有基本的認識。由于本蒟蒻的水準可能不足支援強大的樹剖的講解，是以題解中的一些不足之處敬請大佬們指正。

樹鍊剖分的基本概念

樹鍊剖分，顧名思義，就是把樹拆成鍊。根據樹的形态，我們可以很容易的發現，任何一棵樹都會有很多條鍊正好把樹完全拆分。但是樹鍊剖分并不是單單地把樹拆成鍊。它拆出的鍊有“輕重之分”。

那麼什麼是輕重鍊呢？

這就涉及到了樹鍊剖分的一些基本概念名詞，如下述。

• 重兒子：我們知道，除葉子節點之外，每個節點都會有若幹個兒子節點，而隻要這個節點不是葉子節點，它都是一棵子樹的根。那麼，這個父親節點就有很多個兒子，而一定會有一個兒子的兒子最多，也就是子樹最大。那麼這個兒子節點就叫做\(x\)的重兒子。
• 輕兒子：與重兒子對照了解，重兒子是唯一的，除了重兒子之外的所有兒子都是輕兒子。
• 重邊：父節點與重兒子組成的邊（需要注意的是，這裡的父節點不一定也是重兒子）
• 輕邊：除重邊之外的邊。
• 重鍊：由重邊連起來的鍊叫做重鍊，特别地，一條重鍊的頂部是一個輕兒子。
• 輕鍊：由輕邊連起來的鍊叫做輕鍊。

我們可以通過一張圖來直覺了解：

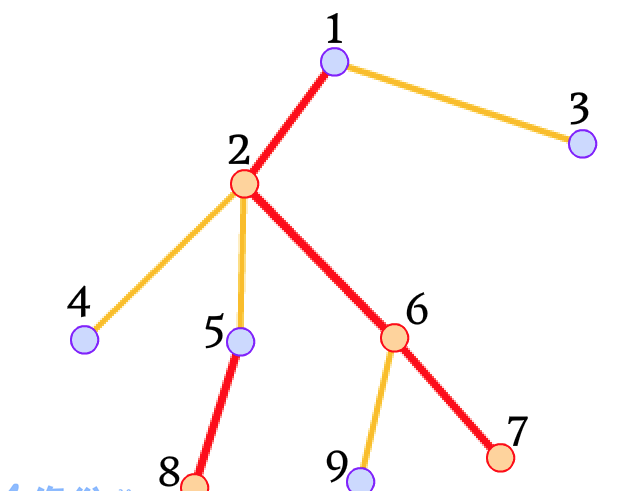
樹鍊剖分解決的問題

樹鍊剖分是樹狀結構的操作，自然解決的是樹上問題。根據我們以上講述的基本概念，我們發現我們可以将一棵樹進行輕重鍊的樹鍊剖分。然後我們就可以把一條鍊上的節點處理成區間的形式（這個了解非常重要！）進而把樹上的問題轉化成了區間問題進行求解。至于區間問題，我們可以采用一些資料結構求解，比如線段樹、樹狀數組等。

一般來講，樹鍊剖分可以解決以下問題：

• 修改兩點路徑上各點的值
• 查詢兩點路徑上各點的值
• 修改某點子樹上各點的值
• 查詢某點子樹上各點的值
• 求解LCA問題

樹鍊剖分的深搜預處理

根據以上的概念了解，我們會發現，若要求解以上問題，我們用樹鍊剖分的好處就是把樹上問題變成區間問題，而區間問題可以用資料結構求解，比如線段樹。但是區間需要編号連續，如果用原樹的節點編号來進行“區間求解”，那顯然是不行的。因為一條鍊上的節點可能是“3.5.7.8.2.1”這樣的亂序，而不是我們想要的一段“連續的數列”，是以這時不能轉換成線段樹求解。為了讓區間連續，我們對整棵樹進行預處理。

樹鍊剖分的核心操作也是預處理。

對于任意節點\(x\)，我們通過DFS處理出它的深度，子樹大小，重兒子編号和父節點編号。這些東西可以用一次深搜處理出來。實質上就是一個樹上周遊的過程。

我們用\(deep[]\)表示深度，\(size[]\)表示子樹大小，\(son[]\)表示重兒子是誰（編号），以及\(fa[]\)表示父節點是誰（編号）。

代碼：

void dfs1(int x,int f)
{
fa[x]=f;
size[x]=1;
deep[x]=deep[f]+1;
for(int i=head[x];i;i=nxt[i])
    {
int y=to[i];
if(y==f)
continue;
dfs1(y,x);
size[x]+=size[y];
if(son[x]==0 || size[y]>size[son[x]])
son[x]=y;
    }
}
      

但是為了進行樹鍊剖分的相關操作，僅僅處理出這些資料是遠遠不夠的。因為有了這些資料，我們隻知道了重鍊的相關資訊，卻依然不能維護出我們需要的那段“連續的區間”。是以，我們需要第二遍深搜。

如何在深搜中保證鍊上節點編号連續呢？

根據深搜的性質和重鍊的性質，我們已經可以隐隐約約的猜到：用DFS序即可。

關于DFS序的相關知識，如有不懂請參照本蒟蒻的這篇部落格：

淺談DFS序

也就是說，我們必然會進行第二遍DFS，而第二遍DFS要處理出的東西就是：每條鍊的頂端節點，每個點的DFS序新編号。

我們用\(top[]\)數組表示每個節點所在鍊的頂端是誰，\(id[]\)數組表示節點的DFS序新編号。

是以有了以下代碼：

void dfs2(int x,int t)
{
id[x]=++cnt;
top[x]=t;
if(!son[x])
return;
dfs2(son[x],t);
for(int i=head[x];i;i=nxt[i])
    {
int y=to[i];
if(y==fa[x] || y==son[x])
continue;
dfs2(y,y);
    }
}
      

這裡有必要說明一下：

我們先處理重兒子後處理輕兒子。

為什麼呢？

因為我們最終的目的是把鍊的新的DFS編号變成連續的。這樣，我們先處理重鍊再處理輕鍊，就能做到：每一條重鍊上的編号是連續的，同時，每一棵子樹上的編号也是連續的。

以上就是樹鍊剖分的核心操作：預處理（預處理竟然變成了核心操作）

樹鍊剖分操作詳解

之後我們回顧一下樹鍊剖分所解決的問題：

通過剛才的預處理，我們已經把樹上節點的新編号變成了連續的。然後我們就可以針對區間（鍊）把原樹變成線段樹來進行我們要做的一系列操作。

先來一份線段樹的基本代碼：

(包括建樹、遞歸修改、遞歸查詢、lazy标記)

void build(int pos,int l,int r)
{
int mid=(l+r)>>1;
if(l==r)
    {
tree[pos]=w[l];
return;
    }
build(lson,l,mid);
build(rson,mid+1,r);
tree[pos]=(tree[lson]+tree[rson]);
}
void mark(int pos,int l,int r,int k)
{
tree[pos]+=(r-l+1)*k;
lazy[pos]+=k;
}
void pushdown(int pos,int l,int r)
{
int mid=(l+r)>>1;
mark(lson,l,mid,lazy[pos]);
mark(rson,mid+1,r,lazy[pos]);
lazy[pos]=0;
}
void update(int pos,int l,int r,int x,int y,int k)
{
int mid=(l+r)>>1;
if(x<=l && r<=y)
    {
mark(pos,l,r,k);
return;
    }
pushdown(pos,l,r);
if(x<=mid)
update(lson,l,mid,x,y,k);
if(y>mid)
update(rson,mid+1,r,x,y,k);
tree[pos]=(tree[lson]+tree[rson]);
}
int query(int pos,int l,int r,int x,int y)
{
int mid=(l+r)>>1;
int ret=0;
if(x<=l && r<=y)
return tree[pos];
pushdown(pos,l,r);
if(x<=mid)
ret+=query(lson,l,mid,x,y);
if(y>mid)
ret+=query(rson,mid+1,r,x,y);
return ret;
}
      

如果讀者已經對線段樹非常熟悉，那麼就會發現：在經過樹鍊剖分的預處理之後，對于上述的4個操作，我們隻需要把節點的新編号（新編号在樹上是按鍊連續的）映射到一個數列上，然後對數列進行線段樹的上述操作即可。

樹鍊剖分求LCA

講這個是為了為下面的鍊上修改做鋪墊。

樹鍊剖分求LCA是比較快速的做法，它的實作原理也比較好了解：

我們每次求LCA（x,y）的時候就可以判斷兩點是否在同一鍊上

如果兩點在同一條鍊上我們隻要找到這兩點中深度較小的點輸出就行了（廢話）

如果兩點不在同一條鍊上：

那就找到深度較大的點令它等于它所在的鍊頂端的父節點即為x=fa[top[x]]：

直到兩點到達同一條鍊上，輸出兩點中深度較小的點即可。

鍊上修改

對于一個修改任意兩點最短路徑上的所有點的操作，我們的一個樸素思路是求出兩點的LCA，然後進行修改。

這就是為什麼講樹鍊剖分求LCA。因為鍊上修改是基于求LCA操作的。

相比于樹鍊剖分求LCA，鍊上修改隻是加了個線段樹的操作而已。

或許代碼能幫你了解一下：

void upd_chain(int x,int y,int k)
{
while(top[x]!=top[y])
    {
if(deep[top[x]]<deep[top[y]])
swap(x,y);
update(1,1,n,id[top[x]],id[x],k);//attention
x=fa[top[x]];
    }
if(deep[x]<deep[y])
swap(x,y);
update(1,1,n,id[y],id[x],k);//attention
}
      

ATTENTION

這裡需要注意的是update時的節點編号問題，以為重新編号是基于DFS序的基礎的，是以根據深搜的性質，每個節點的\(top[]\)肯定要比這個節點的新編号小。

下面的\(id[x],id[y]\)也是這個道理，千萬不要寫反！！

鍊上查詢

鍊上查詢的基本實作思路與鍊上修改大同小異。

直接放代碼：

int q_chain(int x,int y)
{
int ret=0;
while(top[x]!=top[y])
    {
if(deep[top[x]]<deep[top[y]])
swap(x,y);
        (ret+=query(1,1,n,id[top[x]],id[x]))%=mod;
x=fa[top[x]];
    }
if(deep[x]<deep[y])
swap(x,y);
    (ret+=query(1,1,n,id[y],id[x]))%=mod;
return ret;
}
      

樹上修改/查詢

樹上修改/查詢并不需要那麼複雜的操作。我們進行樹上修改/查詢主要運用了樹鍊剖分的一個性質：

以某一個節點為根的子樹編号是這個節點+這個節點的\(size[]\)-1.

即新樹映射到數列上，一棵子樹所占的區間是：\([id[x],id[x]+size[x]-1]\).

這樣就很容易寫樹上修改/查詢的代碼了：

void upd_subtree(int x,int k)
{
update(1,1,n,id[x],id[x]+size[x]-1,k);
}
int q_subtree(int x)
{
return query(1,1,n,id[x],id[x]+size[x]-1);
}
      

在這裡再向大家推薦模闆例題：洛谷3384

題目傳送門

熟練運用樹鍊剖分并解決實際問題是一個提高組/省選選手所必須的一個素質。希望這篇随筆能幫到正在\(OI\)路上奮鬥的你（耶比）。