樹鍊剖分
參考
樹鍊剖分詳解_部落格園_Ivanovcraft
*轉載請注明出處,部分内容引自banananana大神的部落格*
樹刨的定義
樹剖是通過輕重邊剖分将樹分割成多條鍊,然後利用資料結構來維護這些鍊(本質上是一種優化暴力)
定義
父親結點:具有兒子結點的結點(兒子結點:具有父親結點的結點)
重兒子:父親節點的所有兒子中子樹結點數目最多(size最大)的結點;
輕兒子:父親節點中除了重兒子以外的兒子;
- 一個父親結點隻會偏寵愛一個兒子結點(唯一個優先繼承人)。
重邊:父親結點和重兒子連成的邊;
(連續去選擇重兒子連接配接)
輕邊:父親節點和輕兒子連成的邊;
重鍊:由多條重邊連接配接而成的路徑;
輕鍊:由多條輕邊連接配接而成的路徑
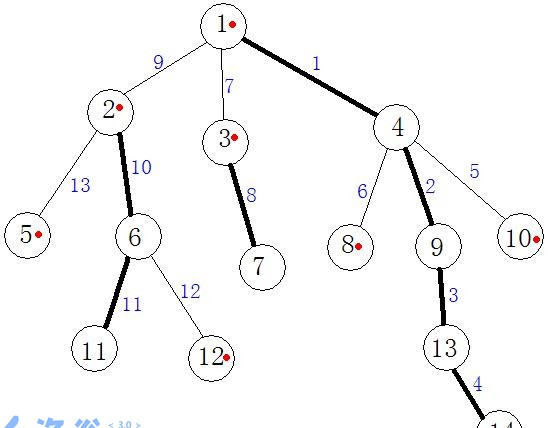
結點1有2,3,4三個兒子結點,其中以2為根節點的子樹總共擁有5個結點,以3為根結點的子樹一共擁有2個結點,以4為根節點的子樹總共擁有6個結點。
因而作為父親結點的1會優先選擇結點4來作為自己的重兒子,而重兒子一旦標明,其他的兒子結點就是其輕兒子。
然後圖中的粗黑線的關系代表的是父親結點和重兒子結點之間的關系,即所謂的
重邊,而其他相對細的邊就為輕邊
而我們可以取多條連續的重邊,用它們來組成重鍊,比如1-4-9-13-14。
而我們可以取多條連續的輕邊,用它們來組成輕鍊,比如1-2-5。
程式實作
由于我們要判斷一個兒子結點是否為重兒子,因為我們就需要把每一個兒子結點所在的子樹的包含的結點的個數給統計出來。
因而,我們需要開辟一個數組,名為size,用來統計子樹的結點個數(其中size[u],代表的以u為根節點的子樹的結點樹),然後也不能白幹活啊,因而我們需要對重兒子進行保留,開辟一個數組名為son(其中son[u]代表的是結點u的重兒子)。
- 關于重兒子的讨論
如果一個點的多個兒子所在子樹大小相等且最大
那随便找一個當做它的重兒子就好了
葉節點沒有重兒子,非葉節點有且隻有一個重兒子
然後再進行标記(跑dfs)的時候為了不回到父親結點,我們可以再定義一個數組
f
(其中f[x]表示的是x結點的父親結點)
然後這裡已經做完了預處理操作了。
void dfs1(int u,int fa,int depth)
{
f[u]=fa;//root結點的父親結點可以令為-1或0
d[u]=depth;//随着遞歸的深度而改變
size[u]=1;//初始化本子樹的結點數,然後再搜尋的過程中給彙集起來
for(周遊u的邊)
{
提取邊上的另一個端點v
若是v是父親結點就跳過
否則往深繼續跑dfs;
size[u]+=size[v];//自下而上返還得到結點數
if(size[v]>size[son[u]])//篩選出真正的重兒子
son[u]=v;
}
}
dfs1(root,0或者-1,1);
dfs跑完大概是這樣的,大家可以手動模拟一下
(逃命)
做個小的總結
| 數組名稱 | 解釋 |
|---|---|
| f | 表示目前結點的父親結點,若其值為0或者-1,代表該點是root。 |
| d | 表示目前結點的深度,是父親結點的深度加一,為了保證數組不越界,可使根節點的父親結點為0。 |
| size | 表示以目前結點為根節點的子樹的總結點樹。 |
| son | 表示目前結點的重兒子,如果其值為0,表示目前結點為葉子結點,不具備有任何的兒子結點。 |
第一遍的dfs提前處理好每一個可行的結點的重兒子結點是哪一個,但仍還沒有形成鍊,因而我們還需要對圖再進行一次統計操作(再跑一遍dfs)
然後關于重鍊的探索,我們很清楚得知道得是目前結點連上它的重兒子結點可以形成一條重邊,而這條重邊就是重鍊的一個組成部分。而對于它的輕兒子來說,也不要灰心,它可能本身就是一條重鍊的頂端結點(為什麼說是可能呢?因為這個結點可能是一個葉子結點,它是無法再繼續形成一條重鍊的,也就是圖中的結點5。
關于第二遍dfs我們需要準備的數組有top,(其中
top[x]
代表結點x的所在鍊的鍊頭結點),也就是說如果有
top[x]==top[y]
,則說明結點x和結點y是在同一條重鍊上。
-
son[x]==0
void dfs2(int u,int t)//目前結點,目前結點所處在的重鍊的頂端
{
top[u]=t;
//id[u]=++cnt;//dfs序,對點的重新标号,這步是為了後面線段樹的操作
//rk[cnt]=u;//從新标号重新映射回去到實際結點
if(!son[u])
reutrn ;
dfs2(son[u],t);//再續良緣
for(掃描u的邊)
{
提取邊上的另一個端點v
如果v不是u的重兒子且不是u的父親結點的話
dfs2(v,v); //以輕兒子為新的一條可能的重鍊的頂端和新的目前結點dfs下去
}
}
| top | 目前結點所在的重鍊的鍊頭結點 |
| id | 目前在dfs2實際通路得到的順序,由于dfs2的設計,是以一條重鍊的id是連續的(這點這是線段樹的可以用來維護重鍊的一個很重要的前提條件) |
| rk | 通過dfs2序重新映射回起初的結點編号 |
int sum(int x,int y)//代表的是x和y兩個結點
{
int ans=0,fx=top[x],fy=top[u];
while(fx!=fy)//如果x和y不在同一條重鍊
{
if(d[fx]>=d[fy])//x的重鍊鍊頭結點比y的重鍊鍊頭結點的深度還低。
{
ans+=query(u,id[fx],id[x]);
x=f[fx],fx=top[x];//将x設定其重鍊鍊頭結點的父親結點,fy為新結點所在重鍊的鍊頭結點。
}
else
{
ans+=query(u,id[fy],id[y]);
y=f[fy],fy=top[y];
}
}
//while語句處理完後,x,y兩個結點将同時處于一條重鍊上,也就意味這我們要單獨去處理這兩點之間的貢獻
if(id[x]<=id[y])//由于線段樹區間的特性,要找到id比較小的,讓它排到前面去
ans+=query(u,id[x],id[y]);
else
ans+=query(u,id[y],id[x]);
return ans;
}