之前有提到在put操作時,如果發現連結清單結構中的元素超過了TREEIFY_THRESHOLD(預設為8),則會把連結清單轉換為紅黑樹,已便于提高查詢效率。代碼如下:
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i); 下面部落客将詳細分析整個過程,并用一個連結清單轉換為紅黑樹的過程為案例來分析。博文從如下幾個方法進行分析闡述:
- 紅黑樹
- ConcurrentHashMap連結清單轉紅黑樹源碼分析
- 連結清單轉紅黑樹案例
先看紅黑樹的基本概念:紅黑樹是一課特殊的平衡二叉樹,主要用它存儲有序的資料,提供高效的資料檢索,時間複雜度為O(lgn)。紅黑樹每個節點都有一個辨別位表示顔色,紅色或黑色,具備五種特性:
- 每個節點非紅即黑
- 根節點為黑色
- 每個葉子節點為黑色。葉子節點為NIL節點,即空節點
- 如果一個節點為紅色,那麼它的子節點一定是黑色
- 從一個節點到該節點的子孫節點的所有路徑包含相同個數的黑色節點
請牢記這五個特性,它在維護紅黑樹時選的格外重要
紅黑樹結構圖如下:
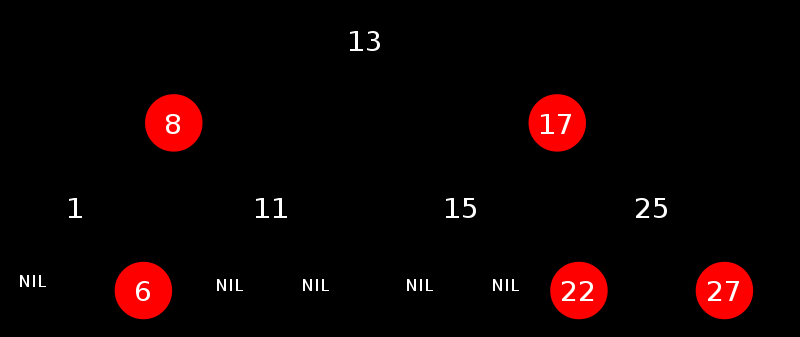
對于紅黑樹而言,它主要包括三個步驟:左旋、右旋、着色。所有不符合上面五個特性的“紅黑樹”都可以通過這三個步驟調整為正規的紅黑樹。
旋轉
當對紅黑樹進行插入和删除操作時可能會破壞紅黑樹的特性。為了繼續保持紅黑樹的性質,則需要通過對紅黑樹進行旋轉和重新着色處理,其中旋轉包括左旋、右旋。
左旋
左旋示意圖如下:
左旋處理過程比較簡單,将E的右孩子S調整為E的父節點、S節點的左孩子作為調整後E節點的右孩子。
右旋
紅黑樹插入節點
由于連結清單轉換為紅黑樹隻有添加操作,加上篇幅有限是以這裡就隻介紹紅黑樹的插入操作,關于紅黑樹的詳細情況,煩請各位Google。
在分析過程中,我們已下面一顆簡單的樹為案例,根節點G、有兩個子節點P、U,我們新增的節點為N
紅黑樹預設插入的節點為紅色,因為如果為黑色,則一定會破壞紅黑樹的規則5(從一個節點到該節點的子孫節點的所有路徑包含相同個數的黑色節點)。盡管預設的節點為紅色,插入之後也會導緻紅黑樹失衡。紅黑樹插入操作導緻其失衡的主要原因在于插入的目前節點與其父節點的顔色沖突導緻(紅紅,違背規則4:如果一個節點為紅色,那麼它的子節點一定是黑色)。
要解決這類沖突就靠上面三個操作:左旋、右旋、重新着色。由于是紅紅沖突,那麼其祖父節點一定存在且為黑色,但是叔父節點U顔色不确定,根據叔父節點的顔色則可以做相應的調整。
1 叔父U節點是紅色
如果叔父節點為紅色,那麼處理過程則變得比較簡單了:更換G與P、U節點的顔色,下圖(一)。
當然這樣變色可能會導緻另外一個問題了,就是父節點G與其父節點GG顔色沖突(上圖二),那麼這裡需要将G節點當做新增節點進行遞歸處理。
2 叔父U節點為黑叔
如果目前節點的叔父節點U為黑色,則需要根據目前節點N與其父節點P的位置決定,分為四種情況:
- N是P的右子節點、P是G的右子節點
- N是P的左子節點,P是G的左子節點
- N是P的左子節點,P是G的右子節點
- N是P的右子節點,P是G的左子節點
情況1、2稱之為外側插入、情況3、4是内側插入,之是以這樣區分是因為他們的處理方式是相對的。
2.1 外側插入
以N是P的右子節點、P是G的右子節點為例,這種情況的處理方式為:以P為支點進行左旋,然後交換P和G的顔色(P設定為黑色,G設定為紅色),如下:
左外側的情況(N是P的左子節點,P是G的左子節點)和上面的處理方式一樣,先右旋,然後重新着色。
2.2 内側插入
以N是P的左子節點,P是G的右子節點情況為例。内側插入的情況稍微複雜些,經過一次旋轉、着色是無法調整為紅黑樹的,處理方法如下:先進行一次右旋,再進行一次左旋,然後重新着色,即可完成調整。注意這裡兩次右旋都是以新增節點N為支點不是P。這裡将N節點的兩個NIL節點命名為X、L。如下:
至于左内側則處理邏輯如下:先進行右旋,然後左旋,最後着色。
ConcurrentHashMap 的treeifyBin過程
ConcurrentHashMap的連結清單轉換為紅黑樹過程就是一個紅黑樹增加節點的過程。在put過程中,如果發現連結清單結構中的元素超過了TREEIFY_THRESHOLD(預設為8),則會把連結清單轉換為紅黑樹:
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i); treeifyBin主要的功能就是把連結清單所有的節點Node轉換為TreeNode節點,如下:
private final void treeifyBin(Node<K,V>[] tab, int index) {
Node<K,V> b; int n, sc;
if (tab != null) {
if ((n = tab.length) < MIN_TREEIFY_CAPACITY)
tryPresize(n << 1);
else if ((b = tabAt(tab, index)) != null && b.hash >= 0) {
synchronized (b) {
if (tabAt(tab, index) == b) {
TreeNode<K,V> hd = null, tl = null;
for (Node<K,V> e = b; e != null; e = e.next) {
TreeNode<K,V> p =
new TreeNode<K,V>(e.hash, e.key, e.val,
null, null);
if ((p.prev = tl) == null)
hd = p;
else
tl.next = p;
tl = p;
}
setTabAt(tab, index, new TreeBin<K,V>(hd));
}
}
}
}
} 先判斷目前Node的數組長度是否小于MIN_TREEIFY_CAPACITY(64),如果小于則調用tryPresize擴容處理以緩解單個連結清單元素過大的性能問題。否則則将Node節點的連結清單轉換為TreeNode的節點連結清單,建構完成之後調用setTabAt()建構紅黑樹。TreeNode繼承Node,如下:
static final class TreeNode<K,V> extends Node<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node<K,V> next,
TreeNode<K,V> parent) {
super(hash, key, val, next);
this.parent = parent;
}
......
} 我們以下面一個連結清單作為案例,結合源代碼來分析ConcurrentHashMap建立紅黑樹的過程:
12
12作為跟節點,直接為将紅程式設計黑即可,對應源碼:
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (r == null) {
x.parent = null;
x.red = false;
r = x;
} (【注】:為了友善起見,這裡省略NIL節點,後面也一樣)
1
此時根節點root不為空,則插入節點時需要找到合适的插入位置,源碼如下:
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = r;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
r = balanceInsertion(r, x);
break;
}
} 從上面可以看到起處理邏輯如下:
- 計算節點的hash值 p。dir 表示為往左移還是往右移。x 表示要插入的節點,p 表示帶比較的節點。
- 從根節點出發,計算比較節點p的的hash值 ph ,若ph > h ,則dir = -1 ,表示左移,取p = p.left。若p == null則插入,若 p != null,則繼續比較,直到直到一個合适的位置,最後調用balanceInsertion()方法調整紅黑樹結構。ph < h,右移。
- 如果ph = h,則表示節點“沖突”(和HashMap沖突一緻),那怎麼處理呢?首先調用comparableClassFor()方法判斷節點的key是否實作了Comparable接口,如果kc != null ,則通過compareComparables()方法通過compareTo()比較帶下,如果還是傳回 0,即dir == 0,則調用tieBreakOrder()方法來比較了。tieBreakOrder如下:
static int tieBreakOrder(Object a, Object b) {
int d;
if (a == null || b == null ||
(d = a.getClass().getName().
compareTo(b.getClass().getName())) == 0)
d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
-1 : 1);
return d;
} tieBreakOrder()方法最終還是通過調用System.identityHashCode()方法來比較。
确定插入位置後,插入,由于插入的節點有可能會打破紅黑樹的結構,是以插入後調用balanceInsertion()方法來調整紅黑樹結構。
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true; // 所有節點預設插入為紅
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// x.parent == null,為跟節點,置黑即可
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// x 父節點為黑色,或者x 的祖父節點為空,直接插入傳回
else if (!xp.red || (xpp = xp.parent) == null)
return root;
/*
* x 的 父節點為紅色
* ---------------------
* x 的 父節點 為 其祖父節點的左子節點
*/
if (xp == (xppl = xpp.left)) {
/*
* x的叔父節點存在,且為紅色,顔色交換即可
* x的父節點、叔父節點變為黑色,祖父節點變為紅色
*/
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
/*
* x 為 其父節點的右子節點,則為内側插入
* 則先左旋,然後右旋
*/
if (x == xp.right) {
// 左旋
root = rotateLeft(root, x = xp);
// 左旋之後x則會變成xp的父節點
xpp = (xp = x.parent) == null ? null : xp.parent;
}
/**
* 這裡有兩部分。
* 第一部分:x 原本就是其父節點的左子節點,則為外側插入,右旋即可
* 第二部分:内側插入後,先進行左旋,然後右旋
*/
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
/**
* 與上相對應
*/
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
} 回到節點1,其父節點為黑色,即:
else if (!xp.red || (xpp = xp.parent) == null)
return root; 直接插入:
9
9作為1的右子節點插入,但是存在紅紅沖突,此時9的并沒有叔父節點。9的父節點1為12的左子節點,9為其父節點1的右子節點,是以處理邏輯是先左旋,然後右旋,對應代碼如下:
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
圖例變化如下:
2
節點2 作為1 的右子節點插入,紅紅沖突,切其叔父節點為紅色,直接變色即可,:
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
} 對應圖例為:
節點0作為1的左子節點插入,由于其父節點為黑色,不會插入後不會打破紅黑樹結構,直接插入即可:
11
節點11作為12的左子節點,其父節點12為黑色,和0一樣道理,直接插入:
7
節點7作為2右子節點插入,紅紅沖突,其叔父節點0為紅色,變色即可:
19
節點19作為節點12的右子節點,直接插入:
至此,整個過程已經完成了,最終結果如下: