簡介
快速排序也采用的是分而制之的思想。那麼快速排序和歸并排序的差別在什麼地方呢?
歸并排序是将所有的元素拆分成一個個排好序的數組,然後将這些數組再進行合并。
而快速排序雖然也是拆分,但是拆分之後的操作是從數組中選出一個中間節點,然後将數組分成兩部分。
左邊的部分小于中間節點,右邊的部分大于中間節點。
然後再分别處理左邊的數組合右邊的數組。
快速排序的例子
假如我們有一個數組:29,10,14,37,20,25,44,15,怎麼對它進行快速排序呢?
先看一個動畫:
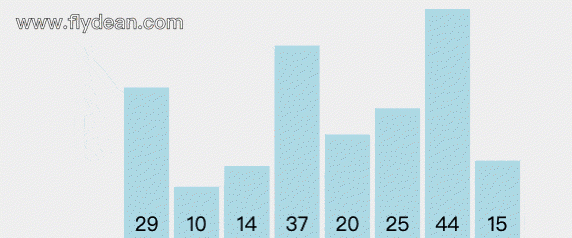
我們再分析一下快速排序的步驟。
我們選擇的是最左邊的元素29作為中間點元素,然後将數組分成三部分:[0, 14, 15, 20, 25],[29],[44, 37]。
中間節點29已經排好序了,不需要處理。
接下來我們再對左右分别進行快速排序。最後就得到了一個所有元素都排序的數組。
快速排序的java代碼實作
我們先來看最核心的部分partition,如何将數組以中間節點為界,分成左右兩部分呢?
我們的最終結果,是要将array分割成為三部分。
首先我們選擇最左側的元素作為中間節點的值。然後周遊數組中的其他元素。
假如m=middleIndex,k=要周遊的元素index
考慮兩種情況,第一種情況是數組中的元素比中間節點的值要大。
這種情況下,m不需要移動,k+1繼續周遊即可。
第二種情況下,數組中的元素比中間節點的值要小。
因為m左邊的元素都要比中間節點的值要小,是以這種情況下m需要+1,即右移一位。
現在m+1位置的元素要麼還沒有進行比較,要麼就是比中間節點的值要大,我們可以巧妙的将m+1位置的元素和k位置的元素互換位置,這樣仍然能夠保證m左側的元素要比中間節點的值要小。
将上面的分析總結成java代碼如下:
private int partition(int[] array, int i, int j) {
//選擇最左側的元素作為中心點,middleValue就是中心點的值
int middleValue = array[i];
int middleIndex = i;
//從i+1周遊整個數組
for (int k = i+1; k <= j; k++) {
//如果數組元素小于middleValue,表示middleIndex需要右移一位
//右移之後,我們需要将小于middleValue的array[k]移動到middleIndex的左邊,
// 最簡單的辦法就是交換k和middleIndex的值
if (array[k] < middleValue) {
middleIndex++;
//交換數組的兩個元素
swap(array, k , middleIndex);
} //如果數組元素大于等于middleValue,則繼續向後周遊,middleIndex值不變
}
// 最後将中心點放入middleIndex位置
swap(array, i, middleIndex);
return middleIndex;
} 最後我們需要将最左側的元素和中間節點應該在的index的元素互換下位置,這樣就将中間節點移動到了中間位置,并傳回中間位置。
再來看下divide的代碼:
public void doQuickSort(int[] array, int low, int high) {
//遞歸的結束條件
if (low < high) {
//找出中心節點的值
int middleIndex = partition(array, low, high);
//數組分成了三部分:
// a[low..high] ~> a[low..m–1], pivot, a[m+1..high]
//遞歸周遊左側部分
doQuickSort(array, low, middleIndex-1);
// a[m] 是中心節點,已經排好序了,不需要繼續周遊
//遞歸周遊右側部分
doQuickSort(array, middleIndex+1, high);
log.info("QuickSort之後的數組:{}",array);
}
} divide的代碼就很簡單了,找到中間節點的位置之後,我們再分别周遊數組的左右兩邊即可。最後得到排好序的數組。
随機快速排序的java實作
上面的例子中,我們的中間節點的選擇是數組的最左元素,為了保證排序的效率,我們可以從數組中随機選擇一個元素來作為中間節點。
private int partition(int[] array, int i, int j) {
//随機選擇一個元素作為中心點,middleValue就是中心點的值
int randomIndex=i+new Random().nextInt(j-i);
log.info("randomIndex:{}",randomIndex);
//首先将randomIndex的值和i互換位置,就可以複用QuickSort的邏輯
swap(array, i , randomIndex);
int middleValue = array[i];
int middleIndex = i;
//從i周遊整個數組
for (int k = i+1; k <= j; k++) {
//如果數組元素小于middleValue,表示middleIndex需要右移一位
//右移之後,我們需要将小于middleValue的array[k]移動到middleIndex的左邊,
// 最簡單的辦法就是交換k和middleIndex的值
if (array[k] < middleValue) {
middleIndex++;
//交換數組的兩個元素
swap(array, k , middleIndex);
} //如果數組元素大于等于middleValue,則繼續向後周遊,middleIndex值不變
}
// 最後将中心點放入middleIndex位置
swap(array, i, middleIndex);
return middleIndex;
} 上面的代碼,我們在分區的時候,先選擇出一個随機的節點,然後将這個随機的節點和最左側的元素交換位置,後面的代碼就可以重用上面的QuickSort的代碼邏輯了。
快速排序的時間複雜度
從上面的分析我們可以看出,每次分區的時間複雜度應該是O(N),而divide又近似二分法,是以總的時間複雜度是O(N logN)。
本文的代碼位址:
learn-algorithm本文作者:flydean程式那些事
本文連結:
http://www.flydean.com/algorithm-quick-sort/本文來源:flydean的部落格
歡迎關注我的公衆号:程式那些事,更多精彩等着您!