四元數基礎知識。
四元數基礎
以下内容摘自《3D數學基礎:圖形與遊戲開發》(清華大學出版社)
四元數
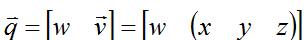
1.四元數和軸-角對
繞軸n旋轉θ角:n是一個向量,根據左手或右手法則定義旋轉的正方向, θ角表示旋轉的量。
那麼表示這個旋轉的四元數為:
2.機關四元數
幾何上存在兩個機關四元數,它們代表沒有角位移:
任意四元數乘以一個幾何機關四元數得到的角位移相同(雖然乘以兩種形式得到q和-q的數形式不同,但是幾何意義相同,可以認為結果相同)。
數學上實際隻有一個機關四元數,即:
因為數學上q和-q不相等。
3.四元數的模
代入軸-角對的公式求模。
n為機關向量,最後可以得到四元數的模為1.稱為機關四元數。
4.四元數的共轭和逆
四元數的共轭就是讓四元數的向量部分取負,記作:
四元數和它的共轭代表相反的角位移,因為相當于旋轉軸反向。
四元數的逆定義為四元數的共轭除以它的模:
一般使用機關四元數,此時它的逆和共轭其實是相等的。
5.四元數乘法(叉乘)
不用為四元數叉乘使用乘号,“行”“列”四元數也沒有什麼差別。
四元數叉乘滿足結合律,但是不滿足交換律。
四元數乘積的模等于模的乘積,這樣保證了機關四元數相乘仍然是機關四元數。
四元數乘積的逆等于各個四元數的逆以相反的順序相乘。
6.标準3D點的四元數旋轉
擴充一個标準的3D點(x,y,z)到四元數空間,通過定義四元數:
即可。
設我們讨論的旋轉四元數為:
則執行下面的乘法可以使3D點p繞n旋轉:
多次旋轉的情況:
注意這個旋轉是以從右向左的順序發生的。
可以改變标準的定義,以相反的運算順序來定義四元數乘法,進而将形式變為與旋轉發生的順序一緻,此處公式略去。
7.四元數“差”
利用四元數的乘法和逆,可以計算兩個四元數的“差”,四元數“差”表示一個方位到另一個方位的角位移。
注意不能除以四元數,隻能乘以它們的逆來達到目的。
8.四元數的點乘
點乘結果是标量,兩個機關四元數點乘的結果區間為[-1,1]。
點乘結果的絕對值越大,相乘的兩個四元數代表的角位移越相似。
9.四元數的對數、指數和标量乘運算
略。
10.四元數求幂 
四元數基礎
若四元數
代表一個角位移,
中取t等于1/3,就得到代表1/3這個角位移的四元數。
注意的是四元數表達角位移時使用最短圓弧,不能繞圈。
即如果q代表繞x軸順時針旋轉60°,那麼t取4時不是預期的繞x軸順時針旋轉240°,而是逆時針80°。
是以凡是涉及到指數運算的代數公式,如
,對四元數不再适用。
S=4,t=1/2,本來應該是等同于
,然而由于t=4時選了最短弧,是以産生的不是預期的結果。
11.四元數插值——“Slerp”
球面線性插值(Spherical Linear Interpolation).
Slerp運算非常有用,因為它可以在兩個四元數間平滑插值,避免了歐拉角插值的所有問題(角度限制以找到最短弧,萬向鎖(導緻抖動、路徑錯誤),根本問題是插值過程中角速度不是恒定的。)
兩個标量間的插值一般是這樣:
可以使用同樣的步驟在四元數間插值:
(1).計算兩個值的差。利用逆矩陣推到的。
(2).計算差的一部分。(四元數求幂)。
(3).在開始值上加上差的一部分。(方法使用四元數乘法來組合角位移)
這是理論上的Slerp計算過程。實踐中将使用一種更加有效的方法。
所有機關四元數都存在于一個4D球面上。
幾何推導略。結果:
可以用點乘來計算兩個四元數之間的“角度”。
有兩點需要考慮:
(1)四元數q和-q代表相同的方位,但它們作為slerp的參數時可能導緻不一樣的結果。解決方法是選擇兩個數的符号使得它們點乘的結果是非負。
(2)如果兩個四元數非常接近,那麼sin會非常小,這時候除法可能會出現問題,為了避免這樣的問題,當sin非常小時使用簡單的線性插值。
12.四元數樣條——“squad”
Spherical and Quadrangle
木有看懂。
13.四元數的優缺點
優點:
平滑插值。
快速連接配接和角位移求逆。
能和矩陣形式快速轉換。
僅用四個數。
缺點:
比歐拉角稍微大一些。
四元數可能不合法。壞的輸入資料或浮點數舍入誤差積累引起。(通過四元數标準化解決這個問題,確定四元數為機關大小。)
難于使用。
14.四元數、歐拉角、矩陣之間的轉換
參考資料:
《3D數學基礎:圖形與遊戲開發》(清華大學出版社)
作者: 聖騎士Wind
出處: 部落格園: 聖騎士Wind
Github: https://github.com/mengdd
微信公衆号: 聖騎士Wind