前面幾篇文章介紹了線性回歸算法,他們都屬于線性模型現在這篇說的是邏輯回歸,雖然都有回歸二字卻是非線性模型;邏輯回歸的輸出為特定離散值,用于判定資料的分類是以 邏輯回歸(Logistic regression) 也稱為分類模型;分類模型又有二分與多分類,邏輯回歸通常用于二分類;以下内容為Standard機器學習課程的總結記錄;
邏輯回歸的應用場景有:
1、是否為垃圾郵件
2、是否患病
3、是否金融詐騙
4、是否為虛假賬号
除了上述這些場景外還有很多類似的預測、判别場景;
與前面講的線性回歸算法類似,編寫邏輯回歸的步驟為:
1、編寫預測函數
2、編寫損失函數
3、求得使損失函數最小的回歸參數w
預測函數
預測函數其實就是模型,邏輯回歸利用了Sigmoid函數來輸出0-1範圍的連續值,是以邏輯函數又稱為S函數:
S函數公式如下:
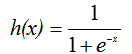
公式輸出為以下S型的圖形,是以Sigmoid稱為S函數:
和線性回歸一樣邏輯回歸模型也一樣有參數與特征這裡用x表示為特征、w為參數,是以邏輯回歸模型為:
模型的輸出為連續值,但是我們的想要的分類結果卻是離散的是以需要把值映射為0、1;通過上面S函數的圖形我們可以看出當x>=0時h(x)>=0.5,x<0時h(x)<0.5,通常情況下當h(x)>=0.5時我們把模型輸出分為1分類,h(x)<0.5時為0分類; 從這裡可以看出y=0 + Y=1的機率為1,是以有:
損失函數
線性回歸中有講過損失函數是用于求得預測值與實際值差距的函數,邏輯回歸也一樣使用損失函數求得預測值與實際值的最小值此時的預測函數參數為模型的最佳參數; 與線性回歸中有差別的是,線上性回歸模型中我們使用的是平方損失函數,而這裡我們将使用對數損失函數;
假設樣本符合伯努利分布然後通過機率形式表示,通過最大似然估計推導得出的;由于這裡說的是二進制分類是以邏輯回歸的損失函數為:
求得損失函數的最小值
通過前面所講的梯度下降法可以求出上面所說的損失函數最小值; 求L(w)最小值:
求關于w的偏導數可以得出:
設α為步長,n為w向量大小,m為資料集大小,求w最小值的疊代過程為:
參考資料:
https://en.wikipedia.org/wiki/Logistic_function
Standard機器學習
文章首發位址:Solinx
http://www.solinx.co/archives/880