基礎算法——排序【一】

排序可以說時最基礎的算法之一，排序就是将資料按照某種邏輯重新排列的過程，比如從大到小排序、從小到大排序；排序非常常見比如有購物車物品的排序、曆史訂單的排序等等；算法我們比較關心的主要有兩點：時間複雜度與空間複雜度，排序算法一樣；這篇文章隻介紹幾種基本的排序算法：冒泡排序、插入排序、選擇排序；

選擇排序

　　算法邏輯上分為已排序未排序兩個區間，從目前清單中選擇最小的元素與目前清單第一個元素交換位置，從清單剩餘元素中找到最小元素與清單第二個元素交換位置如此重複執行的算法為選擇排序算法；

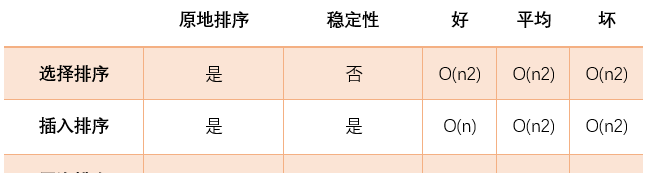
　　選擇排序與資料的初始狀态無關，每次查找最小元素值時都會與數組中元素進行交換位置，是以選擇排序為非穩定排序算法，在各種情況下算法時間複雜度都為O(n2)，空間複雜度為O(n)；

func SelectionSort(data [] int) {
     n := len(data)
     if n <= 1 {
         return
     }
     for i := 0; i < n; i++ {
         //最小元素索引
         min := i
         for j := i + 1; j < n; j++ {
             if data[j] < data[min] {
                 min = j
             }
         }
         //交換元素，交換後未已排序資料
         data[i], data[min] = data[min], data[i]
     }
 }
           

插入排序

　　與選擇排序類似在邏輯上清單分為已排序和未排序兩個區間，初始時已排序區間未為左邊第一個元素，插入排序的核心為從右邊未排序區間中選擇元素插入到左邊合适的位置，直到已排序清單長度等于原始清單長度；插入排序算法的關鍵步驟為元素比較與元素的移動，當從未排序端拿資料插入到已排序端時已排序端可能會存在大量的資料移動；

　　與選擇排序不同的是清單初始狀态對插入排序的性能影響很大，當清單初始狀态有序度很高時插入排序并不需要大量移動資料，從中可以看出插入排序為原地排序算法、算法是穩定的；

　　算法最好情況下時間複雜度為：O(n)、平均、最壞複雜度為：O(n2)；

func InsertionSort(data [] int) {
          n := len(data)
          for i := 1; i < n; i++ {
              value := data[i]
              //查找插入位置
              var j int
              for j = i - 1; j >= 0; j-- {
                  if data[j] > value {
                      //資料後移
                      data[j+1] = data[j]
                  } else {
                      break
                  }
              }
              data[j+1] = value
          }
 }
           

冒泡排序

　　每次比較相鄰兩個元素是否滿足，否則交換相鄰兩個元素，每次冒泡至少一個元素移動到它所屬位置，重複N次完成清單排序；

　　冒泡操作核心為項鍊元素交換，空間複雜度為O(1)，為原地排序算法；算法是穩定的，最好情況時間複雜度為為O(n)，平均與最壞情況時間複雜度為：O(n2)；

func BubbleSort(data [] int) {
     n := len(data)
     for i := 0; i < n; i++ {
         //是否有資料交換，用于當某輪中資料已排序時退出循環
         flag := false
         for j := 0; j < n-1-i; j++ {
             if data[j] > data[j+1] {
                 //冒泡
                 data[j], data[j+1] = data[j+1], data[j]
                 flag = true
             }
         }
         if !flag {
             break
         }
     }
      }
           

基礎排序算法特性

參考資料： 《算法四》