雲栖号資訊:【 點選檢視更多行業資訊】
在這裡您可以找到不同行業的第一手的上雲資訊,還在等什麼,快來!
摘要:遞歸是一種應用非常廣泛的算法(或者程式設計技巧)。之後我們要講的很多資料結構和算法的編碼實作都要用到遞歸,比如 DFS 深度優先搜尋、前中後序二叉樹周遊等等。是以,搞懂遞歸非常重要,否則,後面複雜一些的資料結構和算法學起來就會比較吃力
推薦使用者注冊領取傭金很多人都遇到過,很多 App 在推廣的時候都是這個套路。「蕭何」引薦「韓信」加入劉邦陣營,「韓信」又引薦了那些年上鋪的兄弟「韓大膽」加入。我們就可以認為「韓大膽」的最終推薦人是「蕭何」,「韓信」的最終推薦人是「蕭何」,而「蕭何」沒有最終推薦人。
用資料庫記錄他們之間的關系,soldier_id 表示士兵 id,referrer_id 表示推薦人 id。
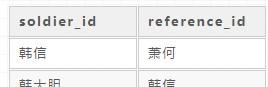
那麼問題來了,「給定一個士兵 id,如何查找這個使用者的「最終推薦人」」,帶着這個問題,我們正式進入遞歸。
遞歸三要素
有兩個最難了解的知識點,一個是 「動态規劃」,「一個是遞歸」。
大學軍訓,都會經曆過排隊報數,報數過程中自己開小差看見了一個漂亮國小姐,不知道旁邊的哥們剛說的數字,是以再問一下左邊哥們剛報了多少,隻要在他說的數字 + 1 就知道自己樹第幾個了,關鍵是現在你旁邊的哥們 看見漂亮國小姐竟然忘記剛剛自己說的數字了,也要繼續問他左邊的老鐵,就這樣一直往前問,直到第一個報數的孩子,然後一層層把數字傳遞到自己。
這就是一個非常标準的遞歸求解過程,問的過程叫「遞」,回來的過程交「歸」。轉換成遞推公式:
- f(n)=f(n-1) + 1, 存在 f(1) = 1
- f(n) 表示自己的數字,f(n - 1) 表示前面一個人的報數,f(1) 表示第一個人知道自己是第一個報的數字。
根據遞推公式,很容易的轉換成遞歸代碼:
到底什麼問題可以用遞歸解決呢?總結了三個必要元素,隻要滿足一下三個條件,就可以使用遞歸解決。
1.一個問題可以分解多個子問題
就是可以分解恒數字規模更小的問題,比如要知道自己的報數,可以分解『前一個人的報數』這樣的子問題。
2.問題本身與分解後的子問題,除了資料規模不同,求解算法相同
『求解自己的報數』和前面一個人『求解自己的報數』思路是一模一樣。
3.存在遞歸終止條件
問題分解成子問題的過程中,不能出現無限循環,是以需要一個終止條件,就像第一排或者其中任何一個知道自己報數的孩子不需要再詢問上一個人的數字,f(1) = 1 就是遞歸終止條件。
如何編寫遞歸代碼
其實最關鍵的就是 「寫出遞推公式,找到終止條件」,然後把遞推公式轉成 代碼就容易多了。
再舉一個「青蛙跳台階」的算法問題,假設有 n 個台階,每次可以跳 1 個或者 2 個台階,走這 n 個台階有多少種走法?
再仔細想想,實際上,根據第一步的走法可以把所有的走法分兩類,第一類是第一步走了 1 個台階,另一種是第一步走了 2 個台階。是以 n 個台階的走法就等于先走 1 階後, n-1 個台階的走法 + 先走 2 階後, n-2 個台階的走法。
繼續分析終止條件,當隻有一個台階的時候不需要再繼續遞歸,f (1) = 1。似乎還不夠,假如有兩個台階呢?分别用 n = 2、n=3 驗證下。f(2) = 2 也是終止條件之一。
是以該遞歸的終止條件就是 f(1) = 1,f(2) = 2。
根據公式轉成代碼則是
劃重點了:「寫遞歸大媽的關鍵就是找到如何将大問題分解成小問題的規律,并且基于此寫出遞推公式,再推出終止條件,租後将地推公式和終止條件翻譯成代碼。」
對于遞歸代碼,我們不要試圖去弄清楚整個遞和歸的問題,這個不适合我們的正常思維,我們大腦更适合平鋪直叙的思維,當看到遞歸切勿妄想把遞歸過程平鋪展開,否則會陷入一層一層往下調用的循環。
「當遇到一個問題 1 可以分解若幹個 2,3,4 問題,我們隻要假設 2,3,4 已經解決,在此基礎上思考如何解決 A。這樣就容易多了。」
是以當遇到遞歸,編寫 代碼的關鍵就是 「把問題抽象成一個遞推公式,不要想一層層的調用關系,找到終止條件。」
防止棧溢出
遞歸最大的問題就是要防止棧溢出以及死循環。為何遞歸容易造成棧溢出呢?我們回想下之前說過的棧資料結構,不清楚的朋友可以翻閱曆史文章。函數調用會使用棧來儲存臨時變量,每次調用一個函數都會把臨時變量封裝成棧幀壓入線程對應的棧中,等方法結束傳回時,才出棧。如果遞歸的資料規模比較大,調用層次很深就會導緻一直壓入棧,而棧的大小通常不會很大就會導緻堆棧溢出的情況。
如何防止呢?
我們隻能在代碼裡面限制最大深度,直接傳回錯誤,使用一個全局變量表示遞歸的深度,每次執行都 + 1,當超過指定門檻值還沒有結束的時候直接傳回錯誤。
警惕重複計算
青蛙跳台階的問題就有重複計算的問題,我們試着把遞歸過程分解下,想要計算 f(5),需要先計算 f(4) 和 f(3),而計算 f(4) 還需要計算 f(3),是以,f(3) 就被計算了很多次,這就是重複計算問題。為了避免重複計算,我們可以通過一個資料結構(比如 HashMap)來儲存已經求解過的 f(k)。當遞歸調用到 f(k) 時,先看下是否已經求解過了。如果是,則直接從散清單中取值傳回,不需要重複計算,這樣就能避免剛講的問題了。
遞歸的空間複雜度因為每次調用都會在棧上儲存一次臨時變量,是以它的空間複雜度就是 O(N),而不是 O(1)。
如何将遞歸轉換成非遞歸代碼
遞歸有利有弊,遞歸寫起來很簡潔,而不好的地方就是空間複雜度是 O(n),有堆棧溢出風險,存在重複計算。要根具體情況來選擇是否需要遞歸。
還是軍訓排隊報數的例子,如何變成非遞歸。
f(n) = f(n-1) +1;
對于台階問題也是可以改成循環實作。
尋找最佳推薦人
現在遞歸說完了,我們如何解答開篇的問題:根據士兵 id 找到最佳推薦人?
遞歸是一種非常高效、簡潔的編碼技巧。隻要是滿足“三個條件”的問題就可以通過遞歸代碼來解決。
不過遞歸代碼也比較難寫、難了解。編寫遞歸代碼的關鍵就是不要把自己繞進去,正确姿勢是寫出遞推公式,找出終止條件,然後再翻譯成遞歸代碼。
遞歸代碼雖然簡潔高效,但是,遞歸代碼也有很多弊端。比如,堆棧溢出、重複計算、函數調用耗時多、空間複雜度高等,是以,在編寫遞歸代碼的時候,一定要控制好這些副作用。
【雲栖号線上課堂】每天都有産品技術專家分享!
課程位址:
https://yqh.aliyun.com/live立即加入社群,與專家面對面,及時了解課程最新動态!
【雲栖号線上課堂 社群】
https://c.tb.cn/F3.Z8gvnK
原文釋出時間:2020-05-18
本文作者:碼哥位元組
本文來自:“
掘金”,了解相關資訊可以關注“掘金”