雲栖号資訊:【 點選檢視更多行業資訊】
在這裡您可以找到不同行業的第一手的上雲資訊,還在等什麼,快來!
這個算法挺冷門的,至少比Apriori算法冷門。很多資料挖掘的教材還會提一提Apriori,但是提到FP-growth的相對要少很多。原因也簡單,因為從功能的角度上來說,FP-growth和Apriori基本一樣,相當于Apriori的性能優化版本。
但不得不說有時候優化是一件很尴尬的事,因為優化意味着性能要求很高。但是反過來說,對于性能有着更高要求的應用場景,無論是企業也好,還是學術研究也罷,現在早就有了更好的選擇,完全可以用更強大的算法和模型,沒必要用這麼個古老算法的優化版。對于那些性能要求不高的場景,簡單的Apriori也就夠了,優化的必要也不是很大。
但是不管這個算法命運如何,至少從原理和思路理念上來說的确有為人稱道的部分。下面我們就來看看它的具體原理吧。
FP-growth與FP-tree
FP-growth的核心價值在于加速,在之前介紹的Apriori算法當中,我們每一次從候選集當中篩選出頻繁項集的時候,都需要掃描一遍全量的資料庫來計算支援度,顯然這個開銷是很大的,尤其是我們資料量很大的時候。
FP-growth的精髓是建構一棵FP-tree,它隻會掃描完整的資料集兩次,是以整體運作的速度顯然會比Apriori快得多。之是以能做到這麼快,是因為FP-growth算法對于資料的挖掘并不是針對全量資料集的,而隻針對FP-tree上的資料,是以這樣可以省略掉很大一部分資料,進而節省下許多計算資源。
從這裡我們可以看出,FP-tree是整個算法的精髓。在我們介紹整個樹的建構方法以及一些細節之前,我們先來看下FP這兩個字母的含義。相信很多同學從一開始的時候就開始迷惑了,其實FP這兩個字母是frequent pattern的縮寫,翻譯過來是頻繁模式,其實也可以了解成頻繁項,說白了,FP-tree這棵樹上隻會存儲頻繁項的資料,我們每次挖掘頻繁項集和關聯規則都是基于FP-tree,這也就過濾了不頻繁的資料。
這是一棵生成好的FP-tree,我們先來看一下它的樣子,再來詳細解讀其中的細節和原理。
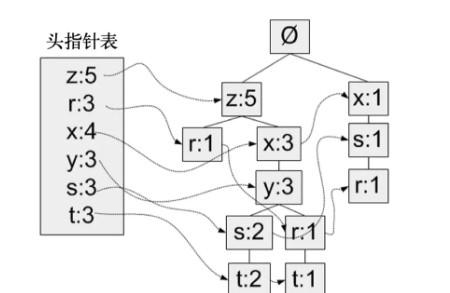
頭指針表
上圖這個結構初看會覺得很混亂,完全不知道應該怎麼了解。這是很正常的,但如果我們把上圖拆開,可以分成兩個部分,左邊的部分是一個連結清單,右邊是一棵樹。隻不過左邊的連結清單指到了右邊的樹上,是以整體看起來有些複雜。
我們先忽略右側的樹的部分,以及指針表和樹之間關聯的指針,單純地來看一下左側的頭指針表。僅僅看這一部分就簡單多了,它其實是一個單頻繁項的集合。
前面我們提到我們在使用FP-growth算法的過程當中,一共隻需要周遊兩次資料集。其中第一次周遊資料集就在這裡,我們首先周遊了一遍資料集,求出了所有元素出現的次數。然後根據門檻值過濾掉不頻繁的元素,保留下來的結果就是單個頻繁項的集合。
這裡的邏輯非常簡單,隻有兩件事,第一件事是統計每個單獨的項出現的次數,第二件事是根據門檻值将不頻繁的項過濾掉。
通過這個方法,我們就生成了頭指針表裡的資料。之後我們要在建立FP-tree的過程當中将這份資料轉化成連結清單,也就是左邊的頭指針表。雖然我們還不了解建樹的原理,但至少我們可以把dict轉化成指針表,這個邏輯非常簡單,說白了我們隻需要在dict的value當中增加一個引用即可。
這裡的None要存的就是連結清單下一個位置的引用,隻是目前我們隻有連結清單頭,是以全部設定為None。
建立FP-tree
我們有了頭指針表的資料,也就是高頻的單個元素的資料之後,顯然要将它用起來。很明顯,我們可以用它來過濾整個資料集,過濾掉其中低頻的元素。
其實本質上來說FP-tree的建構過程,其實就是一個将過濾之後的結果插入到樹上的過程。後面的事情後面再說,我們首先來看過濾。
單純的過濾當然非常簡單,我們隻需要判斷資料集中的元素是否在頭指針表中出現即可。但是不僅如此,由于我們之後想要将它插入到樹中。
這裡利用了huffman樹的思想,我們希望頻次越高的元素存放的位置距離根節點越近。頻次越低的離根節點越遠,進而優化我們查詢的效率。要做到這點,需要我們對資料進行排序。
我們來實作這部分内容,這部分内容分為兩塊,第一塊是根據頭指針表進行過濾,第二塊是根據頭指針表中出現的頻次進行排序。
有了這份資料之後,我們距離建樹隻有一步之遙。FP-tree的建構剛才也提到過,非常簡單粗暴,就是将元素按照出現的頻次進行排序之後從樹根開始依次插入。在插入的過程當中,對路徑上的節點進行更新,我這麼說肯定很費解,但是看一張圖就肯定明白了:
一開始的時候樹為空,什麼也沒有,接着插入第一條資料{r, z}。由于z出現的次數大于r,是以先插入z再插入r,之後插入了一條{z,x,y,s,t},同樣是按照整體出現的頻次排序的。由于z已經插入了,是以我們将它出現的次數更新成2,之後發現沒有重複的元素,那麼就建構出一條新的分支。
本質上來說就是按照頻次排序之後,由淺到深依次插入,如果相同的元素之前已經出現過了,那麼就更新它出現的次數。
這個邏輯應該很好了解,在我們實作邏輯之前,我們先來建立樹節點的類。
這個類我們隻需要看代碼就好了,應該完全沒有難度,當然如果你願意你也可以給它加上一個可視化方法用來debug。但老實說樹結構單憑列印很難顯示得很清楚,是以我就不加了。
樹節點的定義寫好了之後,接下來就到了最重要的實作更新FP-tree的環節了。其實如果對上面的邏輯都了解了,這部分代碼也非常簡單,我們隻需要套用剛才的代碼将生成的資料按照順序插入進樹上即可。
這種在樹上傳入一個序列依次插入的做法非常常見,在很多資料結構當中有類似的操作,最經典的就是Trie樹了。如果你學過,會發現這個插入操作真的和Trie幾乎一模一樣,如果你沒學過,也沒有關系,這也不難了解。
更新頭指針表
FP-tree已經完成了,接下來我們要把更新頭指針表的邏輯加上,使得對于每一個項來說,我們都可以根據頭指針表找到這個元素在FP-tree上所有的位置。
我們仔細觀察一下上面的那張圖,我們選擇其中的一條鍊路進行高亮:
從上圖當中我們會發現,頭指針表的作用就是建立一個連結清單,将元素所有出現的位置全部串聯起來。
那麼什麼情況下我們需要向這個連結清單當中添加值呢?
稍微分析一下就會發現,其實就是我們在樹上建立新節點的時候。想通了這點就很簡單了,我們隻需要在上面的代碼當中增加幾行,使得在樹上建立新的節點的時候,用同樣的值更新一下頭指針連結清單。
這裡添加到末尾的操作,我們可以再建立一個dict來維護頭指針表的末尾節點,但我這裡偷懶了一下,就用最簡單的辦法,先周遊到連結清單的結尾,再進行添加:
通過FP-tree快速查找資料
現在,我們已經完整實作了FP-tree的建構,接下來就到了重頭戲,也就是頻繁項集的挖掘。我們有了這棵FP-tree之後應該怎麼用呢?
如果我們仔細觀察一下FP-tree的話,會發現這棵樹其實是資料的濃縮。可以認為是之前完整的資料集去除了非頻繁的元素之後提煉得到的資料。根據APriori算法的原理,我們接下來要做的就是用長度為1的頻繁項集去建構長度為2的頻繁項集,以此類推,直到找出所有的頻繁項集為止。
但是在FP-growth算法當中,我們對這個邏輯稍稍做了一點點修正,我們每次固定一個元素,查找所有它構成的頻繁項集。我們要查找頻繁項集,首先需要擷取資料集,原始的資料包含了太多無關的資訊,我們已經用不到了,我們可以通過FP-tree高效地擷取我們需要的資料。
由于我們之前在插入FP-tree的時候,是嚴格按照元素出現的次數排序的,出現頻次高的元素放置的位置越高。這樣樹上某一個鍊路在資料集中出現的次數,就等于鍊路中最底層的節點的數字。
我們來看個例子:
紅框當中s的位置最低,是以整個鍊路上{z, x, y, s}在整個資料集當中出現的次數就是2,那麼我們确定了s之後,通過向上FP-tree,就可以還原出所有包含s的頻繁項構成的資料。
我們首先實作一個輔助方法,用來向上周遊整個鍊路所有的元素:
第二個輔助方法是固定某個元素之後,還原所有這個元素的資料。要還原所有資料,隻拿到一個節點是不夠的,我們需要知道這個元素在FP-tree上所有出現的位置。這個時候就需要用到頭指針表了,利用頭指針表,我們可以找到所有元素在FP-tree中的位置,我們隻需要調用上面的方法,就可以還原出資料集了。
這段邏輯同樣并不困難,其實就是周遊一個連結清單,然後再調用上面向上周遊樹的方法,擷取所有的資料。
遞歸建樹,挖掘頻繁項集
到這裡,我們對FP-tree應該有一個比較清晰的認識了,它的功能就是可以快速地查找某些元素組合的集合的頻次,因為相同元素構成的集合都被存儲在同一條樹鍊上了。
那麼我們怎麼根據FP-tree來挖掘頻繁項集呢?
這裡才是真正的算法的精髓。
我們還是看下上面的例子:
我們假設我們固定的元素是r,我們通過FP-tree可以快速找到和r共同出現的頻繁項有z,x,y,s。通過剛才上面的方法,我們可以得到一個新的必須包含r和頻繁項的新的資料集。我們把r從這份資料當中去除,然後對剩下的資料建構新的FP-tree,如果新的FP-tree當中還有其他元素,那麼這個元素必然可以和r構成二進制的頻繁項集。假設這個元素是x,那麼我們繼續重複上面的操作,再将x從資料中去除,再次建構FP-tree來挖掘包含x和r的三元頻繁項集,直到構成的FP-tree當中沒有元素了為止。
這就成了一個遞歸調用的過程,也就是說FP-tree本身并不能挖掘頻繁項集,隻能挖掘頻繁項。但是我們可以人為加上前提條件,當我們以必須包含x的資料為前提挖掘出來的頻繁項,其實就是包含x的二進制頻繁項集。我們加上的前提越來越多,也就是挖掘的頻繁項集的元素越來越多。
如果你還有點蒙,沒有關系,我們來看下代碼:
結尾
到這裡,整個FP-growth挖掘頻繁項集的算法就結束了,相比于Apriori,它的技術細節要多得多,如果初學者覺得不太好了解,這也是正常的,可以抓大放小,先從核心思路開始了解。
Apriori的核心思路是用兩個長度為l的頻繁項集去建構長度為l+1的頻繁項集,而FP-growth則稍有不同。它是将一個長度為l的頻繁項集作為前提,篩選出包含這個頻繁項集的資料集。用這個資料集建構新的FP-tree,從這個FP-tree當中尋找新的頻繁項。如果能找到,那麼說明它可以和長度為l的頻繁項集構成長度為l+1的頻繁項集。然後,我們就重複這個過程。
這個核心思路了解了,怎麼建構FP-tree,怎麼維護頭指針表都是很簡單的問題了。
【雲栖号線上課堂】每天都有産品技術專家分享!
課程位址:
https://yqh.aliyun.com/live立即加入社群,與專家面對面,及時了解課程最新動态!
【雲栖号線上課堂 社群】
https://c.tb.cn/F3.Z8gvnK
原文釋出時間:2020-05-15
本文作者:承志
本文來自:“
掘金”,了解相關資訊可以關注“掘金”