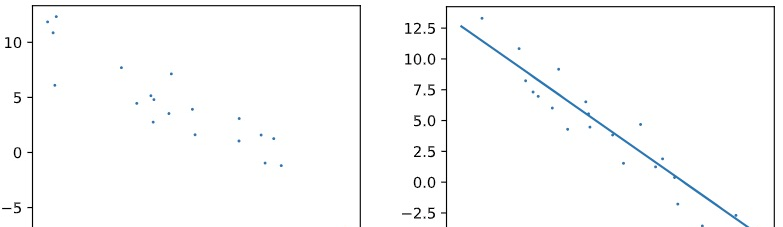
文章主要介紹了分類樹,下面我們再一起來看一下回歸樹,我們知道,分類決策樹的葉子節點即為分類的結果;同理,回歸樹的葉子節點便是連續的預測值。那麼,同樣是回歸算法,線性回歸和決策樹回歸有什麼差別呢?差別在于,前者拟合的是一條直線,而後者卻可以拟合非線性的資料,如下圖中的資料就是用線性回歸來拟合的:
當資料呈現非線性分布時,例如下面的資料,假設它統計了流行歌手的喜好程度和年齡的關系,該系數值在 10 歲之前很低,接着在 10 到 20 歲時達到最高,但随着年齡的增加,該興趣度會逐漸下降,如圖所示:
上面的資料如果用線性回歸來拟合,是這樣的:
很明顯,這樣做會得到較大的 Bias,那麼該資料就不應該使用線性回歸這種簡單的模型來表征,此時就需要用到非線性模型了,而回歸樹就是其中的一種。下邊左圖便是使用回歸樹對該資料進行拟合的結果,而右邊是這棵樹具體的樣子:當 age 小于等于 13 時,結果為 1.228;age 大于 31 時,結果是 0.41;age 在 (13, 21] 的區域,結果為 100,剩下區域的結果為 54。
下面我們具體看一下這棵回歸樹是如何建構的
建構回歸樹
首先,我們在整個樣本空間中選擇一個門檻值,該門檻值可以将樣本分為兩部分,接下來分别對這兩部分求出它們的均值,以均值作為預測值,計算所有資料的真實值到預測值之間的 SSR(Sum of Squared Residuals),SSR 本質上和 MSE(Mean Squared Error)的概念是一緻的,都是衡量整體預測值和真實值之間的差異的,該差異越小越好。
以本資料為例,剛開始我們選擇的門檻值 threshold 為 1,則下圖中的樣本被門檻值(虛線)分為兩部分,然後分别對左右兩邊的資料求平均,結果如圖中兩條水準實線所示,以水準線作為每個區域的預測值,接着我們對每個點,求它們離均值之間的差的平方(誤差的平方),并把它們加起來,得到的結果就是 SSR。
上圖中的 SSR 為
$$
SSR = (0-0)^2 + (0-35.8)^2 + ... + (0-35.8)^2 = 31358
每算完一個 SSR,都要改變門檻值,用同樣的方法在新的分類下算一個新的 SSR,如此循環下去,直到周遊完所有可能的域值,此時我們就可以作出一個「域值-SSR」的關系圖,如下:
以上過程的目的是為了找一個門檻值,可以使得 SSR 達到最小,而可以使 SSR 最小的域值就是我們的樹根。反過來了解一下,即我們需要在特征空間(定義域)找到一個值,該值把樣本分為兩類,分别對應了 2 個不同的預測結果,此預測結果和樣本真實值(值域)之間的差異要越小越好,在本例中,該值為 13,示意圖如下:
和分類樹一樣,隻要确定了樹根的建構算法,後面構造其他節點實際上和構造樹根是一模一樣的,以上圖為例,即分别以樹的左右兩邊的子樣本空間為整個樣本空間,繼續構造子樣本空間的“樹根”,實際上這就是遞歸,同時在遞歸的過程中,随着樹的節點不斷分裂,我們得到的殘差(SSR)會越來越小。
需要注意的是,決策樹如果不設限制,它的節點可以無限分裂下去,直到葉子節點中隻包含 1 個元素為止,此時整棵樹的殘差達到最小值 0,這樣做會讓我們的模型在訓練時得到很低的 Bias,但可想而知的是它的泛化能力很弱,即 Variance 很高,于是便過拟合了,這也是決策樹容易過拟合的原因。
為了防止過拟合,通常有 2 個參數可以設定,一個是樹的高度,另一個是葉子節點中最小樣本的個數,本文中的模型對這兩個參數的設定分别是 3 和 4;在真實環境中,葉子節點的樣本數一般會設在 20 以上。
多元度特征的回歸樹
上面例子是使用單特征(年齡)來建構回歸樹,真實項目往往會有多個特征,此時我們該如何做呢?我們在原來的資料集中增加兩個特征:性别和月支出,如下
| 年齡 | 性别 | 月支出 | 流行歌手喜好度 |
|---|---|---|---|
| 3 | male | 300 | |
| 7 | female | 5 | |
| 13 | 500 | 90 | |
| 17 | 85 | ||
| 18 | 99 | ||
| 25 | 4000 | 75 | |
| 30 | 5000 | 40 | |
| 35 | 7000 |
現在我們知道了,構造決策樹的要點在于樹根的構造,多個特征的話,我們需要分别對每個特征,找出可以使 SSR 最低的門檻值,根據前面學到的知識,對年齡來說,可使 SSR 最低的域值是 「age<=7」,此時 $SSR_{age}=7137$;
同理,對月支出來說,可使 SSR 最低的域值是 「expense<=300」,此時 $SSR_{expense}=7143$。
而性别這個特征比較特别,它隻有一個門檻值,其 $SSR_{gender}=12287$。
以上三個數字,有興趣的同學可以根據上面的表格自己算一下,最終我們選擇 SSR 最低的特征及其門檻值作為根節點,即「age<=7」。
知道根節點如何産生後,後面節點的生成就好辦了,于是多元特征的回歸樹我們也建構出來了。
總結
本文主要介紹回歸決策樹的生成算法,及回歸樹中比較重要的參數為:樹的深度和葉子節點中最小的樣本數,這兩個參數可以防止過拟合問題。
最後我們一起學習了從多個特征次元來産生回歸樹,它和單次元特征的差別在于,每産生一個節點前,都需要計算每個特征的 $SSR_{min}$ 及其對應的門檻值,最後取其中最小的 $SSR_{min}$ 對應的特征和門檻值作為該節點。
參考資料:
Regression Trees, Clearly Explained相關文章: