資料結構與算法之美-9 二叉樹 紅黑樹 [MD]

博文位址

我的GitHub	我的部落格	我的微信	我的郵箱
baiqiantao		bqt20094	[email protected]

目錄

• 二叉樹
  • 23 | 二叉樹基礎（上）：什麼樣的二叉樹适合用數組來存儲？
    • 樹的相關概念
    • 二叉樹 Binary Tree
    • 如何存儲一棵二叉樹
      • 鍊式存儲法
      • 順序存儲法
    • 二叉樹的周遊(深度周遊)
  • 24 | 二叉樹基礎（下）：二叉查找樹
    • 二叉查找樹 Binary Search Tree
      • 查找操作
      • 插入操作
      • 删除操作
      • 其他操作：二叉排序樹
    • 支援重複資料的二叉查找樹
    • 時間複雜度分析
    • 解答開篇
• 紅黑樹
  • 25 | 紅黑樹（上）：為什麼工程中都用紅黑樹這種二叉樹？
    • 平衡二叉查找樹
    • 紅黑樹的定義
    • 為什麼說紅黑樹是“近似平衡”的？
    • 三種動态資料結構
  • 26 | 紅黑樹（下）：掌握這些技巧，你也可以實作一個紅黑樹
    • 實作紅黑樹的基本思想
    • 插入操作的平衡調整
    • 删除操作的平衡調整
      • 針對删除節點初步調整
      • 針對關注節點進行二次調整
    • 内容小結
• 遞歸樹
  • 27 | 遞歸樹：如何借助樹來求解遞歸算法的時間複雜度？
    • 歸并排序
    • 快速排序
    • 斐波那契數列
    • 全排列

前面講的都是

線性表

結構，棧、隊列等等。今天講的樹是一種

非線性表

結構，樹這種資料結構比線性表的資料結構要複雜得多，内容也比較多：

• 數、二叉樹
• 二叉查找樹
• 平衡二叉查找樹、紅黑樹

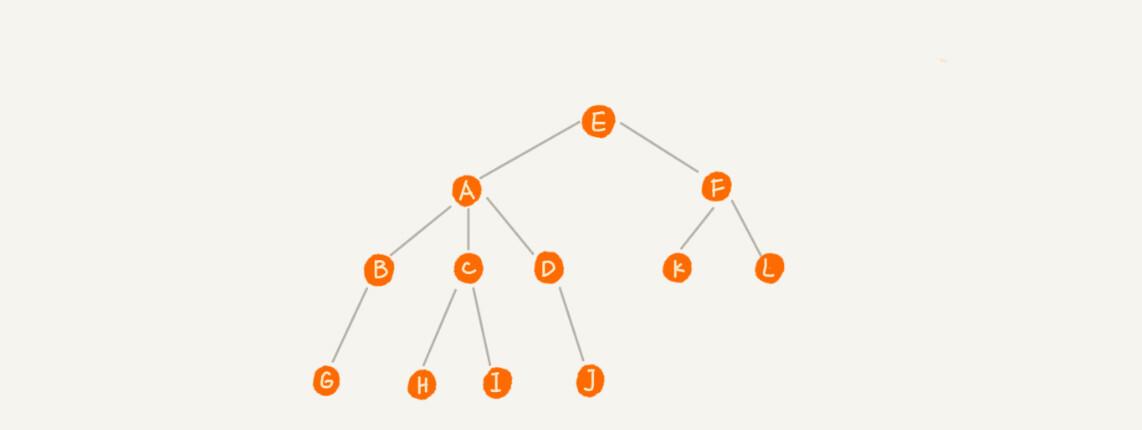
比如下面這幅圖，A 節點就是 B 節點的

父節點

，B 節點是 A 節點的

子節點

。B、C、D 這三個節點的父節點是同一個節點，是以它們之間互稱為

兄弟節點

。我們把沒有父節點的節點叫做

根節點

，也就是圖中的節點 E。我們把沒有子節點的節點叫做

葉子節點

，比如圖中的 G、H、I、J、K、L 都是葉子節點。

高度（Height）、深度（Depth）、層（Level）

• 在我們的生活中，

  高度

  這個概念就是

  從下往上

  度量，從最底層開始計數，并且計數的起點是 0。

• 深度

  這個概念在生活中是

  從上往下

  度量的，從根結點開始度量，并且計數起點也是 0。

• 層數

  跟深度的計算類似，不過，計數起點是 1，也就是說根節點位于第 1 層。

二叉樹，顧名思義，每個節點最多有兩個

叉

，也就是兩個子節點，分别是

左子節點

和

右子節點

。

上圖中，編号 2 的二叉樹中，

葉子節點全都在最底層

，除了葉子節點之外，每個節點都有左右兩個子節點，這種二叉樹就叫做

滿二叉樹

編号 3 的二叉樹中，

葉子節點都在最底下兩層

，

最後一層的葉子節點都靠左排列

，并且除了最後一層，

其他層的節點個數都要達到最大

，這種二叉樹叫做

完全二叉樹

每個節點有三個字段，其中一個存儲資料，另外兩個是指向左右子節點的指針。我們隻要拎住根節點，就可以通過左右子節點的指針，把整棵樹都串起來。

這種存儲方式我們比較常用，大部分二叉樹代碼都是通過這種結構來實作的。

我們把根節點 A 存儲在下标

i = 1

的位置，左子節點 B 存儲在下标

2 * i = 2

的位置，右子節點 C 存儲在

2 * i + 1 = 3

的位置。以此類推，B 節點的左子節點 D 存儲在

2 * i = 2 * 2 = 4

的位置，右子節點 E 存儲在

2 * i + 1 = 2 * 2 + 1 = 5

的位置。

總結一下，如果節點 X 存儲在數組中下标為 i 的位置，下标為

2 * i

的位置存儲的就是左子節點，下标為

2 * i + 1

的位置存儲的就是右子節點。反過來，下标為

i/2

的位置存儲就是它的父節點。通過這種方式，我們隻要知道根節點存儲的位置（一般情況下，為了友善計算子節點，根節點會存儲在下标為 1 的位置），這樣就可以通過下标計算，把整棵樹都串起來。

不過，剛剛舉的例子是一棵

完全二叉樹

(而非

滿二叉樹

)，是以僅僅浪費了一個下标為 0 的存儲位置。如果是

非完全二叉樹

，其實會浪費比較多的數組存儲空間。比如下面這個例子。

是以，如果某棵二叉樹是一棵完全二叉樹，那用數組存儲無疑是最節省記憶體的一種方式。因為數組的存儲方式并不需要像鍊式存儲法那樣，要存儲額外的左右子節點的指針。這也是為什麼完全二叉樹會單獨拎出來的原因，也是為什麼完全二叉樹要求

最後一層的子節點都靠左

的原因。

堆其實就是一種完全二叉樹，最常用的存儲方式就是數組。

前序周遊、中序周遊和後序周遊中的

前中後

，表示的是

節點

與它的

左右子樹節點

周遊列印的先後順序。

• 前序周遊

  是指，對于樹中的任意節點來說，先列印這個節點，然後再列印它的左子樹，最後列印它的右子樹

• 中序周遊

  是指，對于樹中的任意節點來說，先列印它的左子樹，然後再列印節點本身，最後列印它的右子樹

• 後序周遊

  是指，對于樹中的任意節點來說，先列印它的左子樹，然後再列印它的右子樹，最後列印節點本身

實際上，二叉樹的前、中、後序周遊就是一個

遞歸

的過程。比如，前序周遊，其實就是先列印根節點，然後再

遞歸

地列印左子樹，最後

遞歸

地列印右子樹。

寫遞歸代碼的關鍵，就是看能不能寫出

遞推公式

，而寫遞推公式的關鍵就是，如果要解決問題 A，就假設子問題 B、C 已經解決，然後再來看如何利用 B、C 來解決 A。是以，我們可以把前、中、後序周遊的遞推公式都寫出來。

前序周遊的遞推公式：preOrder(r) = print r -> preOrder(r->left) -> preOrder(r->right)
中序周遊的遞推公式：inOrder(r) = inOrder(r->left) -> print r -> inOrder(r->right)
後序周遊的遞推公式：postOrder(r) = postOrder(r->left) -> postOrder(r->right) -> print r
           

時間複雜度是

O(n)

二叉查找樹最大的特點就是，支援

動态資料集合

的快速

插入、删除、查找

操作。

我們之前說過，

散清單

也是支援這些操作的，并且散清單的這些操作比二叉查找樹更高效，時間複雜度是

O(1)

。既然有了這麼高效的散清單，使用二叉樹的地方是不是都可以替換成散清單呢？有沒有哪些地方是散清單做不了，必須要用二叉樹來做的呢？

二叉查找樹是二叉樹中最常用的一種類型，也叫

二叉搜尋樹

。顧名思義，二叉查找樹是為了實作

快速查找

而生的。不過，它不僅僅支援快速查找一個資料，還支援快速

插入、删除

一個資料。它是怎麼做到這些的呢？

這些都依賴于二叉查找樹的特殊結構。二叉查找樹要求，在樹中的任意一個節點，其

左子樹

中的每個節點的值，都要小于這個節點的值，而

右子樹

節點的值都大于這個節點的值。

• 我們先取根節點，如果它等于我們要查找的資料，那就傳回
• 如果要查找的資料比根節點的值

  小

  ，那就在左子樹中遞歸查找

• 大

  ，那就在右子樹中遞歸查找

public class BinarySearchTree {
  private Node tree;

  public Node find(int data) {
    Node p = tree;
    while (p != null) {
      if (data < p.data) p = p.left;
      else if (data > p.data) p = p.right;
      else return p;
    }
    return null;
  }

  public static class Node {
    private int data;
    private Node left;
    private Node right;

    public Node(int data) {
      this.data = data;
    }
  }
}
           

新插入的資料都是在葉子節點上，是以我們隻需要從根節點開始，依次比較要插入的資料和節點的大小關系。

• 如果要插入的資料比節點的資料

  大

  • 如果節點的右子樹為空，就将新資料直接插到右子節點的位置
  • 如果不為空，就再遞歸周遊右子樹，查找插入位置
• 如果要插入的資料比節點數值

  小

  • 如果節點的左子樹為空，就将新資料插入到左子節點的位置
  • 如果不為空，就再遞歸周遊左子樹，查找插入位置

public void insert(int data) {
  if (tree == null) {
    tree = new Node(data);
    return;
  }

  Node p = tree;
  while (p != null) {
    if (data > p.data) {
      if (p.right == null) {
        p.right = new Node(data);
        return;
      }
      p = p.right;
    } else { //即 data < p.data
      if (p.left == null) {
        p.left = new Node(data);
        return;
      }
      p = p.left;
    }
  }
}
           

二叉查找樹的删除操作相對就比較複雜了，針對要删除節點的

子節點個數

的不同，我們需要分三種情況來處理。

• 如果要删除的節點

  沒有子節點

  ，我們隻需要直接将父節點中，指向要删除節點的指針置為 null。比如圖中的删除節點

  55

• 隻有一個左子節點或者右子節點

  ，我們隻需要更新父節點中，指向要删除節點的指針，讓它指向要删除節點的子節點就可以了。比如圖中的删除節點

  13

• 如果要删除的節點有兩個子節點
  • 我們需要找到這個節點的

    右子樹中的最小節點

    ，把它替換到要删除的節點上
  • 然後再删除掉這個最小節點
  • 因為最小節點肯定沒有左子節點，是以，我們可以應用上面兩條規則來删除這個最小節點。比如圖中的删除節點

    18

public void delete(int data) {
  Node p = tree; // p指向要删除的節點，初始化指向根節點
  Node pp = null; // pp記錄的是p的父節點
  while (p != null && p.data != data) {
    pp = p;
    if (data > p.data) p = p.right;
    else p = p.left;
  }
  if (p == null) return; // 沒有找到

  // 要删除的節點有兩個子節點
  if (p.left != null && p.right != null) { // 查找右子樹中最小節點
    Node minP = p.right;
    Node minPP = p; // minPP表示minP的父節點
    while (minP.left != null) { //最小節點就是最左的子節點，也就是沒有左子節點的結點
      minPP = minP;
      minP = minP.left;
    }
    p.data = minP.data; // 将minP的資料替換到p中
    p = minP; // 下面就變成了删除minP了(即被删除的結點不可能有兩個子節點了)
    pp = minPP;
  }

  // 删除節點是葉子節點或者【僅有一個子節點】
  Node child; // p的子節點
  if (p.left != null) child = p.left; //如果有左子節點，就不會有右子節點
  else if (p.right != null) child = p.right; //如果有又子節點，就不會有左子節點
  else child = null;

  if (pp == null) tree = child; // 删除的是根節點
  else if (pp.left == p) pp.left = child;
  else pp.right = child;
}
           

實際上，關于二叉查找樹的删除操作，還有個非常簡單、取巧的方法，就是單純将要删除的節點

标記

為已删除，但是并不真正從樹中将這個節點去掉。這樣原本删除的節點還需要存儲在記憶體中，比較浪費記憶體空間，但是删除操作就變得簡單了很多。而且，這種處理方法也并沒有增加插入、查找操作代碼實作的難度。

除了插入、删除、查找操作之外，二叉查找樹中還可以支援快速地查找

最大/小節點

、

前驅節點

後繼節點

二叉查找樹除了支援上面幾個操作之外，還有一個重要的特性，就是

中序周遊

二叉查找樹，可以輸出

有序

的資料序列，時間複雜度是

O(n)

，是以，二叉查找樹也叫作

二叉排序樹

有兩種解決方法

• 第一種方法：可以通過

  連結清單

  和支援動态擴容的

  數組

  等資料結構，

  把值相同的資料都存儲在同一個節點上

• 第二種方法：每個節點仍然隻存儲一個資料
  • 在查找

    插入位置

    的過程中，如果碰到一個節點的值與要插入資料的值相同，我們就将這個要插入的資料放到這個節點的

    右子樹

    ，也就是說，把這個新插入的資料當作大于這個節點的值來處理。
  • 查找資料的時候，如果遇到值相同的節點，我們并不停止查找操作，而是

    繼續在右子樹中查找

    ，直到遇到葉子節點才停止。這樣就可以把鍵值等于要查找值的

    所有節點

    都找出來。
  • 對于删除操作，我們也需要先查找到每個要删除的節點，然後再按前面講的删除操作的方法，依次删除。

完全二叉樹的

層數

小于等于

logn + 1

高度

logn

确定二叉樹高度的一種方案：采用

深度優先

的遞歸，分别求左右子樹的高度，目前節點的高度就是左右子樹中較大的那個

+1

在二叉查找樹中，查找、插入、删除等很多操作的時間複雜度都跟樹的

高度

成正比。兩個極端情況的時間複雜度分别是

O(n)

O(logn)

，分别對應二叉樹

退化成連結清單

是完全二叉樹

的情況。

下一節要講的

平衡二叉查找樹

的高度接近

logn

，是以插入、删除、查找操作的時間複雜度也比較穩定，是

O(logn)

相對散清單，二叉查找樹有什麼優勢呢？

第一，散清單中的資料是

無序

存儲的，如果要輸出有序的資料，需要先進行排序。而對于二叉查找樹來說，我們隻需要

中序周遊

，就可以在

O(n)

的時間複雜度内，輸出有序的資料序列。

第二，散清單

擴容

耗時很多，而且當遇到散列沖突時，性能不穩定，盡管二叉查找樹的性能不穩定，但是在工程中，我們最常用的

平衡二叉查找樹

的性能非常穩定，時間複雜度穩定在

O(logn)

第三，籠統地來說，盡管散清單的查找等操作的時間複雜度是常量級的，但因為

哈希沖突

的存在，這個常量不一定比

logn

小，是以實際的查找速度可能不一定比

O(logn)

快。加上

哈希函數的耗時

，也不一定就比平衡二叉查找樹的效率高。

第四，散清單的構造比二叉查找樹要

複雜

，需要考慮的東西很多。比如散列函數的設計、沖突解決辦法、擴容、縮容等。平衡二叉查找樹隻需要考慮

平衡性

這一個問題，而且這個問題的解決方案比較成熟、固定。

最後，為了避免過多的散列沖突，散清單

裝載因子

不能太大，特别是基于開放尋址法解決沖突的散清單，不然會浪費一定的存儲空間。

綜合這幾點，平衡二叉查找樹在某些方面還是優于散清單的，是以，這兩者的存在并不沖突。我們在實際的開發過程中，需要結合具體的需求來選擇使用哪一個。

• 平衡二叉樹

  ：二叉樹中任意一個節點的左右子樹的

  高度相差不能大于 1

• 平衡二叉查找樹

  ：除了滿足上面平衡二叉樹的定義，還滿足二叉查找樹的特點。

最先被發明的平衡二叉查找樹是

AVL

樹，它嚴格符合

平衡二叉查找樹

的定義，即任何節點的左右子樹高度相差不超過 1，是一種高度平衡的二叉查找樹。但是很多平衡二叉查找樹其實并沒有

嚴格符合

上面的定義，比如下面要講的紅黑樹，它從根節點到各個葉子節點的最長路徑，有可能會比最短路徑大一倍。

發明平衡二叉查找樹這類資料結構的初衷是，解決普通二叉查找樹在

頻繁的插入、删除

等動态更新的情況下，出現

時間複雜度退化

的問題。

平衡二叉查找樹中“平衡”的意思，其實就是讓整棵樹左右看起來比較“對稱”、比較“平衡”，不要出現左子樹很高、右子樹很矮的情況。這樣就能讓整棵樹的高度相對來說低一些，相應的插入、删除、查找等操作的效率高一些。

是以，隻要一個平衡二叉查找樹的高度不比

logn

大很多，盡管它不嚴格符合平衡二叉查找樹的定義，但仍然是一個合格的平衡二叉查找樹。

平衡二叉查找樹其實有很多，比如，Splay Tree（伸展樹）、Treap（樹堆）等，但是提到平衡二叉查找樹，聽到的基本都是紅黑樹。它的出鏡率甚至要高于“平衡二叉查找樹”這幾個字，有時候，我們甚至預設平衡二叉查找樹就是紅黑樹。

紅黑樹的英文是

Red-Black Tree

，簡稱

R-B Tree

，它是一種

不嚴格

的平衡二叉查找樹。

紅黑樹中的節點，一類被标記為黑色，一類被标記為紅色。除此之外，一棵紅黑樹還需要滿足這樣幾個要求：

• 根節點是黑色的
• 每個葉子節點都是黑色的空節點（NIL），也就是說，葉子節點不存儲資料
  • 這一條主要是為了簡化紅黑樹的代碼實作而設定的
  • 下面在畫圖和講解的時候，會将黑色的、空的葉子節點都省略掉
• 任何相鄰的節點都不能同時為紅色，也就是說，紅色節點是被黑色節點隔開的
• 每個節點，從該節點到達其可達葉子節點的所有路徑，都包含相同數目的黑色節點

平衡二叉查找樹的初衷是為了解決二叉查找樹因為動态更新導緻的性能退化問題。是以，“平衡”的意思可以等價為性能不退化。“近似平衡”就等價為性能不會退化得太嚴重。

一棵極其平衡的二叉樹（滿二叉樹或完全二叉樹）的高度大約是

logn

，是以如果要證明紅黑樹是近似平衡的，隻需要分析紅黑樹的高度是否比較穩定地趨近

logn

就好了。

後面省略若幹内容......

前面提到的 Treap、Splay Tree，絕大部分情況下，它們操作的效率都很高，但是也

無法避免極端情況下時間複雜度的退化

。盡管這種情況出現的機率不大，但是對于單次操作時間非常敏感的場景來說，它們并不适用。

AVL 樹是一種

高度平衡

的二叉樹，是以查找的效率非常高，但是，有利就有弊，AVL 樹為了維持這種高度的平衡，就要付出更多的代價。每次插入、删除都要做調整，就比較複雜、耗時。是以，對于有頻繁的插入、删除操作的資料集合，使用 AVL 樹的代價就有點高了。

紅黑樹隻是做到了

近似平衡

，并不是嚴格的平衡，是以在維護平衡的成本上，要比 AVL 樹要低。是以，紅黑樹的插入、删除、查找各種操作性能都比較

穩定

，時間複雜度都是

O(logn)

。對于工程應用來說，要面對各種異常情況，為了支撐這種工業級的應用，更傾向于這種

性能穩定

支援動态的資料插入、删除、查找操作的動态資料結構：

• 散清單：插入删除查找都是

  O(1)

  ，是最常用的，但其缺點是不能順序周遊以及擴容縮容的性能損耗。适用于那些不需要順序周遊，資料更新不那麼頻繁的。
• 跳表：插入删除查找都是

  O(logn)

  ，并且能順序周遊。缺點是空間複雜度

  O(n)

  。适用于不那麼在意記憶體空間的，其順序周遊和區間查找非常友善。
• 紅黑樹：插入删除查找都是

  O(logn)

  ，中序周遊即是順序周遊，穩定。缺點是難以實作，去查找不友善。其實跳表更佳，但紅黑樹已經用于很多地方了。

實際上，魔方的複原解法是有固定算法的：遇到哪幾面是什麼樣子，對應就怎麼轉幾下。你隻要跟着這個複原步驟，就肯定能将魔方複原。

紅黑樹的平衡過程跟魔方複原非常神似，大緻過程就是：遇到什麼樣的節點排布，我們就對應怎麼去調整。隻要按照這些固定的調整規則來操作，就能将一個非平衡的紅黑樹調整成平衡的。

• 左旋（rotate left）：圍繞某個節點的左旋
• 右旋（rotate right）：圍繞某個節點的右旋

下圖中的 a，b，r 表示子樹，可以為空

紅黑樹規定，插入的節點必須是紅色的。而且，二叉查找樹中新插入的節點都是放在葉子節點上。是以，關于插入操作的平衡調整，有這樣兩種非常好處理特殊情況：

• 如果插入節點的父節點是

  黑色

  的，那我們什麼都不用做，它仍然滿足紅黑樹的定義
• 如果插入的節點是

  根節點

  ，那我們直接改變它的顔色，把它變成黑色就可以了

除此之外，其他情況都會違背紅黑樹的定義，于是我們就需要進行調整，調整的過程包含兩種基礎的操作：

左右旋轉

改變顔色

紅黑樹的平衡調整過程是一個

疊代

的過程。我們把正在處理的節點叫做

關注節點

。關注節點會随着不停地疊代處理，而不斷發生變化。最開始的關注節點就是新插入的節點。

新節點插入之後，如果紅黑樹的平衡被打破，那一般會有下面三種情況。我們隻需要根據每種情況的特點，不停地調整，就可以讓紅黑樹繼續符合定義，也就是繼續保持平衡。

為了簡化描述，我把父節點的兄弟節點叫做

叔叔節點

，父節點的父節點叫做

祖父節點

CASE 1：如果關注節點是 a，它的叔叔節點 d 是紅色

我們就依次執行下面的操作：

• 将關注節點 a 的父節點 b、叔叔節點 d 的顔色都設定成黑色
• 将關注節點 a 的祖父節點 c 的顔色設定成紅色
• 關注節點變成 a 的祖父節點 c
• 跳到 CASE 2 或者 CASE 3

CASE 2：如果關注節點是 a，它的叔叔節點 d 是黑色，關注節點 a 是其父節點 b 的右子節點

• 關注節點變成節點 a 的父節點 b
• 圍繞新的關注節點 b 左旋
• 跳到 CASE 3

CASE 3：如果關注節點是 a，它的叔叔節點 d 是黑色，關注節點 a 是其父節點 b 的左子節點

• 圍繞關注節點 a 的祖父節點 c 右旋
• 将關注節點 a 的父節點 b、兄弟節點 c 的顔色互換
• 調整結束

紅黑樹插入操作的平衡調整還不是很難，但是它的删除操作的平衡調整相對就要難多了。不過原理都是類似的，我們依舊隻需要根據關注節點與周圍節點的排布特點，按照一定的規則去調整就行了。

删除操作的平衡調整分為兩步，第一步是

針對删除節點初步調整

。初步調整隻是保證整棵紅黑樹在一個節點删除之後，仍然滿足最後一條定義的要求，也就是說，每個節點，從該節點到達其可達葉子節點的所有路徑，都包含相同數目的黑色節點；第二步是

針對關注節點進行二次調整

，讓它滿足紅黑樹的第三條定義，即不存在相鄰的兩個紅色節點。

這裡需要注意一下，紅黑樹的定義中“隻包含紅色節點和黑色節點”，經過初步調整之後，為了保證滿足紅黑樹定義的最後一條要求，有些節點會被标記成兩種顔色，“紅 - 黑”或者“黑 - 黑”。如果一個節點被标記為了“黑 - 黑”，那在計算黑色節點個數的時候，要算成兩個黑色節點。

在下面的講解中，如果一個節點既可以是紅色，也可以是黑色，在畫圖的時候，我會用一半紅色一半黑色來表示。如果一個節點是“紅 - 黑”或者“黑 - 黑”，我會用左上角的一個小黑點來表示額外的黑色。

CASE 1：如果要删除的節點是 a，它隻有一個子節點 b

那我們就依次進行下面的操作：

• 删除節點 a，并且把節點 b 替換到節點 a 的位置，這一部分操作跟普通的二叉查找樹的删除操作一樣
• 節點 a 隻能是黑色，節點 b 也隻能是紅色，其他情況均不符合紅黑樹的定義。這種情況下，我們把節點 b 改為黑色
• 調整結束，不需要進行二次調整

CASE 2：如果要删除的節點 a 有兩個非空子節點，并且它的後繼節點就是節點 a 的右子節點 c

我們就依次進行下面的操作：

• 如果節點 a 的後繼節點就是右子節點 c，那右子節點 c 肯定沒有左子樹。我們把節點 a 删除，并且将節點 c 替換到節點 a 的位置。這一部分操作跟普通的二叉查找樹的删除操作無異
• 然後把節點 c 的顔色設定為跟節點 a 相同的顔色
• 如果節點 c 是黑色，為了不違反紅黑樹的最後一條定義，我們給節點 c 的右子節點 d 多加一個黑色，這個時候節點 d 就成了“紅 - 黑”或者“黑 - 黑”
• 這個時候，關注節點變成了節點 d，第二步的調整操作就會針對關注節點來做

CASE 3：如果要删除的是節點 a，它有兩個非空子節點，并且節點 a 的後繼節點不是右子節點

• 找到後繼節點 d，并将它删除，删除後繼節點 d 的過程參照 CASE 1
• 将節點 a 替換成後繼節點 d
• 把節點 d 的顔色設定為跟節點 a 相同的顔色
• 如果節點 d 是黑色，為了不違反紅黑樹的最後一條定義，我們給節點 d 的右子節點 c 多加一個黑色，這個時候節點 c 就成了“紅 - 黑”或者“黑 - 黑”
• 這個時候，關注節點變成了節點 c，第二步的調整操作就會針對關注節點來做

經過初步調整之後，關注節點變成了“紅 - 黑”或者“黑 - 黑”節點。針對這個關注節點，我們再分四種情況來進行二次調整。二次調整是為了讓紅黑樹中不存在相鄰的紅色節點。

CASE 1：如果關注節點是 a，它的兄弟節點 c 是紅色的

• 圍繞關注節點 a 的父節點 b 左旋
• 關注節點 a 的父節點 b 和祖父節點 c 交換顔色
• 關注節點不變
• 繼續從四種情況中選擇适合的規則來調整

CASE 2：如果關注節點是 a，它的兄弟節點 c 是黑色的，并且節點 c 的左右子節點 d、e 都是黑色的

• 将關注節點 a 的兄弟節點 c 的顔色變成紅色
• 從關注節點 a 中去掉一個黑色，這個時候節點 a 就是單純的紅色或者黑色
• 給關注節點 a 的父節點 b 添加一個黑色，這個時候節點 b 就變成了“紅 - 黑”或者“黑 - 黑”
• 關注節點從 a 變成其父節點 b
• 繼續從四種情況中選擇符合的規則來調整

CASE 3：如果關注節點是 a，它的兄弟節點 c 是黑色，c 的左子節點 d 是紅色，c 的右子節點 e 是黑色

• 圍繞關注節點 a 的兄弟節點 c 右旋
• 節點 c 和節點 d 交換顔色
• 跳轉到 CASE 4，繼續調整

CASE 4：如果關注節點 a 的兄弟節點 c 是黑色的，并且 c 的右子節點是紅色的

• 将關注節點 a 的兄弟節點 c 的顔色，跟關注節點 a 的父節點 b 設定成相同的顔色
• 将關注節點 a 的父節點 b 的顔色設定為黑色
• 從關注節點 a 中去掉一個黑色，節點 a 就變成了單純的紅色或者黑色
• 将關注節點 a 的叔叔節點 e 設定為黑色

為什麼紅黑樹的定義中，要求葉子節點是黑色的空節點？

之是以有這麼奇怪的要求，其實就是為了實作起來友善。隻要滿足這一條要求，那在任何時刻，紅黑樹的平衡操作都可以歸結為我們剛剛講的那幾種情況。

假設紅黑樹的定義中不包含剛剛提到的那一條“葉子節點必須是黑色的空節點”，我們往一棵紅黑樹中插入一個資料，新插入節點的父節點也是紅色的，兩個紅色的節點相鄰，這個時候，紅黑樹的定義就被破壞了。那我們應該如何調整呢？

你會發現，這個時候，我們前面在講插入時，三種情況下的平衡調整規則，沒有一種是适用的。但是，如果我們把黑色的空節點都給它加上，變成下面這樣，你會發現，它滿足 CASE 2 了。

你可能會說，你可以調整一下平衡調整規則啊。比如把 CASE 2 改為“如果關注節點 a 的叔叔節點 b 是黑色或者不存在，a 是父節點的右子節點，就進行某某操作”。當然可以，但是這樣的話規則就沒有原來簡潔了。

你可能還會說，這樣給紅黑樹添加黑色的空的葉子節點，會不會比較浪費存儲空間呢？答案是不會的。雖然我們在講解或者畫圖的時候，每個黑色的、空的葉子節點都是獨立畫出來的。實際上，在具體實作的時候，我們隻需要像下面這樣，共用一個黑色的、空的葉子節點就行了。

很多人都認為紅黑樹很難學，其實主要原因是，他們都試圖去記住它的

平衡調整政策

。實際上，你隻需要

了解

這個調整過程就可以了，沒有必要去記。

現在，我就來總結一下，如何比較輕松地看懂我今天講的操作過程。

• 第一點，把紅黑樹的平衡調整的過程比作

  魔方複原

  ，不要過于深究這個算法的正确性。你隻需要明白，隻要

  按照固定的操作步驟

  ，保持插入、删除的過程，不破壞平衡樹的定義就行了。
• 第二點，找準

  關注節點

  ，不要搞丢、搞錯關注節點。因為每種操作規則，都是基于關注節點來做的，隻有弄對了關注節點，才能對應到正确的操作規則中。在疊代的調整過程中，關注節點在不停地改變，是以，這個過程一定要注意，不要弄丢了關注節點。
• 第三點，插入操作的平衡調整比較簡單，但是删除操作就比較複雜。針對删除操作，我們有兩次調整，第一次是針對要删除的節點做初步調整，讓調整後的紅黑樹繼續滿足第四條定義。但是這個時候，第三條定義就不滿足了，有可能會存在兩個紅色節點相鄰的情況。第二次調整就是解決這個問題，讓紅黑樹不存在相鄰的紅色節點。

遞歸代碼的

時間複雜度

分析起來很麻煩，前面我們講過如何利用

遞推公式

求解歸并排序、快速排序的時間複雜度。但是，有些情況用遞推公式的話，會涉及非常複雜的數學推導。今天，我們就來學習另外一種方法，借助

遞歸樹

來分析遞歸算法的時間複雜度。

遞歸的思想就是将大問題分解為小問題來求解，然後再将小問題分解為小小問題。這樣一層一層地分解，直到問題的資料規模被分解得足夠小，不用繼續遞歸分解為止。

如果我們把這個一層一層的

分解過程

畫成圖，它其實就是一棵樹。我們給這棵樹起一個名字，叫作

遞歸樹

下圖是

斐波那契數列

的遞歸樹，節點裡的數字表示資料的規模，一個節點的求解可以分解為左右子節點兩個問題的求解。

利用遞歸樹的時間複雜度分析方法并不難了解，關鍵還是在實戰。

歸并排序每次會将資料規模一分為二，現在我們就借助歸并排序來看看如何用遞歸樹，分析遞歸代碼的時間複雜度。

我們把歸并排序畫成遞歸樹，就是下面這個樣子：

歸并算法中比較耗時的是

歸并操作

，也就是把兩個

子數組

合并為

大數組

。從圖中我們可以看出，

每一層歸并操作消耗的時間總和是一樣的

，跟要排序的資料規模有關，我們把每一層歸并操作消耗的時間記作 n。

現在，我們隻需要知道這棵樹的高度 h，用高度 h 乘以每一層的時間消耗 n，就可以得到總的時間複雜度

O(n∗h)

從歸并排序的原理和遞歸樹可以看出來，歸并排序遞歸樹是一棵

滿二叉樹

，滿二叉樹的高度大約是

logn

，是以，歸并排序遞歸實作的時間複雜度就是

O(nlogn)

為什麼用遞推公式來求解平均時間複雜度非常複雜？

快速排序在最好情況下，每次分區都能一分為二，這個時候用遞推公式

T(n) = 2*T(n/2) + n

，很容易就能推導出時間複雜度是

O(nlogn)

。但是，我們并不可能每次分區都正好一分為二。

假設平均情況下，每次分區之後，兩個分區的大小比例為

1:k

。當 k=9 時，用遞推公式的方法來求解時間複雜度的話，遞推公式就寫成

T(n)=T(n/10) + T(9n/10) + n

這個公式可以推導出時間複雜度，但是推導過程非常複雜。

如果我們把遞歸分解的過程畫成遞歸樹，就是下面這個樣子：

快速排序的過程中，每次分區都要周遊待分區區間的所有資料，是以，

每一層

分區操作所周遊的資料的個數之和就是 n。我們現在隻要求出遞歸樹的高度 h，這個快排過程周遊的資料個數就是

h∗n

，也就是說，時間複雜度就是

O(h∗n)

因為每次分區并不是均勻地一分為二，是以遞歸樹并不是滿二叉樹。這樣一個遞歸樹的高度是多少呢？

我們知道，快速排序結束的條件就是待排序的小區間大小為 1，也就是說葉子節點裡的資料規模是 1。從根節點 n 到葉子節點 1，遞歸樹中最短的一個路徑每次都乘以

1/10

，最長的一個路徑每次都乘以

9/10

。通過計算，我們可以得到：

是以，周遊資料的個數總和就介于最短路徑和最長路徑之間，是以，當分區大小比例是

1:9

時，快速排序的時間複雜度仍然是

O(nlogn)

剛剛我們假設 k=9，那如果 k=99，也就是說，每次分區極其不平均，兩個區間大小是

1:99

，這個時候的時間複雜度是多少呢？

我們可以類比上面 k=9 的分析過程。當 k=99 的時候，盡管底數變了，但是時間複雜度也仍然是

O(nlogn)

也就是說，對于 k 等于 9，99，甚至是 999，9999……，隻要

k 的值不随 n 變化

，是一個事先确定的常量，那快排的時間複雜度就是

O(nlogn)

斐波那契數列的代碼實作

int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  return f(n-1) + f(n-2);
}
           

把上面的遞歸代碼畫成遞歸樹，就是下面這個樣子：

這棵遞歸樹的高度是多少呢？

f(n) 分解為

f(n−1)

f(n−2)

，每次資料規模都是 −1 或者 −2，是以，從根節點走到葉子節點，每條路徑是長短不一的。如果每次都是 −1，那最長路徑大約就是

n

；如果每次都是 −2，那最短路徑大約就是

n/2

每次分解之後的合并操作隻需要一次加法運算，我們把這次加法運算的時間消耗記作 1。是以，從上往下，第一層的總時間消耗是 1，第二層的總時間消耗是 2，第三層的總時間消耗就是

2^2

。依次類推，第 k 層的時間消耗就是

2^(k−1)

，那整個算法的總的時間消耗就是每一層時間消耗之和。

如果路徑長度都為 n，那這個總和就是

2^n − 1

是以，這個算法的時間複雜度就介于

O(2^n)

O(2^n/2)

之間。

如何把 n 個資料的所有排列都找出來，這就是全排列的問題。

比如，1，2，3 這樣 3 個資料，有下面這幾種不同的排列：

1, 2, 3
1, 3, 2
2, 1, 3
2, 3, 1
3, 1, 2
3, 2, 1
           

如何程式設計列印一組資料的所有排列呢？這裡就可以用遞歸來實作。

如果我們确定了最後一位資料，那就變成了求解剩下

n−1

個資料的排列問題。而最後一位資料可以是 n 個資料中的任意一個，是以它的取值就有 n 種情況。是以，n 個資料的全排列問題，就可以分解成 n 個

n−1

個資料的全排列的子問題。

遞推公式：

假設數組中存儲的是1，2， 3...n
f(1,2,...n) = {最後一位是1, f(n-1)} + {最後一位是2, f(n-1)} + ... + {最後一位是n, f(n-1)}
           

// 調用方式：
// int[]a = a={1, 2, 3, 4}; printPermutations(a, 4, 4);
// k表示要處理的子數組的資料個數
public void printPermutations(int[] data, int n, int k) {
  if (k == 1) {
    for (int i = 0; i < n; ++i) {
      System.out.print(data[i] + " ");
    }
    System.out.println();
  }

  for (int i = 0; i < k; ++i) {
    int tmp = data[i];
    data[i] = data[k-1];
    data[k-1] = tmp;

    printPermutations(data, n, k - 1);

    tmp = data[i];
    data[i] = data[k-1];
    data[k-1] = tmp;
  }
}

           

如果不用遞歸樹分析方法，這個遞歸代碼的時間複雜度會比較難分析。

首先，我們還是畫出遞歸樹。不過，現在的遞歸樹已經不是标準的二叉樹了。

第一層分解有 n 次交換操作，第二層有 n 個節點，每個節點分解需要

n−1

次交換，是以第二層總的交換次數是

n∗(n−1)

。第三層有

n∗(n−1)

個節點，每個節點分解需要

n−2

次交換，是以第三層總的交換次數是

n∗(n−1)∗(n−2)

以此類推，第 k 層總的交換次數就是

n∗(n−1)∗(n−2)∗...∗(n−k+1)

。最後一層的交換次數就是

n∗(n−1)∗(n−2)∗...∗2∗1

。每一層的交換次數之和就是總的交換次數。

n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1
           

這個公式的求和比較複雜，我們看最後一個數，

n∗(n−1)∗(n−2)∗...∗2∗1

等于

n!

，而前面的 n−1 個數都小于最後一個數，是以，總和肯定小于

n∗n!

，也就是說，全排列的遞歸算法的時間複雜度大于

O(n!)

，小于

O(n∗n!)

，雖然我們沒法知道非常精确的時間複雜度，但是這樣一個範圍已經讓我們知道，全排列的時間複雜度是非常高的。

掌握分析的方法很重要，思路是重點，不要糾結于精确的時間複雜度到底是多少。

• 有些代碼的時間複雜度比較适合用

  遞推公式

  來分析，比如歸并排序、快速排序的最好情況時間複雜度
• 有些比較适合采用

  遞歸樹

  來分析，比如快速排序的平均時間複雜度
• 有些可能兩個都不怎麼适合使用，比如二叉樹的遞歸前中後序周遊

2021-9-1

本文來自部落格園，作者：白乾濤，轉載請注明原文連結：https://www.cnblogs.com/baiqiantao/p/15216490.html