前言
Cassandra是一款NoSQL分布式資料庫,采用LSM Tree架構。衆所周知,LSM有兩個重要過程:資料順序刷入磁盤生成資料檔案(SSTable)和 資料檔案合并(Compaction)。今天本文主要說一個Compaction過程中的優化。
資料檔案合并(Compaction)
首先我們要明白Compaction這個過程到底要做什麼事,再來看如何優化。我們先從資料檔案(SSTable)說起。
SSTable: Sorted String Table
這個詞源自Google BigTable論文,是一個不可修改的資料檔案。最初資料來自于使用者寫入,并且緩存在記憶體中。當緩存滿的時候,會将緩存中的資料刷入磁盤,也就生成了SSTable檔案。刷入磁盤的SSTable裡的資料是排好序的。比如,使用者寫入
[1, 0, 2, 4]
這麼4條資料,最後刷入磁盤,這4條資料在SSTable裡的排列是這樣的
[0, 1, 2, 4]
。
通過寫緩存,可以利用磁盤順序寫性能更好的特點,尤其是機械盤。查詢過程也很簡單,因為資料排好序,隻要二分搜尋即可。
為什麼要做Compaction
随着資料不斷寫入,緩存不斷刷入磁盤生成SSTable的時候,我們會擁有很多SSTable。這時候會有什麼問題呢?可以試想一下下面這個場景:
- 使用者先寫入
[1, 3, 8, 2]
[1, 2, 3, 8]
- 使用者再寫入
[0, 3, 7, 6]
[0, 3, 6, 7]
這時候如果要查詢
3
,不得不通路2個檔案。因為2個檔案都包含了
3
,得确定哪個
3
是最新的。更惡心的情況是,使用者繼續寫入
[0, 4, 5, 9]
,雖然沒有
3
,但是因為這個
0~9
這個範圍包含了
3
,你任然需要搜尋這個檔案,确定有沒有你要的資料(這種落空的情況可以通過Bloom filter優化)。
如果SSTable檔案很多,查詢效率就會顯著下降。那麼解決這個問題,就是做Compaction。将SSTable0和SSTable1合并後,我們能得到
[0, 1, 2, 3, 6, 7, 8]
,一個全新的SSTable,後續查詢隻要搜尋這個新的SSTable檔案即可。
這就是Compaction主要的作用,當然Compaction過程中還有一個重要任務是清理過期或者被删除的資料。
簡單抽象一下Compaction過程:多個有序連結清單去重合并
如何合并多個有序連結清單
相信很多同學面試也遇到過這個問題,很直接的想法就是用一個優先隊列解決。Java中是
PriorityQueue
這個類,它的實作就是一個小根堆。代碼也很好實作:
public List<Integer> doCompaction(Iterator<Integer>[] sstables) {
LinkedList<Integer> result = new LinkedList<>();
Integer[] topElement = new Integer[sstables.length];
PriorityQueue<Integer> heap = new PriorityQueue<>(
(idx1, idx2) -> topElement[idx1] - topElement[idx2]
);
// 初始化
for (int i = 0; i < sstables.length; i++) {
if (sstables[i].hasNext()) {
topElement[i] = sstables[i].next();
heap.add(i);
}
}
while (!heap.isEmpty()) {
int sstableIdx = heap.poll(); // 最小元素出隊
// 去重
if (result.isEmpty() || result.getLast() < topElement[sstableIdx]) {
result.add(topElement[sstableIdx]);
} else {
assert result.getLast() == topElement[sstableIdx];
}
if (sstables[sstableIdx].hasNext()) {
topElement[sstableIdx] = sstables[sstableIdx].next();
heap.add(sstableIdx); // 新元素入隊
}
}
return result;
} 這個複雜度是
O(N·logM)
, N是總共的元素個數,M是有序連結清單數量。這個實作方法要比直接連一起排序快,直接排序是
O(N·logN)
。顯然
N>=M
,是以前者更快。
優化1
上述方法看起來沒有什麼大問題,Cassandra之前一些版本也是這麼實作的。但是仔細分析這個過程,會發現有一些不必要的開銷。
首先每個元素都會經曆
poll
和
add
兩個過程,這兩個過程的開銷都是
O(logM)
。作為一個通用的PriorityQueue,poll和add之後都要保持堆的結構特性,所有要做下濾(shift down)和上濾(shift up),這兩個操作都是
O(logM)
。poll之後,因為堆頂缺失,會将最後一個元素放到堆頂做一次下濾。add元素則直接放到堆尾,做一次上濾。
是以精确一點複雜度是
O(2N·logM)
。但是因為我們基本每次poll元素後都會再add一個元素,那麼可以直接将新add的元素放入堆頂做一次下濾。這樣就将原來 一次下濾&一次上濾 合成 一次下濾。這樣理論上直接節省一半時間。
優化前過程:
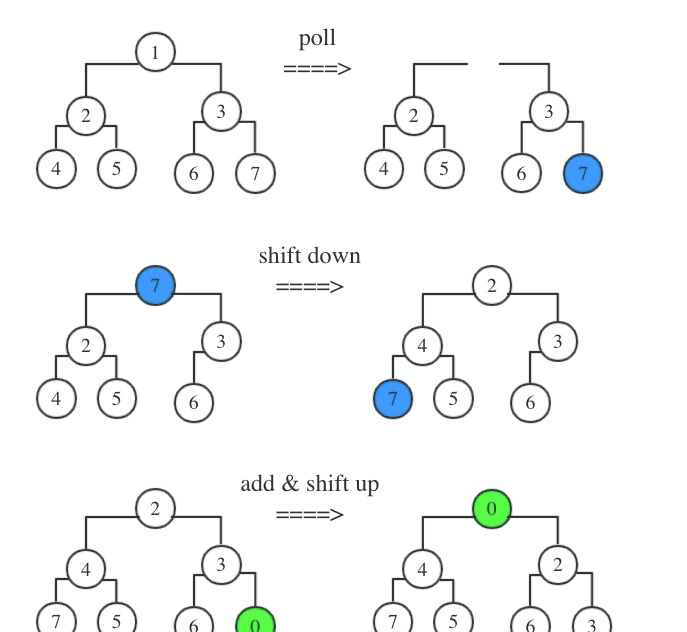
優化後過程:
這個在SSTable資料基本不怎麼重疊的情況下,效果更好。因為某個SSTable彈出的資料可能會一直處于堆頂,下濾隻需要比較2次即可。
優化2
下濾調整元素的時候,每一層,需要做2次比較。先比較2個子節點誰最小,再把父節點和最小的比。
如果考慮上面說的那種情況,重疊比較少,某個SSTable一段連續的資料可能會一直最小,會處于堆頂,那麼一直隻需要2次比較就能确定堆頂元素。如果堆頂不是一個二叉,而是一個單鍊,那就隻需要1次比較即可。是以Cassandra裡的堆,是一個很短的有序單鍊 + 一個堆。這種情況還是挺常見的,經過一段時間的壓縮後,尤其對于使用
LeveledCompactionStrategy
的場景來說。
最終堆形狀如下:
優化3
引入一個
equalParent
變量,表示該元素是否和父節點相等。這樣可以進一步節約一些比較次數,在某些情況下。比較是位元組數組比較,是以還是有一定開銷的,并不像文中抽象的問題那樣,簡單比較整數。
寫在最後
為了營造一個開放的Cassandra技術交流環境,社群建立了微信公衆号和釘釘群。為廣大使用者提供專業的技術分享及問答,定期開展專家技術直播,歡迎大家加入。另阿裡雲為廣大開發者提供雲上Cassandra資源,可用于動手實踐:9.9元可使用三月(限首購)。
直達連結:
https://www.aliyun.com/product/cds