算法題之動态規劃-01背包問題

文章首發于我的個人部落格，到個人部落格體驗更佳閱讀哦

https://www.itqiankun.com/article/1564909352

文字介紹解決背包問題

假設山洞裡共有a,b,c,d ,e這5件寶物（不是5種寶物），它們的重量分别是2,2,6,5,4，它們的價值分别是6,3,5,4,6，現在給你個承重為10的背包, 怎麼裝背包，可以才能帶走最多的财富。

此時隻要了解了狀态轉換方程f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }，就知道這道算法的答案了，這個狀态轉換方程是怎麼來的呢？往下看

假如背包要放第i件物品，此時如果不放第i件物品，那麼問題就轉化為“前i-1件物品放入重量是w的背包中”，價值為f[i-1,j]；
如果放第i件物品，那麼問題就轉化為“前i-1件物品放入剩下的重量為j-Wi的背包中”，此時能獲得的最大價值就是f[i-1,j-Wi]
再加上通過放入第i件物品獲得的價值Pi，此時隻要比較f[i-1,j]和f[i-1,j-Wi]+Pi那個大就能擷取到背包裡最大的價值是多少了。           

可能還是不是太懂，那麼我們看圖來了解，這裡就使用大佬的圖檔了，就是下面的圖檔，有編号分别為a,b,c,d,e的五件物品，它們的重量分别是2,2,6,5,4，它們的價值分别是6,3,5,4,6，現在給你個承重為10的背包，怎麼擷取價值最大的背包呢

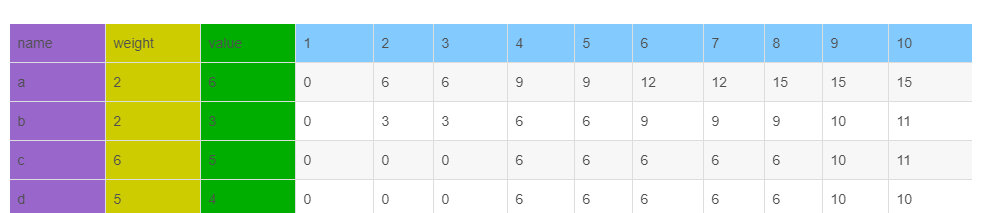
首先對這個圖檔要知道的是：

• 明确這張表是至底向上，從左到右生成的。

• 然後用e2單元格表示e行2列的單元格，這個單元格的意義是用來表示隻有物品e時，有個承重為2的背包，那麼這個背包的最大價值是0，因為e物品的重量是4，背包裝不了。
• 對于d2單元格，表示隻有物品e，d時,承重為2的背包,所能裝入的最大價值，仍然是0，因為物品e,d都不是這個背包能裝的。
• 同理，c2=0，b2=3,a2=6。

對于承重為8的背包，a8=15,是怎麼得出的呢？根據01背包的狀态轉換方程，需要考察兩個值，就是下面的兩個

• 一個是f[i-1,j]，這種情況就是承重為8的背包裡面不放a這個物品這一種情況(根據上面的狀态轉換方程來的)，這裡i就是下面的橫列的值，然後j就是指豎列的值，是以此時f[i-1,j]裡面的i就是a、j就是8，因為a的下一列是b，是以f[i-1,j]就是指b8，是以此時的f[i-1,j]的值就是9
• 另一個是f[i-1,j-Wi]+Pi，這種情況就是承重為8的背包裡面要放a這個物品這一種情況(根據上面的狀态轉換方程來的)，既然要放a這個物品，那麼此時的Pi的值就是6(因為a商品的價值是6)，然後因為承重為8的背包裡面已經确定要放a這個物品，是以此時這個背包裡面最多還隻能存放的重量就是6，這裡i就是下面的橫列的值，然後j就是指豎列的值，是以此時f[i-1,j-Wi]裡面的i就是a、j就是8、Wi就是2(這個2就是a物品的重量)，是以此時f[i-1,j-Wi]就是指b6，此時b6的值是9，是以f[i-1,j-Wi]+Pi=9+6=15，是以物品a應該放入稱重是8的背包裡面

java代碼解答這個背包問題

下面的紅色代碼注釋裡面的數組裡面的第一個索引都是0，這是為了避免數組的0索引問題

下面的藍色代碼注釋裡面的for循環目的就是為了建立 這樣的一個圖檔

，然後隻要建立好上面的圖檔，那麼我們就能知道背包問題的答案了

package com.one.util;

public class Test {
    public static int getMaxValue(int[] weight, int[] value, int w, int n) {
        int[][] table = new int[n + 1][w + 1];// 建立一個二維數組，橫列是物品的價值，豎列是物品的重量
        // 藍色代碼注釋開始
        for (int i = 1; i <= n; i++) { //物品
            for (int j = 1; j <= w; j++) {  //背包大小
                if (weight[i] > j) {
                    //目前物品i的重量比背包容量j大，裝不下，肯定就是不裝
                    table[i][j] = table[i - 1][j];
                } else { //裝得下，Max{裝物品i， 不裝物品i}
                    table[i][j] = Math.max(table[i - 1][j], table[i - 1][j - weight[i]] + value[i]);
                }
            }
        }
        // 藍色代碼注釋結束
        return table[n][w];
    }

    public static void main(String[] args) {
        int n = 5, w = 10;                    //物品個數，背包容量
        // 紅色代碼注釋開始
        int[] value = {0,6, 3, 5, 4, 6};     //各個物品的價值
        int[] weight = {0,2, 2, 6, 5, 4};    //各個物品的重量
        // 紅色代碼注釋結束
        System.out.println(getMaxValue(weight, value, w, n));
    }
}           

原文連結

大佬連結