LeetCode 118：楊輝三角 II Pascal's Triangle II

公衆号：愛寫bug（ID：icodebugs）

作者：愛寫bug

給定一個非負索引 k，其中 k ≤ 33，傳回楊輝三角的第 k 行。

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal's triangle.

Note that the row index starts from 0.

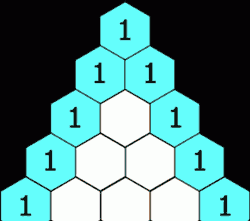
在楊輝三角中，每個數是它左上方和右上方的數的和。

In Pascal's triangle, each number is the sum of the two numbers directly above it.

示例:

輸入: 3
輸出: [1,3,3,1]           

進階：

你可以優化你的算法到 O(k) 空間複雜度嗎？

解題思路：

和之前寫的那篇118号楊輝三角基本類似。這道題隻是不用考慮每行輸出，隻輸出最後一行。這樣隻在一個數組上修改即可：該數 的值 = 該數的值+該數左邊的值之和（該數不包括第一個和最後一個數）。

這道題隻是不用考慮每一行輸出，隻輸出最後一行。這樣隻在一個數組上修改即可：該數 的值 = 該數的值+該數左邊的值之和（該數不包括第一個和最後一個數）。

用兩個嵌套循環，外循環是要計算的每行數組，内循環在上一次計算的數組基礎上更改數值得出該行數組。

需要注意的是：内循環 j 指針應該從每行的最後一個數開始更改。

如果 j 指針從左開始更改索引的值：

[1]

[1,1]

[1,2,1] 索引1 的值是索引 0 和 1的和，沒問題

[1,3,4,1] 索引2 的值是索引 2 和索引 1的和 為4，而不是預期的3

因為我們是在同一個數組裡更改每個數值的，是以如果做左邊開始求值，索引 1 的值會從2變為3，此時計算索引2的值，由于該索引左邊的值已經改變為3，該索引将不再是預期值。

起先我用的是

ArrayList<Integer>()

：

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> nums = new ArrayList<Integer>();
        nums.add(1);
        for (int i = 1; i <= rowIndex; i++) {
            for (int j = i - 1; j > 0; j--) {
                nums.set(j, nums.get(j) + nums.get(j - 1));
            }
            nums.add(1);
            System.out.println(nums);
        }
        return nums;
    }
}           

送出時雖然能通過但是每次調用 set()、add() 導緻性能很差很差。

Java：

class Solution {
    public List<Integer> getRow(int rowIndex) {
        Integer[] nums = new Integer[rowIndex+1];//所有值被預設置為0
        Arrays.fill(nums, 0);
        nums[0] = 1;
        for (int i = 1; i <= rowIndex; i++) {
            for (int j = i; j >0; j--) {
                nums[j] = nums[j] + nums[j-1];//當j為1時，nums[j]為0，不影響最後一個值，不用單獨給每行末尾指派1
            }
        }
        return Arrays.asList(nums);//轉為List<Integer>型并傳回
    }
}           

Python3：

class Solution:
    def getRow(self, rowIndex: int) -> List[int]:
        nums = [1] 
        for i in range(1, rowIndex+1):
            for j in range(i-1, 0, -1):
                nums[j] +=nums[j-1]
            nums.append(1) # 需要給末尾索引指派1
        return nums