資料科學家Jeremy Howard在fast.ai的《生成對抗網絡(GAN)》課程中曾經講過這樣一句話:
“從本質上來說,生成對抗網絡(GAN)是一種特殊的損失函數。”
你是否能夠了解這句話的意思?讀完本文,你會更好的了解這句話的含義。
神經網絡的函數逼近理論在數學中,我們可以将函數看做一個“機器”或“黑匣子”,我們為這個“機器”或“黑匣子”提供了一個或多個數字作為輸入,則會輸出一個或多個數字,如下圖所示:
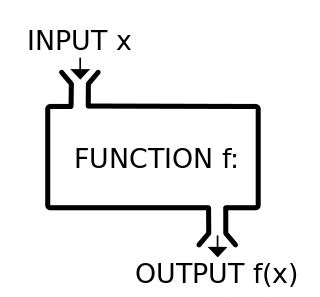
将函數可以比喻成一個“機器”或“黑匣子”
一般來說,我們可以用一個數學表達式來表示我們想要的函數。但是,在一些特殊的情況下,我們就沒辦法将函數寫成一堆加法和乘法的明确組合,比如:我們希望擁有這樣一個函數,即能夠判斷輸入圖像的類别是貓還是狗。
如果不能用明确的用數學表達式來表達這個函數,那麼,我們可以用某種方法近似表示嗎?
這個近似方法就是神經網絡。
通用近似定理表明,如果一個前饋神經網絡具有線性輸出層和至少一層隐藏層,隻要給予網絡足夠數量的神經元,便可以表示任何一個函數。
具有4個隐藏單元的簡單神經網絡逼近函數
作為損失函數的神經網絡現在,我們希望設計一個貓和狗的分類器。但我們沒辦法設計一個特别明确的分類函數,是以我們另辟蹊徑,建構一個神經網絡,然後一步一步逐漸實作這一目标。
為了更好的逼近,神經網絡需要知道距離目标到底還有多遠。我們使用損失函數表示誤差。
現在,存在很多種類型的損失函數,使用哪種損失函數則取決于手頭上的任務。并且,他們有一個共同的屬性,即這些損失函數必須能夠用精确的數學表達式來表示,如:
1.L1損失函數(絕對誤差):用于回歸任務。
2.L2損失函數(均方誤差):和L1損失函數類似,但對異常值更加敏感。
3.交叉熵損失函數:通常用于分類任務。
4.Dice系數損失函數:用于分割任務。
5.相對熵:又稱KL散度,用于測量兩個分布之間的差異。
在建構一個性能良好的神經網絡時,損失函數非常有用。正确深入的了解損失函數,并适時使用損失函數實作目标,是開發人員必備的技能之一。
如何設計一個好的損失函數,也是一個異常活躍的研究領域。比如:《密度對象檢測的焦點損失函數(Focal Loss)》中就設計了一種新的損失函數,稱為焦點損失函數,可以處理人臉檢測模型中的差異。
可明确表示損失函數的一些限制上文提到的損失函數适用于分類、回歸、分割等任務,但是如果模型的輸出具有多模态分布,這些損失函數就派不上用場了。比如,對黑白圖像進行着色處理。
如上圖所示:
1.輸入圖像是個黑白鳥類圖像,真實圖像的顔色是藍色。
2.使用L2損失函數計算模型輸出的彩色圖像和藍色真實圖像之間的差異。
3.接下來,我們有一張非常類似的黑白鳥類圖像,其真實圖像的顔色是紅色。
4.L2損失函數現在嘗試着将模型輸出的顔色和紅色的差異最小化。
5.根據L2損失函數的回報,模型學習到:對于類似的鳥類,其輸出可以接近紅色,也可以接近藍色,那麼,到底應該怎麼做呢?
6.最後,模型輸出鳥類的顔色為黃色,這就是處于紅色和藍色中間的顔色,并且是差異最小化的安全選擇,即便是模型以前從未見過黃色的鳥,它也會這樣做。
7.但是,自然界中沒有黃色的鳥類,是以模型的輸出并不真實。
使用MSE預測的下一幀圖像非常模糊
在很多情況下,這種平均效果并不理想。舉個例子來說,如果需要模型預測視訊中下一個幀圖像,下一個幀有很多種可能,你肯定希望模型輸出其中一種可能,然如果使用L1或L2損失函數,模型會将所有可能性平均化,輸出一個特别模型的平均圖像,這就和我們的目标相悖。
生成對抗網絡 —— 一種新的損失函數如果我們沒辦法用明确的數學表達式來表示這個損失函數,那麼,我們就可以使用神經網絡進行逼近,比如,函數接收一組數字,并輸出狗的真實圖像。
神經網絡需要使用損失函數來回報目前結果如何,但是并沒有哪個損失函數可以很好的實作這一目标。
會不會有這樣一種方法?能夠直接逼近神經網絡的損失函數,但是我們沒必要知道其數學表達式是什麼,這就像一個“機器”或“黑匣子”,就跟神經網絡一樣。也就是說,如果使用一個神經網絡模型替換這個損失函數,這樣可以嗎?
對,這就是生成對抗網絡(GAN)。
Vanilla-GAN架構
Alpha-GAN架構
我們來看上面兩個圖,就可以更好的了解損失函數。在上圖中,白色框表示輸入,粉色和綠色框表示我們要建構的神經網絡,藍色表示損失函數。
在vanilla
GAN中,隻有一個損失函數,即判别器D,這本身就是一個特殊的神經網絡。
而在Alpha-GAN中,有3個損失函數,即輸入資料的判别器D,編碼潛在變量的潛在判别器C和傳統的像素級L1損失函數。其中,D和C不是明确的損失函數,而是一種逼近,即一個神經網絡。
梯度如果使用損失函數訓練生成網絡(和Alpha-GAN網絡中的編碼器),那麼,應該使用哪種損失函數來訓練判别器呢?
判别器的任務是區分實際資料分布和生成資料分布,使用監督的方式訓練判别器比較容易,如二進制交叉熵。由于判别器是生成器的損失韓式,這就意味着,判别器的二進制交叉熵損失函數産生的梯度也可以用來更新生成器。
結論考慮到神經網絡可以代替傳統的損失函數,生成對抗網絡就實作了這一目标。兩個網絡之間的互相作用,可以讓神經網絡執行一些以前無法實作的任務,比如生成逼真的圖像等任務。
本文由北郵
@愛可可-愛生活老師推薦,
阿裡雲雲栖社群組織翻譯。
文章原标題《GANs as a loss function》
譯者:Mags,審校:袁虎。
文章為簡譯,更為詳細的内容,請檢視
原文