動态規劃問題-爬樓梯

動态規劃的核心：我目前也說不清楚，知道動态規劃可以解決很多問題。

爬樓梯：

假設你正在爬樓梯。需要 n 步你才能到達樓頂。

每次你可以爬 1 或 2 個台階。你有多少種不同的方法可以爬到樓頂呢？

注意：給定 n 是一個正整數。

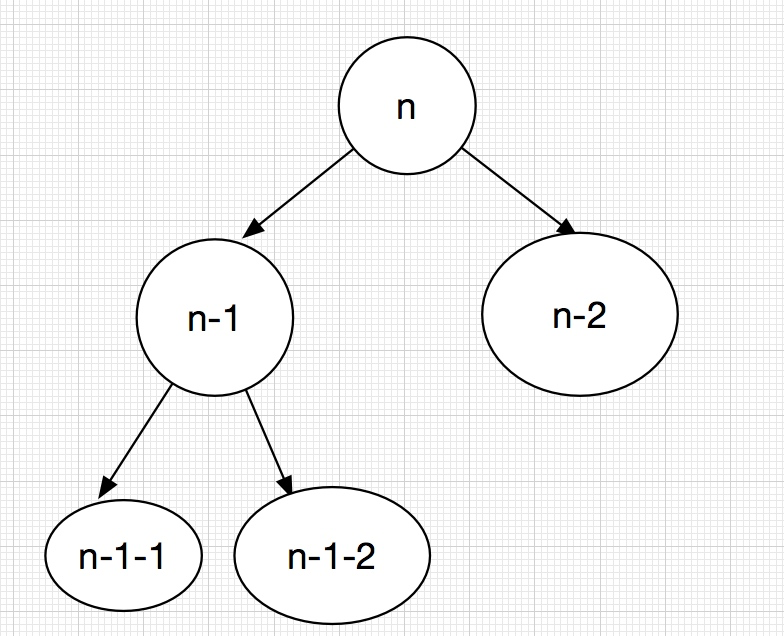
image.png

分析：

1. 假設目前我們在n層樓梯，下面可以走一層或兩層 變成n-1或n-2
2. n-1層和n-2層又可以回到第一步繼續走

代碼

分别運用了遞歸與非遞歸的方法。

注釋掉的代碼為非遞歸方法，未注釋掉的為遞歸方法。

class Solution {
    public int climbStairs(int n) {
        // if (n == 0 || n == 1 || n == 2) {
        //  return n;
        // }
        // int[] r = new int[n+1];
        // r[1] = 1;
        // r[2] = 2;
        // for (int i = 3; i <= n; i++) {
        // r[i] = r[i-1] + r[i-2];
        // }
        // return r[n];  
        int[] arr = new int[n];
        return doClimb(n,arr);
    }
    
    int doClimb(int n,int[] arr){
        if(n == 0){
            return 0;
        }
        if(n == 1){
            return 1;
        }
        if(n == 2){
            return 2;
        }
        if(arr[n-1] != 0){
            return arr[n-1];
        }else{
            arr[n-1] = doClimb(n-1,arr) + doClimb(n-2,arr);
        }
        return arr[n-1];
            
    }
}

           

最後

動态規劃問題，多練習才能熟能生巧。