目錄:
● 神經網絡前言
● 神經網絡
● 感覺機模型
● 多層神經網絡
● 激活函數
● Logistic函數
● Tanh函數
● ReLu函數
● 損失函數和輸出單元
● 損失函數的選擇
● 均方誤差損失函數
● 交叉熵損失函數
● 輸出單元的選擇
● 線性單元
● Sigmoid單元
● Softmax單元
● 參考文獻
一.神經網絡前言
從本章起,我們将正式開始介紹神經網絡模型,以及學習如何使用TensorFlow實作深度學習算法。人工神經網絡(簡稱神經網絡)在一定程度上受到了生物學的啟發,期望通過一定的拓撲結構來模拟生物的神經系統,是一種主要的連接配接主義模型(人工智能三大主義:符号主義、連接配接主義和行為主義)。本章我們将從最簡單的神經網絡模型感覺器模型開始介紹,首先了解一下感覺器模型(單層神經網絡)能夠解決什麼樣的問題,以及它所存在的局限性。為了克服單層神經網絡的局限性,我們必須拓展到多層神經網絡,圍繞多層神經網絡我們會進一步介紹激活函數以及反向傳播算法等。本章的内容是深度學習的基礎,對于了解後續章節的内容非常重要。
深度學習的概念是從人工神經網絡的研究中發展而來的,早期的感覺器模型隻能解決簡單的線性分類問題,後來發現通過增加網絡的層數可以解決類似于“異或問題”的線性不可分問題,這種多層的神經網絡又被稱為多層感覺器。對于多層感覺器,我們使用BP算法進行模型的訓練[1],但是我們發現BP算法有着收斂速度慢,以及容易陷入局部最優等缺點,導緻BP算法無法很好的訓練多層感覺器。另外,當時使用的激活函數也存在着梯度消失的問題,這使得人工神經網絡的發展幾乎陷入了停滞狀态。為了讓多層神經網絡能夠訓練,學者們探索了很多的改進方案,直到2006年Hinton等人基于深度置信網絡(DBN)提出了非監督貪心逐層訓練算法,才讓這一問題的解決有了希望,而深度學習的浪潮也由此掀起。
本章内容主要包括五個部分,第一部分我們介紹一下神經網絡的基本結構,從基本的感覺器模型到多層的神經網絡結構;第二部分介紹神經網絡中常用的激活函數;第三部分介紹損失函數和輸出單元的選擇;第四部分介紹神經網絡模型中的一個重要的基礎知識——反向傳播算法;最後我們使用TensorFlow搭建一個簡單的多層神經網絡,實作mnist手寫數字的識别。
二、神經網絡
1. 感覺機模型
感覺器(Perceptron)是一種最簡單的人工神經網絡,也可以稱之為單層神經網絡,如圖1所示。感覺器是由Frank Rosenblatt在1957年提出來的,它的結構很簡單,輸入是一個實數值的向量,輸出隻有兩個值:1或-1,是一種兩類線性分類模型。
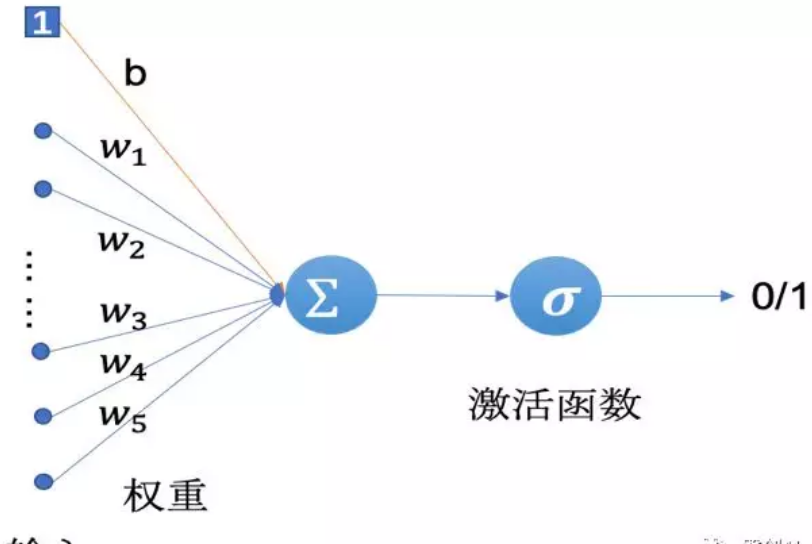
圖1 感覺器模型
如圖3-1所示,感覺器對于輸入的向量先進行了一個權重求和的操作,得到一個中間值,假設該值為,則有:
接着再經過一個激活函數得到最終的輸出,該激活函數是一個符号函數:
公式1中的可以看做是一個門檻值(我們通常稱之為偏置項),當輸入向量的權重和大于該門檻值時(兩者之和)感覺器的輸出為1,否則輸出為-1。
2. 多層神經網絡
感覺器隻能解決線性可分的問題,以邏輯運算為例:
感覺器可以解決邏輯“與”和邏輯“或”的問題,但是無法解決“異或”問題,因為“異或”運算的結果無法使用一條直線來劃分。為了解決線性不可分的問題,我們需要引入多層神經網絡,理論上,多層神經網絡可以拟合任意的函數(本書配套的GitHub項目中有相關資料供參考)。
與單層神經網絡相比,多層神經網絡除了有輸入層和輸出層以外,還至少需要有一個隐藏層,如圖3所示是含有一個隐藏層的兩層神經網絡:
為了更直覺的比較一下單層神經網絡和多層神經網絡的差别,我們利用TensorFlow PlayGround來示範兩個例子。TensorFlowPlayGround是Google推出的一個深度學習的可視化的示範平台:http://playground.tensorflow.org/。
我們首先看一個線性可分的例子,如圖4所示。圖的右側是資料可視化後的效果,資料是能夠用一條直線劃分的。從圖中可以看到,我們使用了一個單層神經網絡,輸入層有兩個神經元,輸出層隻有一個神經元,并且使用了線性函數作為激活函數。
我們點選開始訓練的按鈕,最終的分類結果如圖5所示:
在上面的例子裡我們使用單層神經網絡解決了一個線性可分的二分類問題,接下來我們再看一個線性不可分的例子,如圖6所示:
在這個例子裡,我們使用了一組線性不可分的資料。為了對這組資料進行分類,我們使用了一個含有一層隐藏層的神經網絡,隐藏層有四個神經元,并且使用了一個非線性的激活函數ReLU。要想對線性不可分的資料進行分類,我們必須引入非線性的因素,即非線性的激活函數,在下一小節裡,我們會再介紹一些常用的激活函數。
最終的分類結果如圖7所示。
感興趣的讀者可以嘗試使用線性的激活函數,看會是什麼樣的效果,還可以嘗試其它的資料,試着增加網絡的層數和神經元的個數,看看分别對模型的效果會産生什麼樣的影響。
三.激活函數
為了解決非線性的分類或回歸問題,我們的激活函數必須是非線性的函數,另外我們使用基于梯度的方式來訓練模型,是以激活函數也必須是連續可導的。
1. Logistic函數
Logistic函數(又稱為sigmoid函數)的數學表達式和函數圖像如圖8所示:
Logistic函數在定義域上單調遞增,值域為,越靠近兩端,函數值的變化越平緩。因為Logistic函數簡單易用,以前的神經網絡經常使用它作為激活函數,但是由于Logistic函數存在一些缺點,使得現在的神經網絡已經很少使用它作為激活函數了。它的缺點之一是容易飽和,從函數圖像可以看到,Logistic函數隻在坐标原點附近有很明顯的梯度變化,其兩端的函數變化非常平緩,這會導緻我們在使用反向傳播算法更新參數的時候出現梯度消失的問題,并且随着網絡層數的增加問題會越嚴重。
2. Tanh函數
Tanh函數(雙曲正切激活函數)的數學表達式和函數圖像如圖9所示:
Tanh函數很像是Logistic函數的放大版,其值域為。在實際的使用中,Tanh函數要優于Logistic函數,但是Tanh函數也同樣面臨着在其大部分定義域内都飽和的問題。
3. ReLu函數
ReLU函數(又稱修正線性單元或整流線性單元)是目前最受歡迎,也是使用最多的激活函數,其數學表達式和函數圖像如圖10所示:
ReLU激活函數的收斂速度相較于Logistic函數和Tanh函數要快很多,ReLU函數在軸左側的值恒為零,這使得網絡具有一定的稀疏性,進而減小參數之間的依存關系,緩解過拟合的問題,并且ReLU函數在軸右側的部分導數是一個常數值1,是以其不存在梯度消失的問題。但是ReLU函數也有一些缺點,例如ReLU的強制稀疏處理雖然可以緩解過拟合問題,但是也可能産生特征屏蔽過多,導緻模型無法學習到有效特征的問題。
除了上面介紹的三種激活函數以外,還有很多其它的激活函數,包括一些對ReLU激活函數的改進版本等,但在實際的使用中,目前依然是ReLU激活函數的效果更好。現階段激活函數也是一個很活躍的研究方向,感興趣的讀者可以去查詢更多的資料,包括本書GitHub項目中給出的一些參考資料等。
四.損失函數和輸出單元
損失函數(LossFunction)又稱為代價函數(Cost Function),它是神經網絡設計中的一個重要部分。損失函數用來表征模型的預測值與真實類标之間的誤差,深度學習模型的訓練就是使用基于梯度的方法最小化損失函數的過程。損失函數的選擇與輸出單元的選擇也有着密切的關系。
1. 損失函數的選擇
1.1 均方誤差損失函數
均方誤差(MeanSquared Error,MSE)是一個較為常用的損失函數,我們用預測值和實際值之間的距離(即誤差)來衡量模型的好壞,為了保證一緻性,我們通常使用距離的平方。在深度學習算法中,我們使用基于梯度的方式來訓練參數,每次将一個批次的資料輸入到模型中,并得到這批資料的預測結果,再利用這批預測結果和實際值之間的距離更新網絡的參數。均方誤差損失函數将這一批資料的誤差的期望作為最終的誤內插補點,均方誤差的公式如下:
上式中為樣本資料的實際值,為模型的預測值。為了簡化計算,我們一般會在均方誤差的基礎上乘以,作為最終的損失函數:
1.2交叉熵損失函數
交叉熵(Cross Entropy)損失函數使用訓練資料的真實類标與模型預測值之間的交叉熵作為損失函數,相較于均方誤差損失函數其更受歡迎。假設我們使用均方誤差這類二次函數作為代價函數,更新神經網絡參數的時候,誤差項中會包含激活函數的偏導。在前面介紹激活函數的時候我們有介紹,Logistic等激活函數很容易飽和,這會使得參數的更新緩慢,甚至無法更新。交叉熵損失函數求導不會引入激活函數的導數,是以可以很好地避免這一問題,交叉熵的定義如下:
上式中為樣本資料的真實分布,為模型預測結果的分布。以二分類問題為例,交叉熵損失函數的形式如下:
上式中為真實值,為預測值。對于多分類問題,我們對每一個類别的預測結果計算交叉熵後求和即可。
2. 輸出單元的選擇
2.1 線性單元
線性輸出單元常用于回歸問題,當輸出層采用線性單元時,收到上一層的輸出後,輸出層輸出一個向量。線性單元的一個優勢是其不存在飽和的問題,是以很适合采用基于梯度的優化算法。
2.2 Sigmoid單元
Sigmoid輸出單元常用于二分類問題,Sigmoid單元是線上性單元的基礎上,增加了一個門檻值來限制其有效機率,使其被限制在區間之中,線性輸出單元的定義為:
上式中是Sigmoid函數的符号表示,其數學表達式在3.2.1節中有介紹。
2.3 Softmax單元
Softmax輸出單元适用于多分類問題,可以将其看作是Sigmoid函數的擴充。對于Sigmoid輸出單元的輸出,我們可以認為其值為模型預測樣本為某一類的機率,而Softmax則需要輸出多個值,輸出值的個數對應分類問題的類别數。Softmax函數的形式如下:
我們以一個簡單的圖示來解釋Softmax函數的作用,如圖3-11所示。原始輸出層的輸出為,,,增加了Softmax層後,最終的輸出為:
上式中、和的值可以看做是分類器預測的結果,值的大小代表分類器認為該樣本屬于該類别的機率,
需要注意的是,Softmax層的輸入和輸出的次元是一樣的,如果不一緻,可以通過在Softmax層的前面添加一層全連接配接層來解決問題。
接下來将介紹第四部分:神經網絡模型中的一個重要的基礎知識——反向傳播算法;與第五部分:使用TensorFlow搭建一個簡單的多層神經網絡,實作mnist手寫數字的識别。
原文釋出時間為:2018-11-2
本文作者:磐石001
本文來自雲栖社群合作夥伴“
磐創AI”,了解相關資訊可以關注“
”。