一、python實作連結清單冒泡排序
- 冒泡排序的概念:冒泡排序是一種交換排序,它的基本思想是:兩兩比較相鄰記錄的關鍵字,如果反序則交換,直至沒有反序的記錄為止。因為按照該算法,每次比較會将目前未排序的記錄序列中最小的關鍵字移至未排序的記錄序列最前(或者将目前未排序的記錄序列中最大的關鍵字移至未排序的記錄序列最後),就像冒泡一樣,故以此為名。
- 冒泡排序算法的算法描述如下:
-- 比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。
-- 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。這步做完後,最後的元素會是最大的數。
-- 針對所有的元素重複以上的步驟,除了最後一個。
-- 持續每次對越來越少的元素重複上面的步驟,直到沒有任何一對數字需要比較。
1、基本的冒泡排序實作:
li = [23, 43, 1, 2, 4, 5, 253]
def bubble(li):
if not len(li):
return
count = 0
for i in range(len(li)):
for j in range(len(li) - 1):
count+=1
if li[i] < li[j]:
li[i], li[j] = li[j], li[i]
print(count)
return li
ret_li = bubble(li)
print(ret_li)
42 //循環的次數
[1, 2, 4, 5, 23, 43, 253] //排序結果
2、基本優化
這種方法利用了雙重循環,會造成不必要的比較,是以優化一下,可以考慮從尾部開始,這樣可以将以排好序的部分不再檢查
def bubble(li):
if not len(li):
return
count = 0
for i in range(len(li)):
j = len(li) - 1
while j > i:
count +=1
if li[j] < li[j - 1]:
li[j], li[j - 1] = li[j - 1], li[j]
j -= 1
print(count)
return li
ret_li = bubble(li)
print(ret_li)
21//循環的次數
[1, 2, 4, 5, 23, 43, 253] //排序結果
3、進一步優化
通過設定flag來判斷某次循環是否沒有出現位置交換,沒有交換就說明排序已完成
def bubble(li):
if not len(li):
return
count = 0
for i in range(len(li)):
flag = False
j = len(li) - 1
while j > i:
count += 1
if li[j] < li[j - 1]:
li[j], li[j - 1] = li[j - 1], li[j]
flag = True
j -= 1
if not flag:
print(count)
return li
return li
ret_li = bubble(li)
print(ret_li)
20 //循環次數
二、二叉樹的順序周遊
-
二叉樹是有限個元素的集合,該集合或者為空、或者有一個稱為根節點(root)的元素及兩個互不相交的、分别被稱為左子樹和右子樹的二叉樹組成。
-- 二叉樹的每個結點至多隻有二棵子樹(不存在度大于2的結點),二叉樹的子樹有左右之分,次序不能颠倒。
-- 二叉樹的第i層至多有2^{i-1}個結點
-- 深度為k的二叉樹至多有2^k-1個結點;
-- 對任何一棵二叉樹T,如果其終端結點數為N0,度為2的結點數為N2,則N0=N2+1
-
二叉樹有三種周遊方式:先序周遊,中序周遊,後續周遊 即:先中後指的是通路根節點的順序 eg:先序 根左右 中序 左根右 後序 左右根
周遊總體思路:将樹分成最小的子樹,然後按照順序輸出
#實作樹結構的類,樹的節點有三個私有屬性 左指針 右指針 自己的值
class Node():
def __init__(self,data =None,left=None,right = None):
self._data = data
self._left = left
self._right = right
#先序周遊 周遊過程 根左右
def pro_order(tree):
if tree == None:
return False
print(tree._data)
pro_order(tree._left)
pro_order(tree._right)
#後序周遊 周遊過程 左右根
def pos_order(tree):
if tree == None:
return False
# print(tree.get_data())
pos_order(tree._left)
pos_order(tree._right)
print(tree._data)
#中序周遊 周遊過程 左根右
def mid_order(tree):
if tree == None:
return False
# print(tree.get_data())
mid_order(tree._left)
print(tree._data)
mid_order(tree._right)
#層次周遊
def row_order(tree):
# print(tree._data)
queue = []
queue.append(tree)
while True:
if queue==[]:
break
print(queue[0]._data)
first_tree = queue[0]
if first_tree._left != None:
queue.append(first_tree._left)
if first_tree._right != None:
queue.append(first_tree._right)
queue.remove(first_tree)
if __name__ == '__main__':
tree = Node('A',Node('B',Node('D'),Node('E')),Node('C',Node('F'),Node('G')))
pro_order(tree)
mid_order(tree)
pos_order(tree)
row_order(tree)
三、python實作順序表的快排
1、快排的介紹:
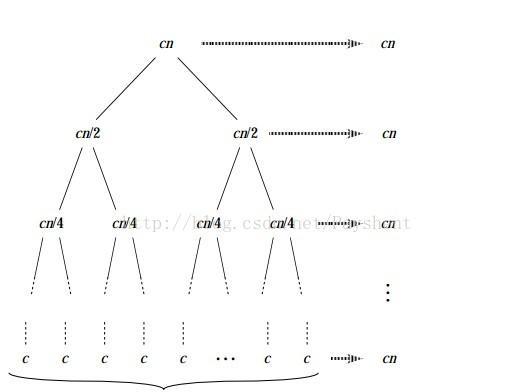
快速排序采用的思想是分治思想,先簡單的介紹一下分治的思想。分治算法的基本思想是将一個規模為N的問題分解為K個規模較小的子問題,這些子問題互相獨立且與原問題性質相同。求出子問題的解,就可以得到原問題的解。下面這張圖會說明分治算法是如何進行的:将cn分成了兩個cn/2,轉而分成了cn/4,cn/8......我們通過這樣一層一層的求解規模小的子問題,将其合并之後就能求出原問題的解。
圖解.jpg
2、快排的基本思路是:
在待排序的序列中選取一個值作為一個基準值,按照這個基準值得大小将這個序列劃分成兩個子序列,基準值會在這兩個子序列的中間,一邊是比基準小的,另一邊就是比基準大的。這樣快速排序第一次排完,我們選取的這個基準值就會出現在它該出現的位置上。這就是快速排序的單趟算法,也就是完成了一次快速排序。然後再對這兩個子序列按照同樣的方法進行排序,直到隻剩下一個元素或者沒有元素的時候就停止,這時候所有的元素都出現在了該出現的位置上。
附圖:快排的圖解
快排.jpg
3、快排的特點
快速排序之所比較快,因為相比冒泡排序,每次交換是跳躍式的。每次排序的時候設定一個基準點,将小于等于基準點的數全部放到基準點的左邊,将大于等于基準點的數全部放到基準點的右邊。這樣在每次交換的時候就不會像冒泡排序一樣每次隻能在相鄰的數之間進行交換,交換的距離就大的多了。是以總的比較和交換次數就少了,速度自然就提高了。當然在最壞的情況下,仍可能是相鄰的兩個數進行了交換。是以快速排序的最差時間複雜度和冒泡排序是一樣的都是O(N2),它的平均時間複雜度為O(NlogN)。其實快速排序是基于一種叫做“二分”的思想。
4、快排的代碼實作
def quick_sort(li):
if len(li) <= 1:
return li
base_value = li[len(li) // 2]
left_part = [item for item in li if item < base_value]
right_part = [item for item in li if item > base_value]
eq_part = [item for item in li if item == base_value]
return quick_sort(left_part) + eq_part + quick_sort(right_part)
print(quick_sort(li = [23, 43, 1, 2, 4, 5, 253]))
簡潔版的快排,兩種代碼其實是一樣的
def quick_sort(li):
if len(li) <= 1:
return li
return quick_sort([item for item in li[1:] if item < li[0]])+ li[0:1] + quick_sort([item for item in li[1:] if item > li[0]])
print(quick_sort(li = [23, 43, 1, 2, 4, 5, 253]))