前言
B+樹是1970年
Rudolf Bayer
教授在
《Organization and Maintenance of Large Ordered Indices》
一文中提出的[1]。它采用多叉樹結構,降低了索引結構的深度,避免傳統二叉樹結構中絕大部分的随機通路操作,進而有效減少了磁盤磁頭的尋道次數,降低了外存通路延遲對性能的影響。它保證樹節點中鍵值對的有序性,進而控制search/insert/delete/update操作的時間複雜度在
O(log(n))
的範圍内。鑒于上述優勢,B+樹作為索引結構的構模組化塊,被廣泛應用在大量資料庫系統和存儲系統中,其中就包括MySQL。
索引結構作為影響系統性能的關鍵因素之一,對資料庫系統在高并發場景下的性能表現具有重大的影響。從1970年B+樹提出至今,學術界有大量論文嘗試優化B+樹在多線程場景下的性能,這些文章被廣泛發表在資料庫/系統領域頂級會議
VLDB/SIGMOD/EuroSys
上。然而,由于過長的時間跨度(1970s-2010s,40多年時間),目前網絡上缺乏讨論B+樹并發機制的較為系統的分析文章,尤其在中文文章方面。本文嘗試選取不同時間點上幾個具有代表性的研究工作,分析B+樹并發控制機制的發展過程,探讨B+樹并發機制在MySQL中的發展及優化。由于篇幅和時間限制,本文的部分觀點可能尚不完善,讀者可根據文章末尾的引用論文,深入閱讀相關工作。
- B+樹的資料結構及基礎操作
- B+樹并發控制機制的基本要求
- B+樹并發控制機制的發展曆程(從1970s至今)
- Mysql5.7的B+樹并發控制機制
- Lock-Free B+樹 & 總結
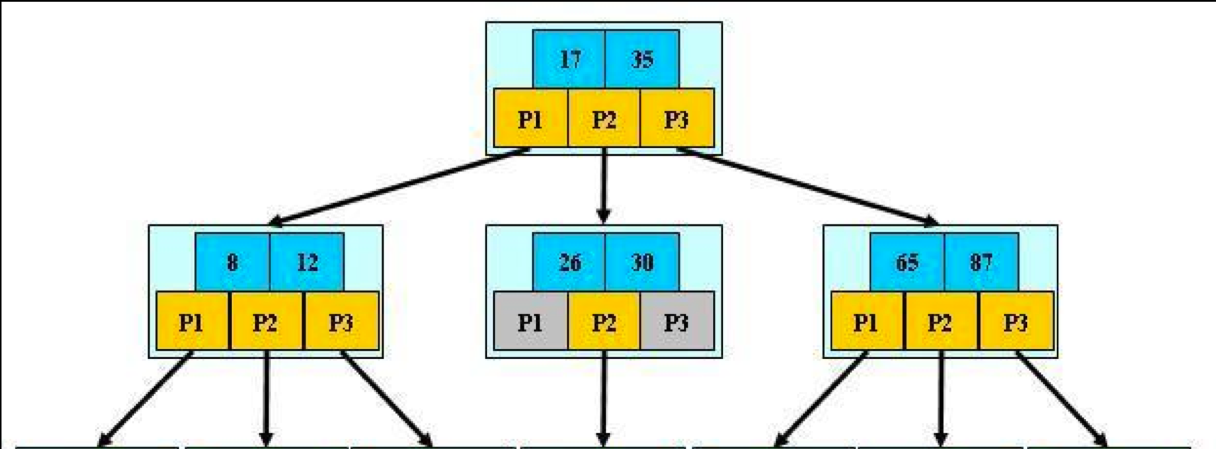
一棵傳統的B+樹需要滿足以下幾點要求:
- 從根節點到葉節點的所有路徑都具有相同的長度
- 所有資料資訊都存儲在葉節點上,非葉節點僅作為葉節點的索引存在
- 根結點至少擁有兩個鍵值對
- 每個樹節點最多擁有M個鍵值對
- 每個樹節點(除了根節點)擁有至少M/2個鍵值對
一棵傳統的B+需要支援以下操作:
- 單鍵值操作:Search/Insert/Update/Delete(下文以Search/Insert操作為例,其它操作的實作相似)
- 範圍操作:Range Search
由于篇幅所限,本文假設讀者對B+樹的基礎結構和操作原理有一定的了解,僅對B+樹的基本結構和操作做簡單介紹,有需求的讀者可根據引用[1]的文章自行閱讀。
按照筆者的了解,正确的B+樹并發控制機制需要滿足以下幾點要求:
-
正确的讀操作
- R.1 不會讀到一個處于中間狀态的鍵值對:讀操作通路中的鍵值對正在被另一個寫操作修改
- R.2 不會找不到一個存在的鍵值對:讀操作正在通路某個樹節點,這個樹節點上的鍵值對同時被另一個寫操作(分裂/合并操作)移動到另一個樹節點,導緻讀操作沒有找到目标鍵值對
-
正确的寫操作
- W.1 兩個寫操作不會同時修改同一個鍵值對
-
無死鎖
- D.1 不會出現死鎖:兩個或多個線程發生永久堵塞(等待),每個線程都在等待被其他線程占用并堵塞了的資源
不管B+樹使用的是基于鎖的并發機制還是Lock-Free的并發機制,都必須滿足上述需求。在下文中,本文将針對不同的并發機制,分别闡述它們是如何滿足上述要求,并達到了什麼樣的優化效果。
本文使用的一些标記
首先,介紹本文僞代碼中需要使用的一些标記。
-
SL (Shared Lock)
-
SU (Shared Unlock)
-
XL (Exclusive Lock)
-
XU (Exclusive Unlock)
-
SXL (Shared Exclusive Lock)
-
SXU (Shared Exclusive Unlock)
-
R.1/R.2/W.1/D.1
-
safe nodes
btr_cur_will_modify_tree()
基礎并發控制機制(MySQL5.6)
MySQL5.6以及之前的版本采用了一種較為基礎的并發機制:它采用了兩種粒度的鎖:(1)index粒度的S/X鎖;(2)page粒度的S/X鎖(本文等同于樹節點粒度)。前者被用來控制對樹結構通路及修改操作的沖突,後者被用來控制對資料頁通路及修改操作的沖突。下文将以僞代碼的形式詳細分析讀寫操作的過程。
/* Algorithm1. 讀操作 */
1. SL(index)
2. Travel down to the leaf node
3. SL(leaf)
4. SU(index)
5. Read the leaf node
6. SU(leaf)
在
Algorithm 1
中,讀操作首先對整個B+樹加S鎖(
step1
),其次通路樹結構直到對應的葉節點(
step2
),接着對葉節點的page加S鎖(
step3
),再釋放index的S鎖(
step4
),然後通路葉節點的内容(
step5
),最後釋放葉節點的S鎖(
step6
)。從上述步驟可以看出,讀操作通過index的S鎖,避免在通路到樹結構的過程中樹結構被其它寫操作所修改,進而滿足R.2的正确性要求。其次,讀操作到達葉節點後先申請葉節點頁的鎖,再釋放index的鎖,進而避免在通路具體的鍵值對資訊時資料被其它寫操作所修改,滿足R.1的正确性要求。由于讀操作在通路樹結構的過程中對B+樹加的是S鎖,是以其它讀操作可以并行通路樹結構,減少了讀-讀操作之間的并發沖突。
/* Algorithm2. 悲觀寫操作 */
1. XL(index)
2. Travel down to the leaf node
3. XL(leaf) /* lock prev/curr/next leaves */
4. Modify the tree structure
5. XU(index)
6. Modify the leaf node
7. XU(leaf)
因為寫操作可能會修改整個樹結構,是以需要避免兩個寫操作同時通路B+樹。為了解決這個問題,
Algorithm 2
采用了一種較為悲觀的方案。每個寫操作首先對B+樹加X鎖(
step1
),進而阻止了其它讀寫操作在這個寫操作執行過程中通路B+樹,避免它們通路到一個錯誤的中間狀态。其次,它周遊樹結構直到對應的葉節點(
step2
),并對葉節點的page加X鎖(
step3
)。接着,它判斷該操作是否會引發split/merge等修改樹結構的操作。如果是,它就修改整個樹結構(
step4
)後再釋放index的鎖(
step5
)。最後,它在修改葉節點的内容(
step6
)後釋放了葉節點的X鎖(
step7
)。雖然悲觀寫操作通過索引粒度的互斥鎖滿足了W.1的正确性要求,然而因為寫操作在通路樹結構的過程中對B+樹加的是X鎖,是以它會堵塞其它的讀/寫操作,這在高并發場景下會導緻糟糕的多線程擴充性。這是否存在可優化的空間呢?請接着看下文。
/* Algorithm3. 樂觀寫操作 */
1. SL(index)
2. Travel down to the leaf node
3. XL(leaf)
4. SU(index)
5. Modify the leaf node
6. XU(leaf)
實際上,因為每一個樹節點頁可以容納大量的鍵值對資訊,是以B+樹的寫操作在多數情況下并不會觸發split/merge等修改樹結構的操作。是以,相比于
Algorithm 2
中的悲觀思想,
Algorithm 3
中采用了一種樂觀思想,即假設大部分寫操作并不會修改樹結構。在
Algorithm 3
中,寫操作的整個過程與
Algorithm 1
大緻相同,它在通路樹結構過程中持有樹結構的S鎖,進而支援其它讀/樂觀寫操作同時通路樹結構。
Algorithm 3
與
Algorithm 1
主要的差別在于寫操作對葉節點持有X鎖。在MySQL5.6中,B+樹往往優先執行樂觀寫操作,隻有樂觀寫操作失敗才會執行悲觀寫操作,進而減少了操作之間的沖突和堵塞。不管是悲觀寫操作還是樂觀寫操作,它都通過索引粒度或者頁粒度的鎖避免互相之間修改相同的資料,是以滿足W.1的正确性要求。
對于死鎖問題,MySQL5.6采用的是“從上到下,從左到右”的加鎖順序,不會出現兩個線程加鎖順序成環的現象,是以不會出現死鎖的情況,滿足D.1的正确性要求。
隻鎖住被修改的分支
雖然MySQL5.6采用樂觀寫操作減少了線程間的沖突,但是它的主要問題在于:即使其它讀寫操作通路的是樹結構的不同分支,在實際執行過程中不會産生互相間的影響,但是悲觀寫操作依然會堵塞其它所有讀/寫操作,直到樹結構修改完成,這導緻了過高的堵塞開銷。是否存在一種并發機制,它隻鎖住B+樹中被修改的分支,而不是鎖住整個樹結構呢?答案是肯定的,
《B-trees in a system with multiple users》
在1976年就已經提出了一種可行的方案[2]。
與MySQL5.6不同,
Algorithm 4-5
中的算法不再使用索引粒度的S/X鎖,而隻使用樹節點粒度的S/X鎖。因為樹節點粒度鎖的支援,當修改樹結構時,寫操作不再隻是粗暴地對整個索引結構加鎖,而隻對修改的分支加鎖。首先,我們先看讀操作的具體實作。
/* Algorithm4. 讀操作 */
1. current <= root
2. SL(current)
3. While current is not leaf do {
4. SL(current->son)
5. SU(current)
6. current <= current->son
7. }
8. Read the leaf node
9. SU(current)
Algorithm 4
中,讀操作從根節點出發,首先持有根節點的S鎖(
step1-2
)。在(
step3-7
)的過程中,讀操作先獲得子節點的S鎖,再釋放父節點的S鎖,這個過程反複執行直到找到某個葉節點。最後,它在讀取葉節點的内容(
step8
)後釋放了葉節點的S鎖(
step9
)。因為讀操作在持有子節點的鎖後才釋放父節點的鎖,是以不會讀到一個正在修改的樹節點,不會在定位到某個子節點後子節點的鍵值對被移動到其它節點,是以能滿足R.1/R.2的正确性要求。
/* Algorithm5. 寫操作 */
1. current <= root
2. XL(current)
3. While current is not leaf do {
4. XL(current->son)
5. current <= current->son
6. If current is safe do {
7. /* Unlocked ancestors on stack. */
8. XU(locked ancestors)
9. }
10. }
11. /* Already lock the modified branch. */
12. Modify the leaf and upper nodes
13. XU(current) and XU(locked ancestors)
Algorithm 5
中,寫操作同樣從根節點出發,首先持有根節點的X鎖(
step1-2
)。在
step3
到
step10
的過程中,寫操作先獲得子節點的X鎖,然後判斷子節點是否是一個安全節點(操作會引起該節點的分裂/合并等修改樹結構的操作)。如果子節點是安全節點,寫操作立即釋放祖先節點(可能包含多個節點)的X鎖,否則就會暫時保持父節點的鎖,這個過程反複執行直到找到某個葉節點。當到達了葉節點後,寫操作就已經持有了修改分支上所有樹節點的X鎖,進而避免其它讀/寫操作通路該分支(
step11
),滿足W.1的正确性要求。最後,它在修改這個分支的内容(
step12
)後釋放了分支的鎖(
step13
)。
對于死鎖問題,
Algorithm 4-5
同樣采用的是“從上到下”的加鎖順序,滿足D.1的正确性要求。
值得注意的是,
Algorithm 4-5
中提出的并發機制被使用到MySQL5.7中,詳細情況将在後文中說明。
SX鎖橫空出世
Algorithm 4-5
提出的并發機制的主要問題在于它其實依然采用了一種較為悲觀的思想:寫操作在到達被修改分支之前,對途徑的樹節點加的是X鎖,這在一定程度上阻塞了其它操作通路對應的樹節點。當這個寫操作需要頻繁将樹節點從磁盤讀取到記憶體産生較高的IO延遲時,這個堵塞開銷會更高。如前文所述,在大部分情況下,寫操作并不會修改途徑的非葉節點,是以不會對通路相同節點的讀操作産生影響。但是,如果寫操作到達某個子節點時發現子節點是unsafe的,它必須一直持有父節點的鎖,否則父節點可能已被其它寫操作所修改。是以出現一個問題,是否存在一種位于S鎖與X鎖之間的SX鎖,它可以堵塞其它的SX/X加鎖操作(寫操作),但可以允許S加鎖操作(讀操作),并且當它确定要修改該節點時可更新為X鎖堵塞其它讀寫操作。
Rudolf Bayer
教授于1977年在
《Concurrency of operations on B -trees》
一文中提出了SX鎖,SX鎖被使用到了MySQL5.7中,詳細情況将在後文中說明。此外,這篇文章提出了先嘗試樂觀寫操作,再執行悲觀寫操作的優化政策,如前文所述,該政策已經應用到MySQL5.6中。
/* Algorithm6. 寫操作 */
1. current <= root
2. SXL(current)
3. While current is not leaf do {
4. SXL(current->son)
5. current <= current->son
6. If current is safe do {
7. /* Unocked ancestors on stack. */
8. SXU(locked ancestors)
9. }
10. }
11. XL(modified nodes) /* SX->X, top-to-down*/
12. /* Already lock the modified branch. */
13. Modify the leaf and upper nodes
13. XU(current) and XU(locked ancestors)
因為SX鎖隻與寫操作有關,是以本章節使用了與
Algorithm 4
相同的讀操作,隻介紹不同的寫操作。
Algorithm 6
與在
Algorithm 5
十分相似,主要的差別在于,
Algorithm 6
step2,4,8
中使用SX鎖取代了X鎖。到達某個葉節點後,它再将修改分支上的SX鎖更新為X鎖。這樣做的好處在于,在寫操作将影響分支上的鎖更新為X鎖前,所有讀操作都可以通路被這個寫操作通路過的非葉節點,進而減少了線程之間的沖突。由于SX鎖的存在,不會出現多個寫操作修改同一個分支的情況,進而滿足了W.1的正确性要求。
鎖,請你使用地盡可能少一些
前文中的并發控制機制在很大程度上減少了線程間的沖突,但是依然存在一個問題:不論讀/寫操作,它們在通路一個樹節點前都需要對樹節點加S/SX/X鎖。頻繁加鎖産生的開銷,在核數越來越多/硬體性能越來越強的今天,開始慢慢成為一個不可忽略的開銷,尤其在記憶體資料庫/記憶體系統中。發表在2001年資料庫領域頂級會議
VLDB
的文章
《Cache-Conscious Concurrency Control of Main-Memory Indexes on Shared-Memory Multiprocessor Systems》
詳細說明了這個問題[6]。
頻繁加鎖操作在多核處理器上會産生
Coherence Cache Miss
過高的問題。以上圖為例,假設有4個處理器(p1/p2/p3/p4),每個處理器分别有自己的private cache(c1/c2/c3/c4)。為了便于說明,同樣假設有4個線程(p1/p2/p3/p4),與處理器一一綁定。下文中的n1/n2/n3/n4/n5/n6/n7可以指的是樹節點的鎖,也可以指代樹節點,兩者在下文叙述中等價。下面開始說明為什麼頻繁加鎖會引入較高的Coherence Cache Miss開銷:
- a. p1通路樹節點n1/n2/n4,然後将它們放在緩存c1;
- b. p2通路樹節點n1/n2/n5,然後将它們放在緩存c2;
- c. p2修改的S鎖會導緻緩存c1中的n1/n2失效;
- d. 注意即使緩存c1中有足夠大的空間,這些緩存缺失操作依然會發生;
- e. p3通路樹節點n1/n2/n5,然後導緻緩存c2中的n1/n2失效;
- f. p4通路樹節點n1/n3/n7,然後導緻緩存c3中的n1/n3失效;
如上圖所示,不論哪個線程通路樹結構,由于它在通路每個樹節點時都需要修改對應的樹節點鎖,這會導緻其它private cache裡的資料失效,帶來過高的緩存一緻性開銷。随着多核處理器的發展,以NUMA架構為基礎的多核處理器産品在資料中心中被廣泛使用,而這類産品上的緩存一緻性開銷将會成為更加嚴重的問題。為了更加明确地說明這一點,本文從Intel官方資料中引用了部分資料[5]。
上文分别列舉了E7-4800和E5-4600兩款處理器的參數,我們可以看到跨socket的通路延遲高達200-300ns。大家都知道,通路一次記憶體的操作僅為50-100ns,而加鎖操作導緻的跨socket同步操作帶來的延遲遠高于訪存操作。當系統中存在大量cache coherence miss時,勢必會提高處理器/總線的資源消耗,産生較高的延遲開銷,這在記憶體資料庫/記憶體系統中更是一個不可忽略的問題。那是否可以減少加鎖的頻率,在保證正确性的基礎上減少鎖操作帶來的開銷呢?答案依然是肯定的。
前文中所述的并發機制,往往采用自頂向下的加鎖政策,在安全地擷取到子節點的鎖後釋放父節點的鎖。然而我們很容易發現,這種加鎖方式依然是十分悲觀的:大部分擷取到的鎖其實是無意義的,尤其在樹的上層,因為離根節點越近的樹節點被更新的機率越低。是以,如果存在一種自底向上加鎖的政策,隻有在樹節點分裂或者合并或者删除的情況下向上加鎖,隻對被修改的樹節點加鎖,就可以在很大程度上減少加鎖的範圍和頻率,進而提高B+樹的多線程擴充性。為了實作這個目标,我們首先需要支援在不持有鎖的狀态下從根節點通路到葉節點的功能。想知道這個目标是如何實作的,請耐下性子接着看下文 :D。
Blink樹,對後世影響深遠的多線程B+樹
1981年,資料庫領域頂級期刊
TODS
上發表了一篇文章
《Efficient locking for concurrent operations on B-trees》
[4],介紹
Blink樹`這一簡單有效的多線程B+樹。由于年代深遠,Blink-Tree當時假設的計算機模型與現在主流的計算機并不相同。筆者對其的總結是:Blink樹假設通路樹節點的讀寫操作是原子性的,讀操作不會讀到寫操作修改到一半的狀态(即已滿足R.1正确性要求),但寫操作之間修改同一份資料時會出現沖突。具體的計算機模型讀者可查閱[4]這篇論文,這一假設存在的問題會在後文中得到解決。Blink樹提出為每一個樹節點配置一個右指針。别小看這麼簡單的一個設計,它的出現使得在無鎖狀态下自頂向下的通路政策+自底向上的加鎖政策成為可能,對後續多種多線程B+樹的設計産生深遠的影響。
/* Algorithm7. 讀操作 */
1. current <= root
2. While current is not leaf do {
3. current <= scanNode(current, v)
4. current <= current->son
5. }
6. /* Keep move right if necessary. */
7. /* Deal with the leaf node. */
/* scanNode函數 */
8. Func scanNode(node* t, int v) {
9. If t->next->key[0] <= v do
10. t <= scanNode(t->next, v)
11. return t;
12. }
Algorithm 7
中,讀操作從根節點出發,周遊整個樹結構,直到找到某個葉子節點(
step1-5
)。注意在這個過程中,讀操作并不持有鎖。
Algorithm 7
的特殊之處在于在每到達一個子節點後,它都會調用
scanNode
函數,這個函數就是Blink樹的精髓所在。因為讀操作在周遊樹結構的過程中不持有鎖,這導緻它通路的某個樹節點可能被其它寫操作所分裂或者删除。當讀操作準備通路某個子節點時,這時這個子節點被其它寫操作分裂,可能導緻目标鍵值對被移動到子節點的兄弟節點,導緻讀操作找不到一個其實存在的鍵值對,就發生了R.2錯誤。當讀操作通路某個子節點的過程中,這個子節點被其它寫操作删除,那麼這個讀操作可能會發生dangling pointer的錯誤。
前文提到,Blink樹提出為每一個樹節點配置一個右指針,這個右指針為讀操作提供了另一種方式去通路子節點的右兄弟節點。Blink樹規定樹的分裂操作順序必然是從左至右,是以目标鍵值對隻有可能被分裂到子節點的右兄弟節點。在(
step8-12
)中說明了
scanNode
的實作。大緻的過程就是讀操作會判斷子節點的右兄弟節點的最小值是否大于它正在查找的目标鍵值,如果不是說明目标鍵值對在右兄弟節點或者更右邊的節點,指針就會往右走,直到找到某個右兄弟節點的最小值大于目标鍵值。是以,右指針的存在幫助讀操作能定位到真實存在的所有鍵值對,進而滿足R.2的正确性要求。
對于删除操作,年代久遠的Blink樹采用一種比較粗暴的方式(也許它認為删除操作的執行次數相對較少:D)。當發生删除操作時,它采用index粒度的X鎖,堵塞其它讀/寫操作,避免了dangling pointer錯誤的發生。
/* Algorithm8. 寫操作 */
1. current <= root
2. While current is not leaf do {
3. current <= scannode(current, v)
4. stack <= current
5. current <= current->son
6. }
7. XL(current) /* lock the current leaf */
8. moveRight(current)
9. DoInsertion:
10. If current is safe do
11. insert(current) and XU(current)
12. else {
13. allocate(next)
14. shift(next) + link(next)
15. modify(current)
16. oldnode <= current
17. current <= pop(stack)
18. XL(current)
19. moveRight(current)
20. XU(oldnode)
21. goto DoInsertion;
22. }
雖然Blink樹的寫操作相對複雜一些,但是對讀操作的原理有了一定的了解後,寫操作了解起來也不再那麼複雜。寫操作使用和讀操作類似的方式定位到目标葉節點
current
并加鎖(
step1-8
)。為了支援自底向上加鎖,寫操作周遊過程中将通路到的樹節點壓入棧
stack
中。如果葉節點是安全節點,直接插入後釋放鎖就可以了(
step10-11
)。如果葉節點不是安全節點,就配置設定一個新的
next
節點,将葉節點的資料移動到
next
節點,修改
current
節點并将右指針指向
next
節點(
step13-15
)。然後,寫操作從棧中彈出上一層的父節點并加鎖(
step16-18
)。由于父節點也可能被分裂,是以也需要通過
moveRight
函數移動到正确的上一層節點(
step19
),然後重複上述的
DoInsertion
過程。
moveRight
scanNode
相似,主要的差別在于前者是在加鎖狀态下向右走,拿到右節點的鎖後可釋放目前結點的鎖。寫操作通過樹節點粒度的鎖,避免了多個寫操作同時修改同一個樹節點,滿足W.1的正确性要求。
對于死鎖,由于Blink樹隻支援“自左向右,自底向上”加鎖的政策,是以不會出現死鎖的問題。
OLFIT樹,版本号你值得擁有
雖然Blink樹有效減少了加鎖頻率,但是它依然存在兩個問題:1. 不實際的假設:讀寫樹節點的操作是原子性的;2. 删除操作竟然需要鎖住整個索引結構,效率太差了。針對這些問題,還是2001年VLDB上的這篇文章
《Cache-Conscious Concurrency Control of Main-Memory Indexes on Shared-Memory Multiprocessor Systems》
,它提出了
OLFIT樹
,在Blink樹基礎上引入了版本号的概念。
/* Algorithm9. 樹節點的寫操作 */
1. XL(current)
2. Update the node content
3. INCREASE(version)
4. XU(current)
/* Algorithm10. 樹節點的讀操作 */
1. RECORD(version)
2. Read the node content
3. If node is lock, go to step1
4. If version differs, go to step1
Algorithm 9-10
顯示版本号相關的具體操作。
Algorithm 9
顯示寫操作在每個樹節點上的執行過程:它首先鎖住這個節點(
step1
),接着更新這個節點的内容(
step2
),然後遞增樹節點的版本号(
step3
),最後釋放這個節點的鎖(
step4
)。因為讀操作在讀取某個樹節點時樹節點可能被修改/分裂/删除,寫操作通過鎖告知讀操作這個樹節點正在被修改,通過版本号告知讀操作這個樹節點已經被修改。
Algorithm 10
顯示讀操作在每個樹結點上的執行過程:它首先記錄這個樹節點的版本号(
step1
),再讀取這個樹節點的内容(
step2
),在讀操作結束後再次讀取節點的鎖和版本号。如果節點的鎖或者版本号發生變化,它判斷自己讀取的樹節點可能處于不一緻的中間狀态,是以從(
step1
)重新開始執行。
/* Algorithm11. OLFIT樹的讀操作 */
1. current <= root
2. While current is not leaf do {
3. RECORD(version)
4. next <= scanNode(current, v)
5. If version/lock is not modified do
6. current <= next
7. }
8. /* Keep move right if necessary. */
9. /* Deal with the leaf node. */
Algorithm 11
顯示了讀操作的完整過程。(
step1-7
)的過程與Blink樹相似,差別在于OLFIT樹在通路每個節點時根據版本号/鎖的狀态判斷自己是否讀到正确的資料,進而避免讀到修改到一半的樹節點,滿足R.1的正确性要求。對于删除操作,為了避免讀操作正在通路的節點被其它寫操作删除,OLFIT樹可以采用
epoch-based reclamation
機制[7]。原理簡單來說就是将删除操作分為邏輯删除和實體删除兩個步驟,隻有在確定一個樹節點沒有被任何操作通路時才可以回收這個樹節點的實體空間。筆者曾完整實作epoch-based garbage collector,但由于篇幅和時間所限,有機會在以後的月報中再詳細分析,本文對此不做贅述。感興趣的讀者可以參考引用[7]這篇文章。
此外,除了版本号操作以外,OLFIT樹的寫操作與Blink樹相似,是以将寫操作的僞代碼留給讀者自己思考。另外,OLFIT樹的加鎖順序與Blink樹一樣,是以不存在死鎖問題。
Masstree,B+樹優化機制的集大成者
系統領域頂級會議
EuroSys
在2012年發表一篇文章:
《Cache craftiness for fast multicore key-value storage》
,提出了
Masstree
。Masstree融合了大量B+樹的優化政策,包括單線程場景下和多線程場景下的。本文簡單介紹一下Masstree采用的幾個主要優化政策,具體情況可參照原論文。
在單線程場景下:
- 采用了B+樹 + Tri樹的混合資料結構。在傳統B+樹中,為了支援變長鍵值這一場景,B+樹要麼在樹節點中預留很大的鍵值空間,然而這會導緻存儲空間的浪費。還有一種方式就是B+樹采用定長指針指向變長鍵值,這節約了存儲空間,負面效果就是存在大量指針通路,可能導緻處理器緩存命中率的嚴重降低,影響索引結構的性能。為了解決這一問題,Masstree提出B+樹 + Tri樹的混合資料結構,将變長鍵值分為多個固長的部分,固長部分通過B+樹組織,多個固長部分間的關系通過Tri樹組織,取得了在空間使用率+性能兩者間的平衡。
- 基于int類型的比較。Masstree将變長鍵值劃分成多個固長部分,每個固長部分可以通過int類型表示,而不是char類型。由于處理器處理int類型比較操作的速度遠遠快于char數組的比較,是以Masstree通過int類型的比較進一步加速了查找過程。
- 預取指令。對于B+樹從根節點到葉節點的周遊操作,絕大部分延遲是訪存延遲(對于基于外存的B+樹,則是外存延遲)造成的,是以Masstree通過預取指令減少訪存延遲。
在多線程場景下:
- 雙向連結清單:之前的OLFIT樹論文并沒有很清楚地說明并發删除操作的實作,Masstree通過維護雙向連結清單,可以在樹節點粒度的鎖基礎上實作并發删除操作。
- 消除不必要的版本号變化,減少重做開銷:在OLFIT樹中,任何一個樹節點的操作都會導緻樹節點的版本号發生變化,這會導緻同時通路該節點的讀操作重做。然而,有一部分樹節點的寫操作并不會導緻讀操作讀到一個錯誤的狀态,是以不需要改變版本号。例如,對于更新操作,在8B範圍内的更新操作是原子性的,讀操作不會讀到一個錯誤的狀态;超過8B範圍的更新操作也可以做成原子性的,即用指針指向超過8B範圍的資料,更新操作隻需要修改8B的指針就可以了;對于插入操作,傳統B+樹的插入操作往往會導緻鍵值對的重排序,這需要通過版本号的變化通知讀操作可能讀到不一緻的狀态。而在Masstree中,它通過8B的permutation維護樹節點鍵值對的有序性,避免傳統B+樹中鍵值對排序的操作,但是每個樹節點最多隻能容納15個鍵值對。
在分析完B+樹并發控制機制幾十年的發展後,本文重新審視MySQL中B+樹并發控制機制的現狀。從MySQL5.6版本更新到5.7版本的過程中,B+樹的并發機制發生了比較大的變化,主要包括以下幾點:(1)引入了SX鎖;(2)寫操作盡可能隻鎖住修改分支,減少加鎖的範圍。具體僞代碼如下:
/* Algorithm12. 讀操作 */
1. SL(index)
2. While current is not leaf do {
3. SL(non-leaf)
4. }
5. SL(leaf)
6. SU(non-leaf)
7. SU(index)
8. Read the leaf node
9. SU(leaf)
Algorithm 12
中,每個讀操作首先對樹結構加S鎖(
step1
step2-4
)。這裡與5.6不同之處在于,讀操作對經過的所有葉節點加S鎖。接着,它對葉節點的page加S鎖(
step5
)後釋放了索引結構和非葉節點的S鎖(
step6-7
)。最後,它通路葉節點的内容(
step8
),釋放了葉節點的鎖(
step9
)。顯而易見,讀操作能滿足R.1/R.2的正确性要求。
/* Algorithm13. 樂觀寫操作 */
1. SL(index)
2. While current is not leaf do {
3. SL(non-leaf)
4. }
5. XL(leaf)
6. SU(non-leaf)
7. SU(index)
8. Modify the leaf node
9. XU(leaf)
Algorithm 13
中的樂觀寫操作與
Algorithm 12
十分相似,主要的差別在于寫操作對葉節點加X鎖。
/* Algorithm14. 悲觀寫操作 */
1. SX(index)
2. While current is not leaf do {
3. XL(modified non-leaf)
4. }
5. XL(leaf) /* lock prev/curr/next leaf */
6. Modify the tree structure
7. XU(non-leaf)
8. SXU(index)
9. Modify the leaf node
10. XU(leaf)
Algorithm 14
中,寫操作首先對樹結構加SX鎖(
step1
),在周遊樹結構的過程中對被影響的分支加X鎖(
step2-4
),對葉節點加X鎖(
step5
),然後修改樹結構後釋放非葉節點和索引的鎖(
step6-8
),最後修改葉節點并釋放鎖(
step9-10
)。寫操作和無死鎖的正确性與前文相似,不做贅述。相比于MySQL5.6,5.7中的悲觀寫操作不會再鎖住整個樹結構,而是鎖住被修改的分支,進而沒有沖突的讀操作可以并發執行,減少了線程之間的沖突。
然而,将之前幾種B+樹并發控制機制與MySQL5.7相比,讀者不免會有幾個疑惑:
- [1] 為什麼在頁鎖的基礎上還需要索引鎖?
- [2] 為什麼讀/樂觀寫操作在持有索引鎖後,還需要一直對非葉節點加鎖?
- [3] MySQL是否可以像Masstree/OLFIT樹/Blink樹一樣,自底向上加鎖,減少加鎖開銷?如果可以,又有多大的收益?
MySQL中的索引結構已經不再是一棵普通的B+樹,它需要支援spatial index這樣更加複雜的索引結構,需要在history list過大的時候優先支援purging線程,存在需要鎖住左-目前節點-右節點這樣的情況,是以它依賴索引的S/SX/X鎖來避免有兩個寫操作同時修改樹結構。此外,它還需要支援類似modify_prev/search_prev等相對複雜的回溯操作,是以需要對非葉節點加鎖,避免被其它操作所修改。并且,一個執行個體可能存在多個聚集索引和二級索引,MySQL中B+樹考慮的情況變得十分複雜。如何在現有MySQL基礎上提高索引結構的多線程擴充性,請持續關注阿裡雲資料庫核心組後續的工作。
索引結構作為影響資料庫系統性能的關鍵子產品,對資料庫系統在高并發場景下的性能表現具有重大影響。本文以B+樹并發機制的幾個代表性工作為例,深入分析了并發機制的發展和現有系統中可能存在的改進空間,希望大家看完以後有一定的收獲。随着多線程索引結構的不斷研究,學界已經出現了幾種Lock-Free B+樹的設計,其中有幾種設計受到了工業界的廣泛關注,甚至已經使用到真實産品中。由于本文篇幅所限,在後續的月報中,我們還會詳細分析以Bw-Tree為代表的Lock-Free B+樹,并且剖析其它類型索引結構的原理和發展(例如LSM-Tree,SkipList,Hash等等),請持續關注阿裡雲資料庫核心團隊!!!
為了高并發場景下更加優異的性能,POLARDB一直在努力,歡迎使用POLARDB!!!歡迎加入POLARDB!!!
引用
- [1] Bayer R, Mccreight E. Organization and maintenance of large ordered indices[C]// ACM Sigfidet. ACM, 1970:107-141.
- [2] Samadi B. B-trees in a system with multiple users [J]. Information Processing Letters, 1976, 5(4):107-112.
- [3] Bayer R, Schkolnick M. Concurrency of operations on B -trees[J]. Acta Informatica, 1977, 9(1):1-21.
- [4] Lehman P L, Yao S B. Efficient locking for concurrent operations on B-trees[J]. Acm Transactions on Database Systems, 1981, 6(4):650-670.
- [5] Memory Latencies on Intel® Xeon® Processor E5-4600 and E7-4800 product families https://software.intel.com/en-us/blogs/2014/01/28/memory-latencies-on-intel-xeon-processor-e5-4600-and-e7-4800-product-families
- [6] Cha S K, Hwang S, Kim K, et al. Cache-Conscious Concurrency Control of Main-Memory Indexes on Shared-Memory Multiprocessor Systems[J]. Proc of Vldb, 2001:181–190.
- [7] K. Fraser. Practical lock-freedom. Technical Report UCAM- CL-TR-579, University of Cambridge Computer Laboratory, 2004.
- [8] Mao Y, Kohler E, Morris R T. Cache craftiness for fast multicore key-value storage[C]// ACM European Conference on Computer Systems. ACM, 2012:183-196.