在上一篇文章中,我們讨論了單變量和多變量線性回歸的Python實作方法。現在我們講邏輯回歸。大家要注意,如何克服過度拟合的問題,這将是讨論的重點。
基礎知識強烈建議你先看第3周的視訊
講座,首先應該對Python系統有個基本的了解。在這裡,我們将研究一個在業界最廣泛應用的機器學習算法。
邏輯回歸在這部分練習中,你将建立一個邏輯回歸模型來預測一個學生是否能被大學錄取。
場景描述:
假設你是一個大學某系的招生負責人,想根據兩門考試的成績來确定每個申請者的錄取機率。你有以前的曆史資料,可以用它作為邏輯回歸的訓練資料集。對于每一個訓練的例子,你有申請人兩門考試的分數和相應的錄取決策。你的工作是建立一個分類模型,然後根據這兩門考試的成績來預測申請者的錄取機率。
首先要加載必需的庫:
importnumpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt # more on this later
下一步,讀入資料 (在
第3周裡找到)
data = pd.read_csv('ex2data1.txt', header = None)
X = data.iloc[:,:-1]
y = data.iloc[:,2]
data.head()
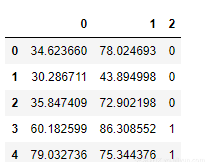
是以,我們有兩個獨立的特征和一個因變量。這裡的“0”表示申請人不能被錄取,而“1”則表示能被錄取。
資料可視化在開始執行任何學習算法之前,如果可能的話,最好一直進行資料的可視化工作。
mask = y == 1
adm = plt.scatter(X[mask][0].values, X[mask][1].values)
not_adm = plt.scatter(X[~mask][0].values, X[~mask][1].values)
plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')
plt.legend((adm, not_adm), ('Admitted', 'Not admitted'))
plt.show()
在開始調用實際成本函數之前,請回想一下,邏輯回歸的假設是利用了S形函數。讓我們首先定義S形函數:
S型函數def sigmoid(x):
return 1/(1+np.exp(-x))
請注意,我們在這裡寫的是向量化的代碼。是以,x是個标量,也是個向量,還是個張量,其實并不重要。當然,編寫和了解向量化的代碼需要花費一些心思。不過,在去掉了循環部分之後,這會使代碼更加的高效和通用。
成本函數以下是我們實作邏輯回歸成本函數的代碼:
defcostFunction(theta, X, y):
J = (-1/m) * np.sum(np.multiply(y, np.log(sigmoid(X @ theta)))
+ np.multiply((1-y), np.log(1 - sigmoid(X @ theta))))
return J
請注意,我們在上面的成本函數中使用了S形函數。
有多種程式設計方法來實作成本函數,不過更重要的是底層的數學思想,還有我們把它轉化成代碼的能力。
梯度函數def gradient(theta, X, y):
return ((1/m) * X.T @ (sigmoid(X @ theta) - y))
我們一定要注意,雖然這個梯度看起來與線性回歸的梯度相同,然而實際上公式是不一樣的,因為線性回歸和邏輯回歸有不同的假設函數定義。
以下是通過初始的參數來進行函數調用的代碼。
(m, n) = X.shape
X = np.hstack((np.ones((m,1)), X))
y = y[:, np.newaxis]
theta = np.zeros((n+1,1)) # intializing theta with all zeros
J = costFunction(theta, X, y)
print(J)
上面的代碼運作之後,會給我們J的輸出值是0.693。
使用 fmin_tnc 來學習參數在前面的任務中,我們通過執行梯度下降的算法來找到線性回歸模型的最優參數,然後寫了一個成本函數,并且計算了它的梯度,最後執行了梯度下降的操作步驟。這一次,我們不執行梯度下降步驟,而是從scipy庫中調用了一個内置的函數fmin_tnc。
fmin_tnc是一個尋找非限制函數的最小值的優化求解函數。對于邏輯回歸,你希望用參數theta來優化成本函數。優化中的限制經常是指對參數的限制。例如, theta可能取值的限制範圍theta≤ 1。然而邏輯回歸就沒有這樣的限制,因為theta是允許采取任何實際值的。
具體來說,在給定固定的資料集(X和y的值)的情況下,你将使用fmin_tnc來找到邏輯回歸的成本函數的最佳或者最優的參數theta。将把以下的輸入傳遞給fmin_tnc:
· 我們想要優化的參數初始值;
· 當給定訓練集和特定theta值時,用來給資料集(X,y)計算theta值的邏輯回歸成本和梯度的函數。
temp = opt.fmin_tnc(func = costFunction,
x0 = theta.flatten(),fprime = gradient,
args = (X, y.flatten()))
#the output of above function is a tuple whose first element #contains the optimized values of theta
theta_optimized = temp[0]
print(theta_optimized)
關于函數
flatten()的注解:
不幸的是,SciPy的sfmin_tnc不能很好地使用行向量或者列向量,它期望的參數是數組形式的。flatten()函數将行向量或者列向量縮小到數組形式。
上面代碼的運作結果應該是[-25.16131862, 0.20623159, 0.20147149]。
如果你正确地執行了costFunction函數,fmin_tnc将在正确的優化參數上進行收斂,并傳回最終的theta值。值得注意的是,通過使用fmin_tnc,你不必自己編寫任何循環程式,也不必像梯度下降那樣設定一個學習率。這都是由fmin_tnc來完成的,你隻需要提供一個函數來計算成本和梯度。
讓我們使用這些優化了的theta值來計算成本。
J = costFunction(theta_optimized[:,np.newaxis], X, y)
你會看到上面代碼運作之後的輸出值是0.203,這可以與使用初始的theta值獲得的成本值0.693對比一下。
繪制決策邊界然後,這個最終的theta值将被用來繪制訓練資料的決策邊界,進而會得到一個類似于下面的圖。
plot_x = [np.min(X[:,1]-2), np.max(X[:,2]+2)]
plot_y = -1/theta_optimized[2]*(theta_optimized[0]
+ np.dot(theta_optimized[1],plot_x))
mask = y.flatten() == 1
adm = plt.scatter(X[mask][:,1], X[mask][:,2])
not_adm = plt.scatter(X[~mask][:,1], X[~mask][:,2])
decision_boun = plt.plot(plot_x, plot_y)
通過上面的結果,看起來我們的模型在區分那些被錄取的和沒有被錄取的學生的方面做得非常好。接下來要量化模型的精度,我們将為這個模型編寫一個稱為accuracy的函數。
def accuracy(X, y, theta, cutoff):
pred = [sigmoid(np.dot(X, theta)) >= cutoff]
acc = np.mean(pred == y)
print(acc * 100)
accuracy(X, y.flatten(), theta_ans[0], 0.5)
運作之後,應該會輸出一個結果為89%的精度值。
本文由北郵
@愛可可-愛生活老師推薦,
阿裡雲雲栖社群組織翻譯。
文章原标題《Python Implementation of Andrew Ng’s Machine Learning Course (Part 2.1)》
作者:Srikar
譯者:奧特曼,審校:袁虎。
文章為簡譯,更為詳細的内容,請檢視
原文