單源最短路徑問題是指,給定一個圖G=(V,E),希望找到從給定源結點s到每個節點v的最短路徑。單源最短路徑問題可以用來解決很多最短路徑的變體。
單目的地最短路徑問題:找到從每個結點v到給定目的地結點t的最短路徑。将圖的每條邊翻轉,這個問題可以轉換為單源最短路徑問題。
單結點對最短路徑問題:找到從給定結點u到給定結點v的最短路徑。如果已經解決了u的單元最短路徑問題,則該問題已經解決。
在單源最短路徑問題中,根據圖的性質不同有不同的解決方案。主要的性質有:是有向圖還是無向圖,是權重圖還是機關圖,有無負權重的邊,是否有環。
Dijkstra算法
Dijkstra算法解決的是非負權重有向圖上的單源最短路徑問題。算法邏輯為維持一個結點集合S,集合中每個結點之間的最短路徑已經被找到,重複從集合V-S中選擇與源結點r之間最短路徑估計最小的結點u加入到S,然後對所有從u出發的邊檢查r到u的距離加上該邊的距離是否小于該邊另一個結點原本的最短路徑估計。
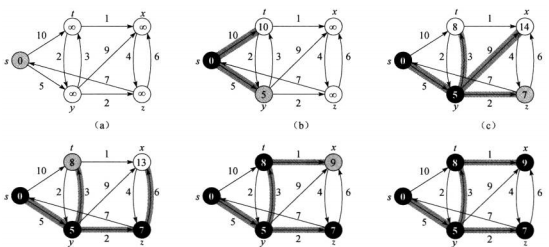
如圖(a)初始狀态,s是源結點,加入到集合S中
(b)檢查s出發的路徑(s,t)和(s,y)更新y和t的最短路徑估計
(c)在剩下結點中選擇最短路徑估計最小的結點y,然後檢查從y出發的路徑(y,t)+(s,y)=8<10,更新t的距離為8,同樣對x和z也進行同樣的操作,結束後y加入到S中
(d)接下來選擇z結點,(z,s)+7=14>s,是以s保持不變,而(z,x)+6=13<14,x的值更新為13,然後将z加入到S中。
(e)-(f)的操作同上,不再做較長的描述。最終所有點都加入到了S中。
為了完成算法,我們需要存儲每個結點的最短路徑估計和他們的前驅結點來輸出最終路徑,同時需要一個最小優先隊列來儲存V-S中結點的最短路徑估計排序,否則需要周遊V-S中的結點來選擇出最短的那個。直接周遊所有邊的算法複雜度為O(V^2),若使用最小二叉堆來存儲優先隊列則複雜度可以降低為O((V+E)lgV)。
1 #include<stdio.h>
2 using namespace std;
3 #define SIZE 10
4 #define INFI 10000
5
6 int G[SIZE][SIZE];//鄰接矩陣,參數初始化略
7 int dist[SIZE];//與根間的距離估計
8 bool visit[SIZE];//是否被通路過
9
10 void dijkstra(int root){
11 int i,j;
12 int min;
13 for(i = 0; i < SIZE; i++){
14 dist[i] = INFI;
15 visit[i] = false;
16 }
17 dist[root] = 0;
18 for(i = 0; i <SIZE; i++){
19 min = 0;//尋找剩餘點中距離根最近的點
20 for(j = 1; j < SIZE;j++){
21 if(!visit[j] && dist[j] < dist[min]){
22 min = j;
23 }
24 }
25 for(j = 0; j < SIZE; j++){
26 if(!visit[j] && G[min][j] + dist[min] < dist[j])
27 dist[j] = G[min][j] + dist[min];//檢查是否需要更新最短路徑
28 }
29 visit[min] = true;
30 }
31 } Bellman-Ford算法
該算法可以解決負權重邊的圖,算法傳回一個布爾值,表明是否存在一個從源節點可以到達的權重為負的環路,若存在則算法将告訴我們不存在解決方案,因為這個環路的存在會導緻出現距離為負無窮的點。
算法需要進行|V|-1次循環,每次循環按照同樣的順序對所有邊進行松弛,結束後檢查是否存在權重為負的環路。算法複雜度為O(VE),是以該算法在處理密集圖時效率會降低,總體效率不如dijkstra算法。
如圖所示每一次松弛邊的順序都是(t,x) (t,y) (t,z) (y,x) (y,z) (z,x) (z,s) (s,t) (s,y)。源結點為s,加了陰影的邊表示前驅路徑。
(a) 更新源結點的距離為0
(b) 按照順序,僅(s,t) (s,y)可以更新結點的值,t=6 y=7
(c) (t,z) (y,x)可以更新z和x的值
(d) (x,t)可以更新t的值
(e) 本次循環沒有可以更新的值,檢查不存在權值為負的環傳回TRUE
1 #include<stdio.h>
2 using namespace std;
3 #define SIZE 10
4 #define INFI 10000
5
6 int G[SIZE][SIZE];//鄰接矩陣,參數初始化略
7 int dist[SIZE];//與根間的距離估計
8 int p[SIZE];//前驅結點
9
10 void bellmanFord(int root){
11 int i, j, k;
12 for(i = 0; i < SIZE; i++){
13 dist[i] = INFI;
14 }
15 dist[root] = 0;
16 for(i = 0; i < SIZE - 1; i++){
17 for(j = 0; j < SIZE; j++){
18 if(dist[j] == INFI)
19 continue;//結點無法從源結點到達則先跳過
20 for(k = 0; k < SIZE; k++){
21 if(G[j][k] != 0 && G[j][k] + dist[j] < dist[k])
22 dist[k] = G[j][k] + dist[j];//松弛路徑
23 }
24 }
25 }
26 for(i = 0; i < SIZE; i++){
27 for(j = 0; j < SIZE; j++){
28 if(G[i][j] != 0 && dist[i] > dist[j] + G[i][j])
29 return false;//檢查有無權重為負的環
30 }
31 }
32 } 差分限制和最短路徑
線上性規劃問題中,通常會給定一個m*n的矩陣A、一個m維的向量b和一個n維向量c,希望找到一個n維向量x,使得在有Ax≤b給定的m個限制條件下優化目标函數
,
使目标函數值最大。在一個差分限制系統中,線性規劃矩陣A的每一個行包括一個1和一個-1,其他所有項都是0,每個限制條件變為不等式xj-xi≤bk。
如圖所示的矩陣和向量可以表示為8個簡單不等式,要求出一組可行解。以x作為結點,後面的限制值作為路徑權重,可以畫出一張限制圖
可以通過對限制圖設定一個源結點,如v0求出最短路徑解來獲得一組可行解。因為含有負值權重,是以需要通過Bellman-Ford算法來進行求解。
個人GitHub位址: https://github.com/GrayWind33