1. 挖掘關聯規則
1.1 什麼是關聯規則
一言蔽之,關聯規則是形如X→Y的蘊涵式,表示通過X可以推導“得到”Y,其中X和Y分别稱為關聯規則的先導(antecedent或left-hand-side, LHS)和後繼(consequent或right-hand-side, RHS)
1.2 如何量化關聯規則
關聯規則挖掘的一個典型例子便是購物車分析。通過關聯規則挖掘能夠發現顧客放入購物車中的不同商品之間的關聯,分析顧客的消費習慣。這種關聯規則的方向能夠幫助賣家了解哪些商品被顧客頻繁購買,進而幫助他們開發更好的營銷政策。比如:将經常同時購買的商品擺近一些,以便進一步刺激這些商品一起銷售;或者,将兩件經常同時購買的商品擺遠一點,這樣可能誘發買這兩件商品的使用者一路挑選其他商品。
在資料挖掘當中,通常用“支援度”(support)和“置性度”(confidence)兩個概念來量化事物之間的關聯規則。它們分别反映所發現規則的有用性和确定性。比如:
Computer => antivirus_software , 其中 support=2%, confidence=60%
表示的意思是所有的商品交易中有2%的顧客同時買了電腦和防毒軟體,并且購買電腦的顧客中有60%也購買了防毒軟體。在關聯規則的挖掘過程中,通常會設定最小支援度門檻值和最小置性度門檻值,如果某條關聯規則滿足最小支援度門檻值和最小置性度門檻值,則認為該規則可以給使用者帶來感興趣的資訊。
1.3 關聯規則挖掘過程
1)幾個基本概念:
關聯規則A->B的支援度support=P(AB),指的是事件A和事件B同時發生的機率。
置信度confidence=P(B|A)=P(AB)/P(A),指的是發生事件A的基礎上發生事件B的機率。
同時滿足最小支援度門檻值和最小置信度門檻值的規則稱為強規則。
如果事件A中包含k個元素,那麼稱這個事件A為k項集,并且事件A滿足最小支援度門檻值的事件稱為頻繁k項集。
2)挖掘過程:
第一,找出所有的頻繁項集;
第二,由頻繁項集産生強規則。
2. 什麼是Apriori
2.1 Apriori介紹
Apriori算法使用頻繁項集的先驗知識,使用一種稱作逐層搜尋的疊代方法,k項集用于探索(k+1)項集。首先,通過掃描事務(交易)記錄,找出所有的頻繁1項集,該集合記做L1,然後利用L1找頻繁2項集的集合L2,L2找L3,如此下去,直到不能再找到任何頻繁k項集。最後再在所有的頻繁集中找出強規則,即産生使用者感興趣的關聯規則。
其中,Apriori算法具有這樣一條性質:任一頻繁項集的所有非空子集也必須是頻繁的。因為假如P(I)< 最小支援度門檻值,當有元素A添加到I中時,結果項集(A∩I)不可能比I出現次數更多。是以A∩I也不是頻繁的。
2.2 連接配接步和剪枝步
在上述的關聯規則挖掘過程的兩個步驟中,第一步往往是總體性能的瓶頸。Apriori算法采用連接配接步和剪枝步兩種方式來找出所有的頻繁項集。
1) 連接配接步
為找出Lk(所有的頻繁k項集的集合),通過将Lk-1(所有的頻繁k-1項集的集合)與自身連接配接産生候選k項集的集合。候選集合記作Ck。設l1和l2是Lk-1中的成員。記li[j]表示li中的第j項。假設Apriori算法對事務或項集中的項按字典次序排序,即對于(k-1)項集li,li[1]<li[2]<……….<li[k-1]。将Lk-1與自身連接配接,如果(l1[1]=l2[1])&&( l1[2]=l2[2])&&……..&& (l1[k-2]=l2[k-2])&&(l1[k-1]<l2[k-1]),那認為l1和l2是可連接配接。連接配接l1和l2 産生的結果是{l1[1],l1[2],……,l1[k-1],l2[k-1]}。
2) 剪枝步
CK是LK的超集,也就是說,CK的成員可能是也可能不是頻繁的。通過掃描所有的事務(交易),确定CK中每個候選的計數,判斷是否小于最小支援度計數,如果不是,則認為該候選是頻繁的。為了壓縮Ck,可以利用Apriori性質:任一頻繁項集的所有非空子集也必須是頻繁的,反之,如果某個候選的非空子集不是頻繁的,那麼該候選肯定不是頻繁的,進而可以将其從CK中删除。
(Tip:為什麼要壓縮CK呢?因為實際情況下事務記錄往往是儲存在外存儲上,比如資料庫或者其他格式的檔案上,在每次計算候選計數時都需要将候選與所有事務進行比對,衆所周知,通路外存的效率往往都比較低,是以Apriori加入了所謂的剪枝步,事先對候選集進行過濾,以減少通路外存的次數。)
2.3 Apriori算法執行個體
| 交易ID | 商品ID清單 |
| T100 | I1,I2,I5 |
| T200 | I2,I4 |
| T300 | I2,I3 |
| T400 | I1,I2,I4 |
| T500 | I1,I3 |
| T600 | |
| T700 | |
| T800 | I1,I2,I3,I5 |
| T900 | I1,I2,I3 |
上圖為某商場的交易記錄,共有9個事務,利用Apriori算法尋找所有的頻繁項集的過程如下:
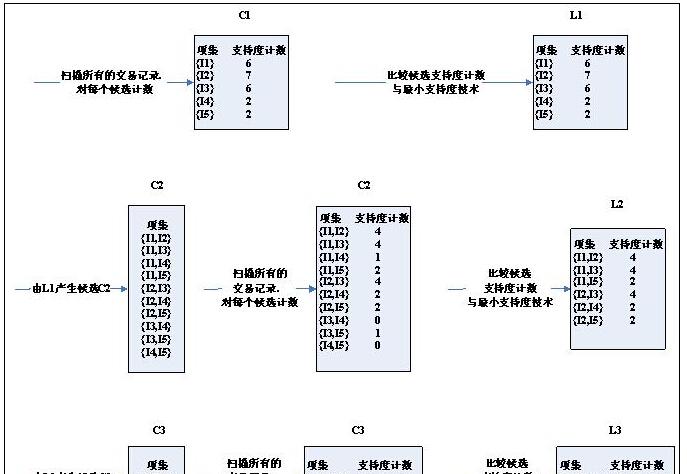
詳細介紹下候選3項集的集合C3的産生過程:從連接配接步,首先C3={{I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}}(C3是由L2與自身連接配接産生)。根據Apriori性質,頻繁項集的所有子集也必須頻繁的,可以确定有4個候選集{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}}不可能時頻繁的,因為它們存在子集不屬于頻繁集,是以将它們從C3中删除。注意,由于Apriori算法使用逐層搜尋技術,給定候選k項集後,隻需檢查它們的(k-1)個子集是否頻繁。
3. Apriori僞代碼
| 算法:Apriori 輸入:D - 事務資料庫;min_sup - 最小支援度計數門檻值 輸出:L - D中的頻繁項集 方法: L1=find_frequent_1-itemsets(D); // 找出所有頻繁1項集 For(k=2;Lk-1!=null;k++){ Ck=apriori_gen(Lk-1); // 産生候選,并剪枝 For each 事務t in D{ // 掃描D進行候選計數 Ct =subset(Ck,t); // 得到t的子集 For each 候選c 屬于 Ct c.count++; } Lk={c屬于Ck | c.count>=min_sup} } Return L=所有的頻繁集; Procedure apriori_gen(Lk-1:frequent(k-1)-itemsets) For each項集l1屬于Lk-1 For each項集 l2屬于Lk-1 If((l1[1]=l2[1])&&( l1[2]=l2[2])&&…….. && (l1[k-2]=l2[k-2])&&(l1[k-1]<l2[k-1])) then{ c=l1連接配接l2 //連接配接步:産生候選 if has_infrequent_subset(c,Lk-1) then delete c; //剪枝步:删除非頻繁候選 else add c to Ck; } Return Ck; Procedure has_infrequent_sub(c:candidate k-itemset; Lk-1:frequent(k-1)-itemsets) For each(k-1)-subset s of c If s不屬于Lk-1 then Return true; Return false; |
4. 由頻繁項集産生關聯規則
Confidence(A->B)=P(B|A)=support_count(AB)/support_count(A)
關聯規則産生步驟如下:
1) 對于每個頻繁項集l,産生其所有非空真子集;
2) 對于每個非空真子集s,如果support_count(l)/support_count(s)>=min_conf,則輸出 s->(l-s),其中,min_conf是最小置信度門檻值。
例如,在上述例子中,針對頻繁集{I1,I2,I5}。可以産生哪些關聯規則?該頻繁集的非空真子集有{I1,I2},{I1,I5},{I2,I5},{I1 },{I2}和{I5},對應置信度如下:
I1&&I2->I5 confidence=2/4=50%
I1&&I5->I2 confidence=2/2=100%
I2&&I5->I1 confidence=2/2=100%
I1 ->I2&&I5 confidence=2/6=33%
I2 ->I1&&I5 confidence=2/7=29%
I5 ->I1&&I2 confidence=2/2=100%
如果min_conf=70%,則強規則有I1&&I5->I2,I2&&I5->I1,I5 ->I1&&I2。
5. Apriori Java代碼
package com.apriori;
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Set;
public class Apriori {
private final static int SUPPORT = 2; // 支援度門檻值
private final static double CONFIDENCE = 0.7; // 置信度門檻值
private final static String ITEM_SPLIT=";"; // 項之間的分隔符
private final static String CON="->"; // 項之間的分隔符
private final static List<String> transList=new ArrayList<String>(); //所有交易
static{//初始化交易記錄
transList.add("1;2;5;");
transList.add("2;4;");
transList.add("2;3;");
transList.add("1;2;4;");
transList.add("1;3;");
transList.add("1;2;3;5;");
transList.add("1;2;3;");
}
public Map<String,Integer> getFC(){
Map<String,Integer> frequentCollectionMap=new HashMap<String,Integer>();//所有的頻繁集
frequentCollectionMap.putAll(getItem1FC());
Map<String,Integer> itemkFcMap=new HashMap<String,Integer>();
itemkFcMap.putAll(getItem1FC());
while(itemkFcMap!=null&&itemkFcMap.size()!=0){
Map<String,Integer> candidateCollection=getCandidateCollection(itemkFcMap);
Set<String> ccKeySet=candidateCollection.keySet();
//對候選集項進行累加計數
for(String trans:transList){
for(String candidate:ccKeySet){
boolean flag=true;// 用來判斷交易中是否出現該候選項,如果出現,計數加1
String[] candidateItems=candidate.split(ITEM_SPLIT);
for(String candidateItem:candidateItems){
if(trans.indexOf(candidateItem+ITEM_SPLIT)==-1){
flag=false;
break;
}
}
if(flag){
Integer count=candidateCollection.get(candidate);
candidateCollection.put(candidate, count+1);
}
}
//從候選集中找到符合支援度的頻繁集項
itemkFcMap.clear();
for(String candidate:ccKeySet){
Integer count=candidateCollection.get(candidate);
if(count>=SUPPORT){
itemkFcMap.put(candidate, count);
//合并所有頻繁集
frequentCollectionMap.putAll(itemkFcMap);
return frequentCollectionMap;
private Map<String,Integer> getCandidateCollection(Map<String,Integer> itemkFcMap){
Map<String,Integer> candidateCollection=new HashMap<String,Integer>();
Set<String> itemkSet1=itemkFcMap.keySet();
Set<String> itemkSet2=itemkFcMap.keySet();
for(String itemk1:itemkSet1){
for(String itemk2:itemkSet2){
//進行連接配接
String[] tmp1=itemk1.split(ITEM_SPLIT);
String[] tmp2=itemk2.split(ITEM_SPLIT);
String c="";
if(tmp1.length==1){
if(tmp1[0].compareTo(tmp2[0])<0){
c=tmp1[0]+ITEM_SPLIT+tmp2[0]+ITEM_SPLIT;
}
}else{
boolean flag=true;
for(int i=0;i<tmp1.length-1;i++){
if(!tmp1[i].equals(tmp2[i])){
flag=false;
break;
}
}
if(flag&&(tmp1[tmp1.length-1].compareTo(tmp2[tmp2.length-1])<0)){
c=itemk1+tmp2[tmp2.length-1]+ITEM_SPLIT;
}
//進行剪枝
boolean hasInfrequentSubSet = false;
if (!c.equals("")) {
String[] tmpC = c.split(ITEM_SPLIT);
for (int i = 0; i < tmpC.length; i++) {
String subC = "";
for (int j = 0; j < tmpC.length; j++) {
if (i != j) {
subC = subC+tmpC[j]+ITEM_SPLIT;
}
}
if (itemkFcMap.get(subC) == null) {
hasInfrequentSubSet = true;
break;
hasInfrequentSubSet=true;
if(!hasInfrequentSubSet){
candidateCollection.put(c, 0);
}
}
return candidateCollection;
private Map<String,Integer> getItem1FC(){
Map<String,Integer> sItem1FcMap=new HashMap<String,Integer>();
Map<String,Integer> rItem1FcMap=new HashMap<String,Integer>();//頻繁1項集
for(String trans:transList){
String[] items=trans.split(ITEM_SPLIT);
for(String item:items){
Integer count=sItem1FcMap.get(item+ITEM_SPLIT);
if(count==null){
sItem1FcMap.put(item+ITEM_SPLIT, 1);
sItem1FcMap.put(item+ITEM_SPLIT, count+1);
Set<String> keySet=sItem1FcMap.keySet();
for(String key:keySet){
Integer count=sItem1FcMap.get(key);
if(count>=SUPPORT){
rItem1FcMap.put(key, count);
return rItem1FcMap;
public Map<String,Double> getRelationRules(Map<String,Integer> frequentCollectionMap){
Map<String,Double> relationRules=new HashMap<String,Double>();
Set<String> keySet=frequentCollectionMap.keySet();
for (String key : keySet) {
double countAll=frequentCollectionMap.get(key);
String[] keyItems = key.split(ITEM_SPLIT);
if(keyItems.length>1){
List<String> source=new ArrayList<String>();
Collections.addAll(source, keyItems);
List<List<String>> result=new ArrayList<List<String>>();
buildSubSet(source,result);//獲得source的所有非空子集
for(List<String> itemList:result){
if(itemList.size()<source.size()){//隻處理真子集
List<String> otherList=new ArrayList<String>();
for(String sourceItem:source){
if(!itemList.contains(sourceItem)){
otherList.add(sourceItem);
}
String reasonStr="";//前置
String resultStr="";//結果
for(String item:itemList){
reasonStr=reasonStr+item+ITEM_SPLIT;
}
for(String item:otherList){
resultStr=resultStr+item+ITEM_SPLIT;
double countReason=frequentCollectionMap.get(reasonStr);
double itemConfidence=countAll/countReason;//計算置信度
if(itemConfidence>=CONFIDENCE){
String rule=reasonStr+CON+resultStr;
relationRules.put(rule, itemConfidence);
return relationRules;
private void buildSubSet(List<String> sourceSet, List<List<String>> result) {
// 僅有一個元素時,遞歸終止。此時非空子集僅為其自身,是以直接添加到result中
if (sourceSet.size() == 1) {
List<String> set = new ArrayList<String>();
set.add(sourceSet.get(0));
result.add(set);
} else if (sourceSet.size() > 1) {
// 當有n個元素時,遞歸求出前n-1個子集,在于result中
buildSubSet(sourceSet.subList(0, sourceSet.size() - 1), result);
int size = result.size();// 求出此時result的長度,用于後面的追加第n個元素時計數
// 把第n個元素加入到集合中
List<String> single = new ArrayList<String>();
single.add(sourceSet.get(sourceSet.size() - 1));
result.add(single);
// 在保留前面的n-1子集的情況下,把第n個元素分别加到前n個子集中,并把新的集加入到result中;
// 為保留原有n-1的子集,是以需要先對其進行複制
List<String> clone;
for (int i = 0; i < size; i++) {
clone = new ArrayList<String>();
for (String str : result.get(i)) {
clone.add(str);
clone.add(sourceSet.get(sourceSet.size() - 1));
result.add(clone);
public static void main(String[] args){
Apriori apriori=new Apriori();
Map<String,Integer> frequentCollectionMap=apriori.getFC();
System.out.println("----------------頻繁集"+"----------------");
Set<String> fcKeySet=frequentCollectionMap.keySet();
for(String fcKey:fcKeySet){
System.out.println(fcKey+" : "+frequentCollectionMap.get(fcKey));
Map<String,Double> relationRulesMap=apriori.getRelationRules(frequentCollectionMap);
System.out.println("----------------關聯規則"+"----------------");
Set<String> rrKeySet=relationRulesMap.keySet();
for(String rrKey:rrKeySet){
System.out.println(rrKey+" : "+relationRulesMap.get(rrKey));
轉自:http://blog.csdn.net/rongyongfeikai2/article/details/40457827