Abstract
上一節:三角形光栅化
z-buffer 深度緩存技術。
Reference :
- https://github.com/ssloy/tinyrenderer/wiki/Lesson-3-Hidden-faces-removal-(z-buffer)
從一個簡單場景着手
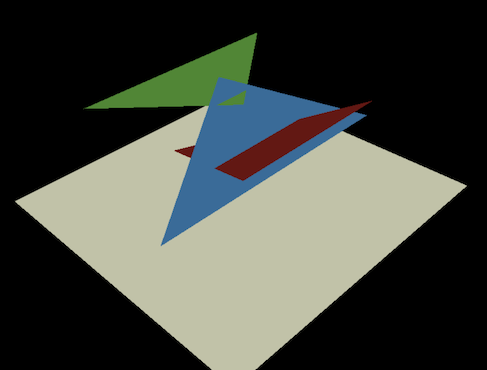
如上圖,米白色的底面為投影螢幕,空中是三個互相交錯的三角形,而相機俯覽地将這些三角形投射到螢幕上:
注意這幾個三角形呈現了一種相對複雜的覆寫關系,若用上章那樣的畫家算法Painter's algorithm将會導緻錯誤的覆寫順序。
暫時丢棄次元 \(z\) ,考慮一下 "Y-buffer"
想象一下,從此場景的側面 --- 平行于投影平面的方向看,場景會變成這個樣子:
現在我們将這幾個三角形看作三條線。"Y-buffer"的原理為,分别繪制紅、綠、藍線,每次從場景左端開始用一條線掃描到右端。若此條線與掃描線 \(x = a\) 交點的 \(y\) 值大于上一次更新過的 ybuffer[a] ,則說明該交點在視覺上對目前掃描線對應的已存在投影點存在覆寫關系,那麼目前投影點應更新為此交點的顔色。
不難想象,所有計算完成後,圖像會是一條與平面同寬,高隻有1的顔色線,因為這是二維投影到一維,不是嗎?但我們但螢幕分辨率都比較高,這樣看起來費眼睛,于是可以将Render的高設為16 pixels來讓觀察更為輕松:
void rasterize(Vec2i p0, Vec2i p1, TGAImage &image, TGAColor color, int ybuffer[]) {
// 修正掃描順序
if (p0.x>p1.x) {
std::swap(p0, p1);
}
for (int x=p0.x; x<=p1.x; x++) {
float t = (x-p0.x)/(float)(p1.x-p0.x);
int y = p0.y*(1.-t) + p1.y*t;
if (ybuffer[x]<y) {
ybuffer[x] = y;
image.set(x, 0, color);
}
}
}
main 函數中,調用前需先将 ybuffer 的深度初始化為 \(-infinity\) ,這樣第一輪掃描就可以産生正确的覆寫關系。
TGAImage render(width, 16, TGAImage::RGB);
int ybuffer[width];
for (int i=0; i<width; i++) {
ybuffer[i] = std::numeric_limits<int>::min();
}
rasterize(Vec2i(20, 34), Vec2i(744, 400), render, red, ybuffer); // 第一輪掃描
rasterize(Vec2i(120, 434), Vec2i(444, 400), render, green, ybuffer); // 第二輪掃描
rasterize(Vec2i(330, 463), Vec2i(594, 200), render, blue, ybuffer); // 第三輪掃描
// 加寬
for (int i=0; i<width; i++) {
for (int j=1; j<16; j++) {
render.set(i, j, render.get(i, 0));
}
}
渲染出來的顔色條與場景中線之間的遮擋關系能清晰的呈現出對應關系:
回到3D世界
了解2D "Y-buffer" 原理後,自然能将結論推廣到3D空間。
先提前明白一些事情。螢幕是2D的是以一般用兩個次元的容器來存放螢幕像素,但是可以用一維容器來存放,隻需自行計算索引:
已知坐标,求像素索引:
int* zbuffer = new int[width*height];
int index = x + y*width;
已知像素索引,求對應二維坐标:
int x = index % width;
int y = index / width;
現在無外乎多了一個次元 \(z\) ,但我們看問題的角度依然不變。
還記得 "Y-buffer" 例子的計算中,直線上點的 \(y\) 值是由線性插值得來的。擴充到3D情形,三角形面片内部點的 \(z\) 值同樣由線性插值得來,隻是這種線性插值又叫做重心坐标。
展現在代碼上便是,重心坐标不僅能判斷點是否在三角形内,還能完成三角形内點資訊的插值:
Vec3f P;
for (P.x=bboxmin.x; P.x<=bboxmax.x; P.x++) {
for (P.y=bboxmin.y; P.y<=bboxmax.y; P.y++) {
Vec3f bc_screen = barycentric(pts, P);
if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) continue;
P.z = 0;
for (int i=0; i<3; i++) P.z += pts[i][2]*bc_screen[i];
if (zbuffer[int(P.x+P.y*width)]<P.z) {
zbuffer[int(P.x+P.y*width)] = P.z;
image.set(P.x, P.y, color);
}
}
}
采用 z-buffer 的結果就是,上一節嘴部的錯誤繪制被修正:
到了這裡,實際上我們已經實作了基于正交投影的3D着色,且光照模型采用的是 Flat Shading平面着色。這種着色技術容易了解,計算複雜度低,但随之而來但便是不算精細的着色效果。
擴充:紋理映射
雖然人臉模型有了合适的光照,正确的頂點遮擋,但是看起來還是太單調了。能給它表面蒙上一層皮膚就好了。
左邊是我們之前渲染的頭部模型的預覽,右邊是其對應的紋理圖檔。直覺上便是将這張圖檔每個坐标一一對應地貼在模型上不是嗎?
還記得之前渲染的基于 Flat Shading 的人臉嗎,白溜溜的,随着光線角度産生明暗變化,因為我們代碼預設所有點的着色顔色為純白色:
triangle(pts, zbuffer, image, TGAColor(intensity*255, intensity*255, intensity*255, 255));
也即,白色根據光照強度的衰減來産生明暗效果。紋理映射的計算其實大同小異,對于每個三角形面片,頂點在紋理圖檔上取得對應顔色,再為面片内部點進行顔色的插值即可。
小障礙:obj檔案
要做到紋理映射,首先要能了解如何解析obj檔案。這裡有個簡單的例子:一個正方體木箱。
用文本編輯器檢視此obj檔案的内容,會發現分為開頭為 v 、vt 、f 的三個資料區域。(我們選取的例子中沒有 vn 開頭的資料,vn 代表頂點的法向量,在我們已知的 Flat Shading 下暫時用不到)
# 8 vertices
v -1.000000 -1.000000 1.000000
v -1.000000 -1.000000 -1.000000
v 1.000000 -1.000000 -1.000000
v 1.000000 -1.000000 1.000000
v -1.000000 1.000000 1.000000
v -1.000000 1.000000 -1.000000
v 1.000000 1.000000 -1.000000
v 1.000000 1.000000 1.000000
# 4 uvs
vt 0.000000 0.000000
vt 1.000000 0.000000
vt 1.000000 1.000000
vt 0.000000 1.000000
# 6 faces
f 5/1 6/2 2/3 1/4
f 6/1 7/2 3/3 2/4
f 7/1 8/2 4/3 3/4
f 8/1 5/2 1/3 4/4
f 1/1 2/2 3/3 4/4
f 8/1 7/2 6/3 5/4
首先,v 開頭的資料自然為木箱模型的八個頂點 \((x, y, z)\),不信你可以數數。
其次,vt 開頭的資料代表紋理的 \(uv\) 坐标,别被它吓倒,我相信你一聽就懂:
- \(uv\) 坐标範圍為 \([0, 1]\)
- \(uv\) 的意義為紋理圖檔的采樣比例。一張紋理圖檔被四個 \(uv\) 點所包圍,圖檔上每個像素的顔色都能用一組 \(uv\) 與圖檔寬高的乘積算出:
最後,f 開頭的向量表示模型的所有面片,每一條表示一個面片,它同時起到映射的功能。
其格式為 \(f = v_1/vt_1,\ \ v_2/vt_2,\ \ v_3/vt_3,\ ...,\ v_n/vt_n\ \ ,n \ge 3\) ;每個分量為一個 v/vt,同時代表面片的一個頂點;n決定了模型如何描述一個面片的邊數。
拿其中一條來舉例:
# 在這裡,易知 n = 4,即該模型定義一個面片為四邊形。
f 8/1 7/2 6/3 5/4
它表達什麼意思呢?該面片的四個頂點分别對應模型的第8、7、6、5個頂點;
而模型的第8、7、6、5個頂點又分别對應第1、2、3、4個 \(uv\) 點,也即:
f1 = v 1.000000 1.000000 1.000000 -> vt 0.000000 0.000000
f2 = v 1.000000 1.000000 -1.000000 -> vt 1.000000 0.000000
f3 = v -1.000000 1.000000 -1.000000 -> vt 1.000000 1.000000
f4 = v -1.000000 1.000000 1.000000 -> vt 0.000000 1.000000
這條映射帶來的效果即為,由對應 \(uv\) 算出實際紋理坐标對應的顔色,然後着色到該 \(uv\) 對應的頂點上。看起來就像這樣(請忽略我糟糕的ps技術):
有了足夠的了解後,我們可以解析 obj 檔案,然後将其對應紋理貼上去!
由于多出來了紋理坐标,需為原Model類增加一個存儲uv坐标的數組,将存儲面片的容器類型改一下(要為每個頂點配對一個uv點尋址順序)。另外便是增加取得uv坐标的函數:
有了紋理坐标,便可以為點着色了。我首先用了兩種算法進行插值着色,第一種為算出面片的三個頂點對應的紋理顔色,然後在其内部對這些顔色進行插值:(虛線代表真實映射,箭頭線代表插值得到)
用這種方法渲染出來的頭部是這樣的:(左邊未加光源)
看起來有模有樣了,但是你會發現似乎少了很多細節,糊糊的。那是因為三角面片内部的顔色是估算出來的,不是實際顔色。
第二種算法為算出面片三個頂點對應的 \(uv\) 坐标,然後在其内部對 \(uv\) 進行插值,然後再擷取準确的顔色:
因為多了一個步驟,也就是再對内部進行一次 \(uv\) 插值,然後再得到顔色,這樣硬算出來的真實坐标取得的顔色才會更準确:
非常棒,現在紋理映射變得非常精确!
這是我送出的本章代碼 github