電路闆排列問題是大規模電子系統設計中提出的實際問題.
該問題是: 将n塊電路闆以最佳排列方案插入帶有n個插槽的機箱中. n塊電路闆的不同的排列方式對應于不同的電路闆插入方案.
将n塊電路闆以最佳排列方式插入帶有n個插槽的機箱中。n塊電路闆的不同排列方式對應于不同的電路闆插入方案。設B={1, 2, …, n}是n塊電路闆的集合,L={N1, N2, …, Nm}是連接配接這n塊電路闆中若幹電路闆的m個連接配接塊。Ni是B的一個子集,且Ni中的電路闆用同一條導線連接配接在一起。設x表示n塊電路闆的一個排列,即在機箱的第i個插槽中插入的電路闆編号是x[i]。
x所确定的電路闆排列Density (x)密度定義為跨越相鄰電路闆插槽的最大連線數。
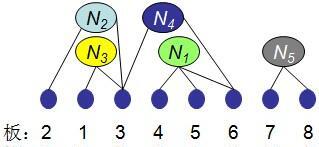
如圖,設n=8, m=5,給定n塊電路闆及其m個連接配接塊:
B={1, 2, 3, 4, 5, 6, 7, 8},N1={4, 5, 6},N2={2, 3},N3={1, 3},N4={3, 6},N5={7, 8};其中兩個可能的排列如圖所示,則該電路闆排列的密度分别是2,5。
比如:
對于第一幅圖,可以看到跨越插槽2,3的有N2,N3兩根導線(注意:一個連接配接塊上的電路闆由一根導線連接配接而成)
跨越插槽4,5的有N4,N1兩根導線,同理可得跨越插槽5,6的也是N4,N1兩根導線.
其餘所有的相鄰兩個插槽都隻跨越了一根導線,
故最終得到的密度就為2.
對于第二幅圖,跨越插槽4,5的有N1,N2,N3,N4,N5五條導線.
跨越插槽3,4的有N3,N4,N1,N5四條導線,其它的就不舉例了.最終密度為5
這樣大家對于密度的定義是不是有了清晰的了解.
電路闆排列問題是NP難問題,是以不大可能找到解此問題的多項式時間算法。
考慮采用回溯法系統的搜尋問題解空間的排列樹,找出電路闆的最佳排列。
設用數組B表示輸入。
B[i].[j]的值為1當且僅當電路闆i在連接配接塊Nj中。設total[j]是連接配接塊Nj中的電路闆數。對于電路闆的部分排列x[1:i],設now[j]是x[1:i]中所包含的Nj中的電路闆數。
由此可知,連接配接塊Nj的連線跨越插槽i和i+1當且僅當now[j]>0且now[j]!= total[j]。用這個條件來計算插槽i和i+1間的連線密度。
劃重點!!!
對于這個條件的了解至關重要,我想了很久.
我們可以拿上面第一幅圖來看:
先看now[j]>0,(now[j]表示的是x[1:i]中所包含的Nj的電路闆數),now[j]大于零表示前面的i個插槽中有連接配接塊j的電路闆存在,很好了解.
now[j] != total[j]這裡,如果目前面的i個插槽中已經用去了連接配接塊j中的所有電路闆,那麼就是說剩下的插槽不可能再有連接配接塊j的電路闆了,也就不可能再被跨越!
同樣的,一個插槽最多被一條導線跨越一次,比如上圖1中,對于5,6号插槽來說,N1隻跨越5,6插槽一次!故最大我們能夠得到的密度為m,也就是每根導線都跨越了某個相鄰槽,比如圖2.
代碼如下:
針對第一個圖示範所得的結果:
運作結果:
我想清楚這題,人沒了家人們,/(ㄒoㄒ)/~~
上課沒聽懂,放了好久才回來寫題解.排列樹我就不畫了,畫出來人要沒了.
這題也可以将cd作為類的資料成員,進而減少Backtrack函數的傳入參數,不過對效率并沒有什麼優化.
大夥應該能夠看懂吧...
歡迎大家通路我的個人部落格 --- 喬治的程式設計小屋,和我一起努力進步吧!