在上一篇《XGBoost 源碼閱讀筆記(1)--代碼邏輯結構》中向大家介紹了 XGBoost 源碼的邏輯結構,同時也簡單介紹了 XGBoost 的基本情況。本篇将繼續向大家介紹 XGBoost 源碼是如何構造一顆回歸樹,不過在分析源碼之前,還是有必要先和大家一起推導下 XGBoost 的目标函數。本次推導過程公式截圖主要摘抄于陳天奇的論文《XGBoost:A Scalable Tree Boosting System》。在後續的源碼分析中,會省略一些與本篇無關的代碼,如并行化,多線程。
XGBoost 和以往的 GBT(Gradient Boost Tree) 不同之一在于其将目标函數進行了二階泰勒展開,在模型訓練過程中使用了二階導數加快其模型收斂速度。與此同時,為了防止模型過拟合其給目标函數加上了控制模型結構的懲罰項。
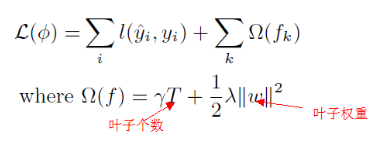
圖 1-1 目标函數
目标函數主要有兩部分組成。第一部分是表示模型的預測誤差;第二部分是表示模型結構。當模型預測誤差越大,樹的葉子個數越多,樹的權重越大,目标函數就越大。我們的優化目标是使目标函數盡可能的小,這樣在降低預測誤差的同時也會減少樹葉子的個數以及降低葉子權重。這也正符合機器學習中的"奧卡姆剃刀"原則,即選擇與經驗觀察一緻的最簡單假設。
圖 1-1 的目标函數由于存在以函數為參數的模型懲罰項導緻其不能使用傳統的方式進行優化,是以将其改寫成如下形式
圖 1-2 改變形式的目标函數
圖 1-2 與圖 1-1 的差別在于圖 1-1 是通過整個模型去優化函數,而圖 1-2 的優化目标是每次疊代過程中構造一個使目标函數達到最小值的弱分類器,從這個過程中就可以看出圖 1-2 使用的是貪婪算法。将圖 1-2 中的預測誤差項在$y_i^{t-1}$處進行二階泰勒展開:
圖 1-3 二階泰勒展開
并省去常數項
圖 1-4 省去常數項
圖 1-4 就是每次疊代過程中簡化的目标函數。我們的目标是在第 t 次疊代過程中獲得一個使目标函數達到最小值的最優弱分類器,即$f_t(x)$。在這裡累加項 n 是樣本執行個體的個數,為了使編碼更加友善,定義一個新的變量表示表示葉子 j 的所有樣本執行個體$x_i$
圖 1-5 新的變量
同時展開目标函數的模型懲罰項,并以葉子為緯度可以改寫成
圖 1-6 以葉子為緯度的目标函數
這裡函數 f 是将對應執行個體歸類到對應的葉子下,并傳回該執行個體在目前葉子下的權重 w。圖 1-6 對葉子權重 w 求導,便得出最優的葉子權重 w
圖 1-7 最優的葉子權重
與此同時将權重代入目标函數,并且省去常量,便得到了目标函數的解析式
圖 1-8 目标函數的解析式
我們的目标便是極小化該目标函數解析式。目标函數的解析式可以通過圖 1-9 清晰形象的描繪出來
圖 1-9 目标函數的解析式計算過程
從圖 1-9 可以清晰看出目标函數解析式的計算過程。目标函數的結果可以用來評價模型的好壞。這樣在模型訓練過程中,目前的葉子結點是否需要繼續分裂主要就看分裂後的增益損失 loss_change。
圖 1-10 分裂增益
增益損失 loss_change 的計算公式如圖 1-10 所示,它是由該結點分裂後的左孩子增益加上右孩子增益減去該父結點的增益。這樣在選擇分裂點時候就是選擇增益損失最大的分裂點。而尋找最佳分裂點是一個非常耗時的過程,上一篇《XGBoost 源碼閱讀筆記(1)--代碼邏輯結構》介紹了幾種 XGBoost 使用的分裂算法,這裡選擇其中最簡單的 Exact Greedy Algorithm 進行講解:
圖 1-11 Exact Greedy Algorithm
圖 1-11 算法的大意是周遊每個特征,在每個特征中選擇該特征下的每個值作為其分裂點,計算增益損失。當周遊完所有特征之後,增益損失最大的特征值将作為其分裂點。由此可以看出這其實就是一種窮舉算法,而整個樹構造過程最耗時的過程就是尋找最優分裂點的過程。但是由于該算法簡單易于了解,是以就以該算法來向大家介紹 XGBoost 源碼樹構造的實作過程。
如果對推導過程讀起來比較吃力的話也沒關系,這裡主要需要記住的是每個結點增益和權值的計算公式。增益是用來決定目前結點是否需要繼續分裂下去,而結點權值的線性組合即是模型最終的輸出值。是以隻要記住這兩個公式就不會影響源碼的閱讀。
在上一篇結尾的時候說過源碼最終調用過程如下:
這裡簡化後的源碼如下:
gpair 是一個 vector 向量,儲存了對應樣本執行個體的一階導數和二階導數。p_fmat 是一個指針,指向對應樣本執行個體的特征,new_trees 用于存儲構造好的回歸樹。
InitUpdater() 是為了初始化 updaters, 在上一篇文章也說過 updaters 是抽象類 Class TreeUpdater 的指針對象,定義了基本的 Init 和 Update 接口,該抽象的派生類定義了一系列樹構造和剪枝方法。這裡主要介紹其派生類 Class ColMaker,該類使用的即使我們前面介紹的 Exact Greedy Algorithm。
在 Class ColMaker 定義了一些資料結構用于輔助樹的構造。
XGBoost 的樹構造類似于 BFS(Breadth First Search),它是一層一層的構造樹結點。是以需要一個隊列 qexpand_用來儲存目前層的結點,這些結點會根據增益損失 loss_change 決定是否需要分裂形成下一層的結點。
在 Class ColMaker 中定義了一個 Class Builder 類,所有的構造過程都由這個類完成。
在以上代碼中核心部分就是第一個循環裡面的四個函數。我們首先來看下 Builder::InitNewNode 是如何初始化結點的增益和權值。
(1) Builder::InitNewNode()
這裡點的 root_gain 就是前面說的結點增益,将用于判斷該點是否需要分裂。weigtht 就是目前點的權值,最終模型輸出就是葉子結點 weight 的線性組合。CalGain() 和 CalWeight() 是兩個模版函數,其簡化的源碼如下:
以上兩個函數就是實作了我們一開始推導的兩個公式,即計算結點的增益和權重。在初始化隊列中的結點後,就需要對隊列中的每個結點周遊尋找最優的分裂屬性。
(2)XGBoost::Builder::FindSplit()
分裂過程最終調用了 EnumerateSplit() 函數,為了便于了解對代碼變量名做了修改,其簡化的代碼如下
從上述代碼可以很清晰看出整個代碼的流程思路就是之前介紹的 Exact Greedy Alogrithm. 這裡需要說明尋找分裂點有兩個方向,一個是從左到右尋找,一個是從右到左尋找。上述代碼隻展示了一個方向的尋找過程。在尋找特征分裂門檻值的時候分裂增益的計算函數是 CalcSplitGain(),其具體代碼如下:
上述代碼就是簡單将左孩子和右孩子的增益相加,而增益損失 loss_change 就是将左右孩子相加的增益減去其父節點的增益。
(3)XGboost::Builder::ResetPosition()
在尋找到目前層各個結點的分裂門檻值之後,便可以在對應結點上構造其左右孩子來增加目前樹的深度。當樹的深度增加了,就需要将分類到目前層非葉子結點的樣本執行個體分類到下一層的結點中。這個過程就是通過 ResetPosition() 函數完成的。
(4)XGboost::Builder::UpdateQueueExpand()
XGboost::Builder::UpdateQueueExpand() 函數更新 qexpand隊列中的結點為下一層結點,然後在調用 XGboost::Builder::InitNewNode() 更新 qexpand中結點的權值和增益以便下一次循環
本篇主要詳細叙述了 XGBoost 使用 Exact Greedy Algorithm 構造樹的方法,并分析了對應的源碼。在分析源碼過程中為了便于了解對代碼做了一些簡化,如省去了其中多線程,并行化的操作,并修改了一些變量名。在上述的樹構造完成之後,還需要對樹進行剪枝操作以防止模型過拟合。由于篇幅所限,這裡就不再介紹剪枝操作。本篇文章隻是起一個抛磚引玉的引導作用,想要對 XGBoost 實作細節有更加深刻了解,還需要去閱讀 XGBoost 源碼,畢竟有些東西用文字描述遠不如用代碼描述清晰。最後歡迎大家一起來讨論。