Redis 高階資料類型重溫

今天這個專題接着上一篇 Redis 的基本資料類型繼續講解剩下的高階資料類型：BitMap、HyperLogLog 和 GEO hash。這些資料結構的底層也都是基于我們前面說的 5 種基本類型，但是實作上有很多 Redis 自己的創意。下面我們一起進入高階資料結構的世界。

BitMap 從字面意義上能看出是一個位元組組成的集合。由于一個比特位隻有 0 和 1 兩種狀态，是以 BitMap 能應用的場景是有限的，隻能對這種二值的場景進行使用。BitMap 底層是怎麼實作的呢？

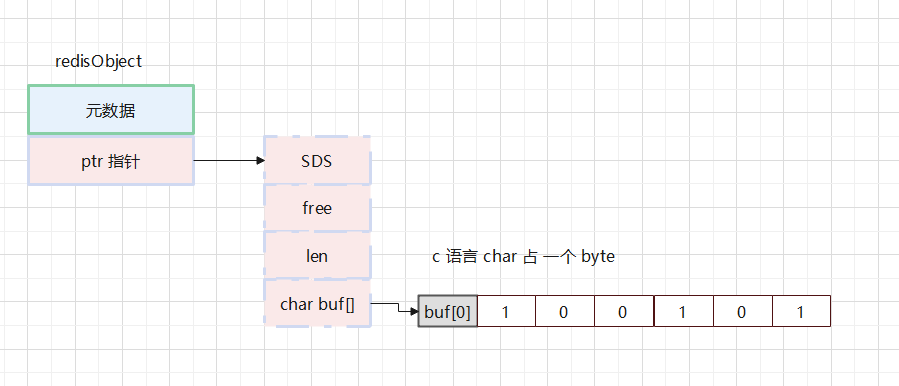
Redis 底層隻有我們上文說的 5 種基本資料類型，BitMap 并不是一種新型的資料結構，而是基于 Redis 的 string 類型的 SDS 結構來實作的。

SDS 的資料存儲在 buf 位元組數組中，1 byte = 8 bit。那麼将這個位元組數組連起來就是很多個 8 bit 組成的比特位數組。我們可以将數組的下标當做要存儲的 key，數組的值 0 或者 1 就是 value。

為了驗證這個存儲邏輯，我們可以使用 Redis 指令行來手動調試一下：

通過上面的實驗我們可以看出，BitMap 占用的空間，就是底層字元串占用的空間。假如 BitMap 偏移量的最大值是 OFFSET_MAX，那麼它底層占用的空間就是：

因為字元串記憶體隻能以位元組配置設定，是以上面的機關是位元組。

但是需要注意，Redis 中字元串的最大長度是 512M，是以 BitMap 的 offset 值也是有上限的，其最大值是：

由于 C語言中字元串的末尾都要存儲一位分隔符，是以實際上 BitMap 的 offset 值上限是：

了解了 BitMap 的實作邏輯以及在 Redis 中的存儲邏輯之後我們對 Redis 提供的指令應該就有了更深刻的認識。

基數估計(Cardinality Estimation) 一直是大資料領域的重要問題之一。基數估計就是為了估計在一批資料中它的不重複元素有多少個。

這個問題的應用場景非常之多，比如對于百度，谷歌這樣的大搜尋引擎，要統計每天每個地區有多少人通路網站，在這種統計中十億和十億零三千的差別并不是很大，隻需要一個近似的值即可。

如果去考慮實作，我們首先想到的就是字典。對于新來的元素，查一下是否已經屬于這個字典，不屬于則添加進去，這個字典的整體長度就是我們要的結果。方法雖然好并且還精确，但是帶來的後果就是空間複雜度會很高，資料量大的情況下，使用的空間可能超過我們的想象。

那麼是否存在一些近似的方法，可以估算出大資料的基數呢？伯努利過程可以用來做基數統計。

伯努利過程就是一個抛硬币實驗的過程。抛一枚硬币隻會有兩種結果：正面，反面，機率都是 1/2。伯努利過程就是一直抛硬币直到出現正面為止，并記錄下此時抛擲的次數 K。比如說抛一次硬币就出現了正面， k = 1；或者直到第三次才出現正面，那麼 k=3。伯努利試驗是在同樣的條件下重複地、互相獨立地進行的一種随機試驗，其中“在相同條件下”意在說明：每一次試驗的結果不會受其它實驗結果的影響，事件之間互相獨立。

對于 n 次伯努利實驗，我們會得到 n 個出現正面的投擲次數，k1, k2,k3...kn。這其中最大的值是 kmax，接下來我們省略一大堆數學推導過程，直接來到結論的部分：

n = 2 kmax

即可以根據最大投擲次數來近似估計進行了幾次伯努利過程。比如：

第一次實驗：抛 3 次出現正面，k = 3，n = 23;

第二次實驗：抛 2 次出現正面，k = 2，n = 22；

第三次實驗：抛 5 次出現正面，k = 5，n = 25；

......

第 n 次實驗：抛 7 次出現正面，k = 7，我們根據公式可以預估 n = 27。

根據上面的示例大家基本了解伯努利過程是什麼。在實驗次數較少的條件下（即進行伯努利過程次數少的情況）我們預估出來的 n 值肯定是有較大誤差的。比如上面的抛硬币實驗一共就進行了 3 次就出現了正面，此時你預估 n=23 這個值可能跟再抛多次出現的值有一定的誤差。

Redis 中的 HyperLogLog 就是基于伯努利過程的原理來統計集合基數的，當然對于消除誤差， Redis 也做了一些處理。

HyperLogLog 基于 LogLog Counting 算法改進而來。在添加元素的時候，HyperLogLog 通過 MurmurHash64A 算法給元素計算出一個 64bit 的 hash 值來模拟伯努利過程。

例如 17， hash Value = 10001，hash value 總共是64 bit 是以前面的位置都是 0。這些 byte 位就類似于一次抛硬币的伯努利過程，0 代表抛硬币落地式反面，1 代表抛硬币落地式正面。LogLog Counting 的基本思想是：

對每個待測集合中的元素 x，計算它的哈希值 hash = H(x)；

将哈希值 hash 通過它們的前 k=logm 個比特分組（即分桶），作為桶的編号，即一共有 m 個桶；

将 hash 的後 L - k 個比特作為真正參與基數估計的串 s，計算并記錄下所有桶内的 ρ(s)；

令 M[k] 表示第 k 個桶内所有元素中最大的那個 ρ 值，那麼該集合基數的估計量為：

Ñ = αm · m · 2ΣM[i] / m

其中 αm 是修正參數。

LogLog Counting 在誤差精簡上并沒有比它的前輩 F-M 算法小，反而還大了。但是它真正有意義的是降低了空間複雜度，F-M 算法中用 logN 個比特位來存儲 hash 值，而 LogLog Counting 算法隻存儲下标（即 ρ 值）。可以降低為 log(logN) 個比特位，再加上分桶數為 m，是以空間複雜度為：

O[m* log(logN)]

這也是 LogLog Counting 算法名字的由來。

Redis 基于節省記憶體空間的原因在 LogLog Counting 算法的基礎上做了一些優化，優化的目的是減少誤差和變态地更加節省記憶體！Hyper 是“超越”的含義，那麼HyperLogLog 到底比前輩超越在哪裡呢？

第一是分桶幾何平均數改為計算 m 個桶的調和平均數。

調和平均數

調和平均數差別于幾何平均數概念。幾何平均數=總數/個數，但是會有一個問題：馬雲的平均年收入是100 億，我的平均年收入是 0.00000001 億，我和馬雲的平均年收入是100億，沒毛病。

使用調和平均數就能解決這個問題，調和平均數的結果會趨向于集合中比較小的數，x1 到 xn 的調和平均數符合如下公式：

根據這個公式計算我和馬雲的平均工資：

平均工資 = 2 / (1/1億 + 1/0.00000001億) = 20元

這樣算起來，我還能接受！

幾何平均值受離群值（偏離均值很大的值）的影響非常大，分桶的空桶越多，LLC 的估計值就越不準。使用調和平均值就不會受這種影響。

第二是根據基數估值的大小采用不同的估計方法進行修正。論文中給出了在常見情況：即被估集合的基數在億級别以下，m 取值在 2[4, 16] 區間下的修正的算法。

對應到 Redis 代碼實作，Redis 使用了 214 = 16384個桶，按照标準差誤差為 0.81%，精度相當高。HLL 将 64 bit 的低 14 位拿出來作為對應桶的序号，14 bit 可以表示 214 = 16384 個桶。剩下的 50 個比特用來做基數估計。而 26=64，是以隻需要用 6 個比特表示下标值。

假設一個字元串的前 14 位是：00 0000 0000 00110，十進制 = 6，那麼該基數将會被放到編号為 6 的桶中。在一般情況下，一個 HLL 資料結構占用記憶體的大小為16384 * 6 / 8 = 12kB，Redis将這種情況稱為密集（dense）存儲。

為了更高效的說清楚 Redis 的實作，我們先看 Redis 對 HLL 的定義,Redis 使用 hllhdr 來持有一個 HLL：

從上述結構體可以大緻看出，Redis 實作的 HLL 結構大緻分為兩部分：

頭部資訊

存儲桶資料的 registers

為了減少計算的成本，Redis 的 HLL 實作使用 card 來儲存基數估計的最新計算結果，card 字段采用小端存儲，用最高有效位來辨別 card 記憶體儲的結果是否還有效。由于 Redis 的 HLL 實作使用了 16384 個分組，基于前文所述的 HLL 的标準差計算方法，Redis 的 HLL 實作的誤差是

，也就是 Redis 官方文檔中公布的誤差率。

encoding 辨別目前 HLL 結構所使用的編碼方式，一共有兩種：

sparse(稀疏存儲)

dense(密集存儲)

稀疏存儲

在 HLL 初始化的時候資料量很少，如果還是使用固定位數來存儲 16384 個桶的話大量的空間就被浪費。是以 Redis 使用稀疏編碼(HLL_SPARSE)初始化一個新的 HLL 結構，它是具有壓縮性質的編碼，将重複的分組計數壓縮成操作碼(opcode)，以此降低記憶體使用。為了節省空間 Redis 會将連續的全 0 桶壓縮成 0 桶計數值。該計數值可以用單位元組或雙位元組表示，高 2bit 為标志位，是以可以分别表示連續 64 個全 0 桶和連續 16384 個全 0 桶。

稀疏編碼使用 ZERO、XZERO、VAL 三種操作碼對registers存儲的資料進行編碼，其中 ZERO、VAL 占一個位元組，XZERO 占兩個位元組：

當多個連續桶的計數值都是零時，Redis 提供了幾種不同的表達形式：

ZERO：操作碼為<code>00xxxxxx</code>，字首兩個零表示接下來的 6bit 整數值加 1 就是零值計數器的數量，注意這裡要加 1 是因為數量如果為零是沒有意義的。6位 xxxxxx 表示有 1 到 64(111111+1，0 沒有意義)個連續分組為空。比如 <code>00010101</code> 表示連續 <code>22</code> 個零值計數器。

XZERO：操作碼表示為<code>01xxxxxx yyyyyyyy</code>，6bit 最多隻能表示連續 <code>64</code> 個零值計數器，這樣擴充出的 14bit 可以表示最多連續 <code>16384</code> 個零值計數器。這意味着 HyperLogLog 資料結構中 <code>16384</code> 個桶的初始狀态，所有的計數器都是零值，可以直接使用 2 個位元組來表示。

VAL：操作碼表示為<code>1vvvvvxx</code>，中間 5bit 表示計數值，尾部 2bit 表示連續幾個桶。它的意思是連續 <code>(xx +1)</code> 個計數值都是 <code>(vvvvv + 1)</code>。比如 <code>10101011</code> 表示連續 <code>4</code> 個計數值都是 <code>11</code>。

注意上面第三種方式的計數值最大隻能表示到 <code>32</code>，而 HLL 的密集存儲單個計數值用 6bit 表示，最大可以表示到 <code>63</code>。當稀疏存儲的某個計數值需要調整到大于 <code>32</code> 時，Redis 就會立即轉換 HLL 的存儲結構，将稀疏存儲轉換成密集存儲。

密集存儲

HLL 的密集編碼(HLL_DENSE)結構是由稀疏編碼轉換而來的，它的結構相對簡單，由連續 16384 個桶拼接而成，每個組占用 6 位(16384×6/8，12KB的由來)。不過由于存儲采用的是小端模式，是以每個桶的 6bit 計數值是從 LSB(低位) 開始一個接一個地編碼到 MSB(高位)(差別于大端模式即正常的數字是從左到右依次是高位到低位，小端模式是從左到右依次是低位到高位)。

密集存儲涉及到一個定位位元組的問題，因為一個桶是 6bit，而一個位元組是 8bit，那麼必然會涉及到一個位元組持有兩個桶的情況。這種情況下給定一個桶的編号如何定位到對應的桶呢？

假設桶的編号為 idx，這個 6bit 計數值的起始位元組位置偏移用 offset_bytes 表示，它在這個位元組的起始比特位置偏移用 offset_bits 表示。我們有：

前者是商，後者是餘數。比如 bucket 2 的位元組偏移是 1，也就是第 2 個位元組。它的位偏移是4，也就是第 2 個位元組的第 5 個位開始是 bucket 2 的計數值。需要注意的是位元組位序是左邊低位右邊高位。

如果 offset_bits 小于等于 2，那麼這 6bit 在一個位元組内部，可以直接使用下面的表達式得到計數值 val

如果 offset_bits 大于 2，那麼就會跨越位元組邊界，這時需要拼接兩個位元組的位片段。

總體來說，HLL 存儲結構将記憶體使用優化到極緻，以 12k 的空間來估算最多 264 個不同元素的基數。并且優化了基數結果的誤差範圍為 0.81 %。如果我們有海量資料查詢的需求，可以考慮使用 HLL。

GEO 算法是一種地理位置距離排序算法，将二維的經緯度資料映射到一維的整數上。這樣所有的元素都将挂載到一條線上，距離靠近的二維坐标映射到一維後的點之間距離會很接近。當我們想要計算附近的人時，首先将目标位置映射到這條線上，然後在這條一維的線上擷取附近的點就行。

對應到我們的地球經緯度資訊來說，緯度區間為[-90, 90]，經度區間為 [-180,180]。如何将二維的坐标轉換為一維的值呢？下面我們一起示範一下目前的處理手段。首先我們把地球經緯度坐标展開為一張平面：

首先我們将整幅地圖分割成四個小塊，然後用簡單的 01 編碼來辨別每個小塊：

這樣整個地圖被我們分割為 4 個空間，每個空間用一維的 01 來辨別。如果地點 A 坐落于 00 空間，那麼它的一維辨別就是 00。當然你會說這麼大一塊空間都用 00 辨別這範圍也太大了吧。既然我們可以分割為 4 塊，你是不是順推就知道我們可以繼續分割為 8,16,100，甚至更大都可以，這樣我們每一塊空間所辨別的範圍更精确，搜尋地理位置也更精确。

根據這個原理我們可以通過最小逼近的準則來用一維字元串表達相似準确的最小位置。比如北京市區坐标為：北緯39.9”，東經116. 3”，那麼我們可以按照如下算法對北京的經緯度進行逼近編碼：

緯度區間為[-90, 90]，一分為二為[-90, 0),[0 , 90]，稱為左右區間，北京在北緯 39.9，那麼在右區間，給标記為 1；

接着将區間[0, 90] 二分為[0, 45), [45, 90]，可以确定 39.9 在左區間，标記為 0；

遞歸上述過程，可以确定 39.9 總是屬于某個細小的區間 [x, y]，随着疊代的越多，那麼這個區間會越來越逼近 39.9 ；

通過對緯度這樣劃分，屬于左區間記錄 0 ，屬于右區間記錄 1，那麼最終會得到一個關于緯度的 01 編碼，編碼長度取決于區間劃分的粒度。

同理經度也是如此劃分。

假設經過上述計算，緯度産生的編碼為 1001000101，經度産生的編碼為 0100100101。我們把經緯度組合成一個串，這個串的偶數位放經度，奇數位放緯度，把兩串編碼組合成一個新串：

01100001100000110011

最後使用用 0-9、b-z（去掉a, i, l, o）這 32 個字母進行 base32 編碼，首先将 01100 00110 00001 10011 轉成十進制，對應着 12、6、1、19 十進制對應的編碼就是：MGBT。同理，将編碼轉換成經緯度的解碼算法與之相反。

RFC 4648 Base32 字母表

值

符号

填充

通過這種加密之後我們就把經緯度轉換為很短的幾個字母來表示。

空間填充曲線

上面我們将空間劃分為很多個小範圍之後，我們是按照範圍從大到小進行逼近，那麼對應到地圖逼近的順序是什麼呢？這裡就提到了空間曲線的概念，即我們從哪裡開始周遊，周遊的順序又是如何。

在數學分析中，有這樣一個難題：能否用一條無限長的線，穿過任意次元空間裡面的所有點？常見的有： Z階曲線(Z-order curve)、皮亞諾曲線（Peano curve）、希爾伯特曲線（Hilbert curve），之後還有很多變種的空間填充曲線，龍曲線(Dragon curve)、高斯帕曲線(Gosper curve)、Koch曲線(Koch curve)、摩爾定律曲線(Moore curve)、謝爾賓斯基曲線(Sierpiński curve)、奧斯古德曲線(Osgood curve)等。

Z 階曲線（Z-order curve）是 GEO hash 目前再用的空間填充曲線：

這個曲線比較簡單，生成也比較容易，秩序要把每個 Z 首位相連即可。 Geohash 能夠提供任意精度的分段級别。一般分級從 1-12 級。利用 Geohash 的字元串長短來決定要劃分區域的大小，一旦標明 cell 的寬和高，那麼 Geohash 字元串的長度就确定下來了。地圖上雖然把區域劃分好了，但是還有一個問題沒有解決，那就是如何快速的查找一個點附近鄰近的點和區域呢？

Geohash 有一個和 Z 階曲線相關的性質，那就是一個點附近的地方(但不絕對) hash 字元串總是有公共字首，并且公共字首的長度越長，這兩個點距離越近。由于這個特性，Geohash 就常常被用來作為唯一辨別符。用在資料庫裡面可用 Geohash 來表示一個點。Geohash 這個公共字首的特性就可以用來快速的進行鄰近點的搜尋。越接近的點通常和目标點的 Geohash 字元串公共字首越長（特殊情況除外）。

前面說 Geohash 編碼的時候提到 Geohash 碼生成規劃： “偶數位放經度，奇數位放緯度”。這個規則就是 Z 階曲線。看下圖：

x 軸就是緯度，y 軸就是經度。經度放偶數位，緯度放奇數位就是這樣而來的。

但是 Z 階曲線有個問題：它的突變性問題會導緻某些編碼位置相鄰但是距離缺很遠。比如上圖中的 001000 和 000111，編碼相鄰，距離卻很大。

除了 Z 階曲線外，勞工效果最好的是 Hilbert Curve 希爾伯特曲線，希爾伯特曲線是一種能填充滿一個平面正方形的分形曲線（空間填充曲線），由大衛·希爾伯特在 1891 年提出。由于它能填滿平面，它的豪斯多夫維是2。取它填充的正方形的邊長為 1，第 n 步的希爾伯特曲線的長度是 2n - 2(-n)。

一階的希爾伯特曲線，生成方法就是把正方形四等分，從其中一個子正方形的中心開始，依次穿線，穿過其餘 3 個正方形的中心。如下圖：

二階的希爾伯特曲線，生成方法就是把之前每個子正方形繼續四等分，每 4 個小的正方形先生成一階希爾伯特曲線。然後把 4 個一階的希爾伯特曲線首尾相連。

n 階的希爾伯特曲線的生成方法也是遞歸的，先生成 n-1 階的希爾伯特曲線，然後把 4 個 n-1 階的希爾伯特曲線首尾相連。

希爾伯特曲線空間曲線的優點在于對多元空間有效的降維。如下圖就是希爾伯特曲線在填滿一個平面以後，把平面上的點都展開成一維的線了。另外希爾伯特曲線是連續的，是以能保證一定可以填滿空間。

Redis 沒有選擇效果更好的希爾伯特曲線來實作低位位置劃分而是使用 Z 階曲線這個官方并沒有說明，大概隻是 Z 階曲線的實作相對來說要簡單一些。另外關于 Z 階曲線邊界點距離問題，Redis 也有修正，除了使用定位點的 GEOhash 編碼之外，目前比較通行的做法就是我們不僅擷取目前我們所在的矩形區域，還擷取周圍 8 個矩形塊中的點。那麼怎樣定位周圍 8 個點呢？關鍵就是需要擷取周圍 8 個點的經緯度，那我們已經知道自己的經緯度，隻需要用自己的經緯度減去最小劃分機關的經緯度就行。因為我們知道經緯度的範圍，有知道需要劃分的次數，是以很容易就能計算出最小劃分機關的經緯度。

通過上面這張圖，我們就能很容易的計算出周圍 8 個點的經緯度，有了經緯度就能定位到周圍 8 個矩形塊。這樣我們就能擷取包括自己所在矩形塊的 9 個矩形塊中的所有的點。最後分别計算這些點和自己的距離（由于範圍很小，點的數量就也很少，計算量就很少）過濾掉不滿足條件的點就行。

在 Redis 中，查找某個中心地理位置（longitude,latitude）周圍 radius 範圍内的點，先根據 latitude 和 radius 計算出經緯度二進制編碼的長度 step，即劃分的次數，然後根據中心地理位置（longitude,latitude）、radius、step 計算出中心位置的二進制編碼，再計算出周邊 8 個位置塊的二進制編碼，再依次計算 9 個位置塊中的點是否滿足距離要求。

GEOhash 在 Redis 中的實作方式如下：

long_range 和 lat_range 為地球經緯度的範圍；hash->bits 使用者儲存最終二進制編碼結果，hash->step 是經緯度劃分的次數，在 Redis 中該值為 26，即經度/緯度的二進制編碼長度為 26，最終經交叉組合而成的地理位置的二進制編碼為 52 位。Base32 編碼為每 5bits 組成一個字元，是以最終的 GeoHash 字元串為 11 位。

為什麼是 52 位？因為在 Redis 中是把地理位置編碼後的二進制值存入 zset 資料結構中，double 類型的尾數部分長度為 52 位。

上述算法在分别計算經度/緯度的二進制編碼時，是先計算所求地理位置的經度/緯度在整個經度/緯度範圍内的偏移，再乘以 2 的 step 次方。劃分 step 次，會得到 2 的 step 次方個區域，區域值為 0 -（1<<step-1），是以偏移乘以 2 的 step 次方即可得到劃分 step 次時改經度/緯度的二進制編碼。

Redis 中處理這些地理位置坐标點的思想是: 二維平面坐标點 --> 一維整數編碼值 --> zset(score為編碼值) --> zrangebyrank(擷取score相近的元素)、zrangebyscore --> 通過score(整數編碼值)反解坐标點 --> 附近點的地理位置坐标。