1.邊緣檢測:
邊緣檢測是圖像處理和計算機視覺中的基本問題,邊緣檢測的目的是辨別數字圖像中亮度變化明顯的點。圖像屬性中的顯著變化通常反映了屬性的重要事件和變化。這些包括(i)深度上的不連續、(ii)表面方向不連續、(iii)物質屬性變化和(iv)場景照明變化。
邊緣檢測是圖像處理和計算機視覺中,尤其是特征提取中的一個。
圖像邊緣檢測大幅度地減少了資料量,并且剔除了可以認為不相關的資訊,保留了圖像重要的結構屬性。有許多方法用于邊緣檢測,它們的絕大部分可以劃分為兩類:基于查找的一類和基于零穿越的一類。基于查找的方法通過尋找圖像一階導數中的最大和最小值來檢測邊界,通常是将邊界定位在梯度最大的方向(想想一階導數的含義是圖像變化的速度,最大的自然就是變化最大的了)。基于零穿越的方法通過尋找圖像二階導數零穿越來尋找邊界,通常是Laplacian過零點或者非線性差分表示的過零點。
2.差分
差分
,是數學中的一個概念。它将原函數
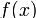
到
中重要的一個概念。差分的定義分為前向差分
和逆向差分
兩種。
函數的前向差分通常簡稱為函數的差分。對于函數
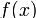
,如果:
,
則稱
為
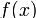
的解法相似。當
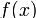
。前向差分會将多項式階數降低1。
對于函數
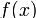
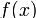
的一階逆向差分。
3.索貝爾算子
索貝爾算子
算子,用來運算圖像亮度函數的梯度之近似值。在圖像的任何一點使用此算子,将會産生對應的梯度矢量或是其法矢量。
,即可分别得出橫向及縱向的亮度差分近似值。如果以
代表原始圖像,
及
分别代表經橫向及縱向邊緣檢測的圖像,其公式如下:
圖像的每一個像素的橫向及縱向梯度近似值可用以下的公式結合,來計算梯度的大小。
然後可用以下公式計算梯度方向。
在以上例子中,如果以上的角度Θ 等于零,即代表圖像該處擁有縱向邊緣,左方較右方暗。
4.矩陣卷積
函數矩陣的卷積
定義兩個函數矩陣的卷積可以用類似于兩個矩陣乘法的運算規則,即将兩個元素相乘的符号都用卷積來替換,譬如
5.圖像梯度
感性認識:梯度值就是圖像灰階值的顯著變化的地方。不同的算子對應了不同的求梯度的方法:
以Sobel算子(效果較好)為例:
對于數字圖像,可以用一階差分代替一階微分;
△xf(x,y)=f(x,y)-f(x-1,y);
△yf(x,y)=f(x,y)-f(x,y-1)
求梯度時對于平方和運算及開方運算,可以用兩個分量的絕對值之和表示,即:
G[f(x,y)]={[△xf(x,y)] +[△yf(x,y)] } |△xf(x,y)|+|△yf(x,y)|;
Sobel梯度算子是先做成權重平均,再微分,然後求梯度,即:
△xf(x,y)= f(x-1,y+1) + 2f(x,y+1) + f(x+1,y+1)- f(x-1,y-1) - 2f(x,y-1) - f(x+1,y-1);
△yf(x,y)= f(x-1,y-1) + 2f(x-1,y) + f(x-1,y+1)- f(x+1,y-1) - 2f(x+1,y) - f(x+1,y+1);
G[f(x,y)]=|△xf(x,y)|+|△yf(x,y)|;
6.高斯金字塔
對于大小為w×i 的圖像I,高斯金字塔Gj 由I的幾個分辨率減小的高斯圖像Ii(i是下标,下同) 組成,其中,i={0,1,...,j}代表金字塔的級數. 圖像Ii 的大小為(w/2i)×(h/2i).[2i表示2的i次方]。
圖像Ii 是通過對圖像Ii-1(i-1是下标) 進行隔行隔列采樣而得到的圖。