本文将對 <code>func_treelize</code> 這一treevalue庫中的核心功能進行詳細的原了解析。
關于treevalue的概述,可以參考之前的文章:Treevalue(0x01)——功能概述
在treevalue庫中, <code>func_treelize</code> 是核心特性之一,可以将普通的函數快速作用于樹對象上。而這一“作用”的原理是什麼呢,我們來一起看看——首先準備一個普通的函數,并加上 <code>func_treelize</code> 裝飾器,就像這樣
函數的部分是一個最大公因數的計算,并且和之前文章(Treevalue(0x01)——功能概述)中的差別在于,添加了一行 <code>print</code> 輸出,用于展現函數内部在整個計算過程中是如何被調用的。基于這一函數,我們進行如下的調用,可以得到對應的輸出結果
根據輸出語句,不難發現——經過<code>func_treelize</code>裝飾後的函數,在被傳入<code>TreeValue</code>類型的時候,會自動基于其結構将内部的數值一一對應傳入原函數,并在執行計算後組裝成與原來相同的樹結構。
基于以上基本特性,<code>func_treelize</code>這一過程也被稱為函數的樹化,經過樹化後的函數将滿足以下基本特性:
當所有傳入參數均為非樹對象時,函數行為與傳回值與原函數保持嚴格一緻,即樹化後的函數依然可以像原函數一樣地使用。
樹化的函數本身不會對傳入的樹對象内部結構有顯式的限制,在函數的樹化邏輯中将基于傳入樹參數的結構生成最終的傳回值結構。
函數的樹化邏輯部分不會對樹對象内部的值進行任何的判定與檢測,隻是作為一個中繼器将對應的值傳入原函數并擷取運算結果。
通過開頭章節的簡單例子展示,相信各位已經對函數的樹化有了基本的概念和了解。在本章中,将對函數的樹化過程進行更加詳細的機制分析。
在開頭章節的例子中,展現的隻是兩種最為理想化的情況:
傳入的參數均為非樹對象
傳入的參數均為結構完全一緻的樹對象
然而實際上,基于對“樹”這一資料結構的基本了解,不難發現實際上需要作出處理的情況依然有很多,包括但不限于:
鍵值缺少——參與計算的某個樹對象在對應的位置上缺少了對應的鍵值,這樣的情況如何處理?例如下圖中, <code>t2.x.d</code> 缺失,這樣的情況該如何處理?
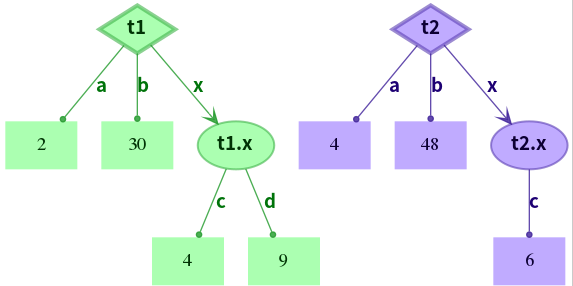
鍵值類型不比對——參與計算的某幾個樹對象對應位置上,有些是葉子節點值,有些是非葉子節點子樹,形成“值-子樹”之間的直接運算,這樣的情況如何定義?例如下圖中, <code>t1.b</code> 為子樹但是 <code>t2.b</code> 為值,這樣的情況如何定義?
計算模式多樣性——當參與計算的樹對象之間的結構存在較多較大差異性時,如何設計計算政策使之能支援更多樣化的計算?例如下列的場景,如何組織對如此結構各異的樹之間的運算?
資料格式多樣性——當參與計算的葉子節點值格式存在不統一時,如何處理?例如下面的場景,如何對 <code>t1</code> 和 <code>t2</code> 下顯然不同尺寸的 <code>torch.Tensor</code> 進行處理?
是以,基于這些很現實的問題,我們為樹化函數定義了如下的選項:
模式選項(mode)——決定樹化函數的整體運作機制。
繼承選項(inherit)——對鍵值類型不比對的情況進行了定義,并提供了處理機制。
預設選項(missing)——為鍵值缺少的情況提供了預設值補全機制。
模式選項是樹化函數中最為重要的選項,其将直接決定樹化函數的主體計算邏輯。目前定義了四種常用模式:
嚴格模式(STRICT)
内共同模式(INNER)
外共有模式(OUTER)
左優先模式(LEFT)
接下來的子章節中會結合例子進行逐一介紹。
嚴格模式是最常用的模式選項,意味着當且僅當所有樹參數在目前子樹位置上的鍵一一對應時,會将其鍵值進行一一對應地代入計算,否則抛出異常。代碼實作如下,與開頭的例子等價,模式選項的預設值即為嚴格模式
在上述的樹化gcd函數中,完整的計算機制如下圖1所示, <code>tr</code> 為樹化gcd的運算結果
(圖1,t1、t2内的鍵值可以形成一一對應)
但是當出現如下所示的參數時,則應抛出異常,因為部分鍵存在缺失,無法形成一一對應。
(圖2,t1.b與t1.x.c缺失,無法形成一一對應)
嚴格模式是一種最為常見的計算邏輯,适用于大部分常見情況,也是在業務邏輯上最為順理成章的一種模式。但是對非規則結構下的計算則不能相容,是以另外三種模式選項分别針對不同的情況來支援非規則結構下的計算。
内共同模式下,僅會對全部樹參數目前子樹位置上均存在此鍵時,才會對将其鍵值進行一一對應地代入計算,而當此鍵值在某一樹參數目前子樹位置上存在缺失情況是,則會直接忽略該組鍵值。代碼實作如下,将 <code>mode</code> 設定為 <code>inner</code> 即可
例如對圖2所示的例子,在内共同模式下可以正常計算,如圖3所示
(圖3,t1.x.c和t2.b因為t2.x.c和t1.b的缺失而被忽略)
内共同模式會忽略無法形成對應的多餘值,可以確定在幾乎所有情況下均能得出計算結果而不會産生錯誤。但是會不可避免地造成部分資訊丢失,而在一部分情況下這是不可接受的,是以請根據實際需求進行選擇。
外共有模式下,隻要在任意一個樹參數的目前子樹位置上存在此鍵值,則會将其進行代入計算。而對于缺失的值,則會使用預設選項中設定的值或生成器進行擷取并代入。代碼實作如下,将 <code>mode</code> 設定為 <code>outer</code> 即可,并将預設選項設定為值 <code>1</code>
例如對圖2所示的例子,在外共有模式下可以正常計算,如圖4所示
(圖4,t1.b和t1.x.c缺失,将使用預設選項指定的預設值1)
外共有模式将會讓所有的數值參與運算,但是在絕大部分情況下均依賴預設選項的設定,是以在使用前請確定預設選項的正确配置,以及業務邏輯上的自洽。
左優先模式下,參與運算的鍵值将以全部樹參數中最左的一項為參考。其中最左的一項定義為,在python函數調用的位置參數(postional argument)中,如果存在樹參數,則取最左的一項;如果不存在,則在函數調用的鍵值參數(key-word argument)紅,取字典序最小的一項。代碼實作如下,将 <code>mode</code> 設定為 <code>left</code> 即可,并将預設選項設定為值 <code>1</code>
例如對于圖2所示的 <code>gcd(t1, t2)</code> 例子中,在左優先模式下計算結果如下,如圖5所示
(圖5,t2.b因t1.b的缺失而被忽略,而t2.x.c取預設值1)
而在 <code>gcd(t2, t1)</code> 例子中,左優先計算結果如下,如圖6所示
(圖6,t1.x.c因t2.x.c的缺失而被忽略,而t1.b取預設值1)
左優先模式會按照最左樹參數的結構來進行計算,生成的計算結果也将和最左的參數保持一緻。但是與外共有模式類似,左優先模式在絕大部分情況下依賴預設選項的配置,需要確定配置準确無誤且自洽。此外,對于原本滿足交換律的運算,經過左優先模式的樹化後将會失去原有的交換律性質,這一點請務必留意。
繼承選項可以通過普通值的繼承機制,讓樹化函數在實際應用中使用起來更加簡潔,也讓樹參數可以和普通參數在樹化後的函數中被混用。在預設情況下,繼承選項是處于開啟狀态的,即等價于如下的代碼
是以,有如下的例子 <code>gcd(t1, t2)</code> ,其計算結果如圖7所示
(圖7,t2.x.c和t2.x.d繼承t2.x的值6)
此外顯而易見的是,也可以直接将非樹值直接傳入,和樹參數混用,例如下面的例子 <code>gcd(100, t1)</code> ,其計算結果如圖x所示
(圖8,值100被完全繼承并作為第一棵樹的全部值)
而當繼承選項被關閉時,則上述兩個例子均會抛出異常,因為存在值和子樹混用的情況。
從業務邏輯的角度來看,繼承選項可以良好地适應大部分真實存在的值複用情況,且值和子樹混用在大多數業務邏輯上也是有明确意義的。但是當混用在業務邏輯角度上意義不明且需要被顯式地檢測時,則建議關閉繼承選項。
預設選項可以為部分鍵值存在缺失的情況提供一個值的補充,主要作用于外共有模式和左優先模式。我們可以通過 <code>missing</code> 參數直接提供值,如下所示
上述的加法函數計算例子如下, <code>total(t1, t2, t3)</code> 計算結果如下圖9所示
(圖9,預設值0被全面用于填補空缺,并最終計算出了有效的總和)
此外考慮到有些情況下,直接使用值作為預設值可能會存在公用同一個對象導緻錯誤的情況,是以我們提供了通過傳入生成函數來産生預設值的用法。可以通過 <code>missing</code> 參數傳入值生成器,如下所示
上述的清單追加值計算例子如下, <code>append(t0, t1, t2, t3)</code> 運算結果如下圖10所示
(圖10,每次預設均會生成新的空清單)
通過預設選項的有效配置,結合外共有模式和左優先模式,可以有效擴充樹化函數對值預設情況的處理能力。不過值得注意的是,預設選項在嚴格模式下無法生效,因為當檢測到鍵缺失時将會直接抛出異常;以及預設模式在内共同模式下永遠無法實質上生效,是以樹化函數會針對這一情況抛出一個警告資訊。
除了上述的基本機制選項之外,樹化函數還提供了上升(rise)和下沉(subside)選項,以簡化對結構化資料的處理。兩者的功能分别為:
下沉(subside)——嘗試将參數中頂層結構非樹的對象,提取結構後将結構下沉至樹内,使原函數在運作過程中可以接收到。關于下沉函數的具體細節可以參考之前文章。
上升(rise)——嘗試從傳回結果樹的葉子節點值中提取共同結構,向上升至樹外,使傳回值的邏輯結構可以被外部直接通路。關于上升函數的具體細節可以參考之前文章。
是以我們可以在需要的時候打開這兩個選項,代碼如下,實作的效果是從清單 <code>arr</code> 中查找首個滿足條件值的位置( <code>position</code> ),并統計共有多少個滿足條件的值( <code>cnt</code> )
代碼中可以看到三棵樹 <code>t1</code> 、 <code>t2</code> 、 <code>t3</code> 可以直接用清單裝載,在原函數 <code>check</code> 中可以接收到對應位置上的值清單。并且由于 <code>rise</code> 選項的開啟,位置和數量所構成的二進制組也會被提取出來,形成兩棵樹,即 <code>tr1</code> 、 <code>tr2</code> ,如下圖11所示
(圖11,[t1, t2, t3]作為清單參數,tr1, tr2作為傳回值樹)
此外,上升和下沉選項一個更加有效的使用例子是對 <code>torch.split</code> 和 <code>torch.stack</code> 函數進行裝飾,代碼如下所示
其中 <code>st</code> 即為合并後的樹,而 <code>splitted</code> 為再次拆分後的樹, <code>splitted</code> 和 <code>trees</code> 等價。
本文主要針對treevalue的核心特性——樹化函數,基于其自身進行了詳細的原了解析,受限于篇幅,本次隻着重講述了原生樹化函數本身的原理、特性以及例子。在下一篇中将會針對更多衍生場景進行分析與展示,敬請期待。
同時歡迎了解其他OpenDILab的開源項目:https://github.com/opendilab。