本文盡量避免數學公式,使用文字解釋列生成算法的原理,争取讓讀者能形成直覺上的了解。
列生成算法無法簡單地調用第三方庫來使用,必須根據具體問題,構造不同的算法模型。
隻有了解了原理,才能在踩到各種坑時,有所針對地去優化各種細節。不然隻能抓瞎或者抓腮。
列生成算法可以從兩個視角來了解:對偶角度和單純形算法角度。
這裡簡單過一下對偶的概念。
假設有個長得很标準的線性規劃問題:
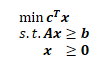
那麼,它的對偶問題為:
下面我們都以這個問題來讨論,即說到原問題時,預設是一個最小化問題;說到對偶問題時,預設是一個最大化問題。
怎麼了解這個對偶關系呢?借用經濟學方面的話來說,假設原問題的目标是讓成本最小,那麼對偶就是讓收入最大。更确切地講,是:
原問題丶:保證收入不低于某個值的條件下,使成本最小化。
對偶問題:保證成本不高于某個值的條件下,使收入最大化。
那個丶純粹是為了對齊,忽略之……
可以看到,原問題和對偶問題其實就是一個問題:目标淨收益最大。隻是一個是限制收入優化成本,一個是限制成本優化收入。角度不同而已。展現在公式上,就是原問題的變量對應對偶問題的限制,目标系數對應限制邊界,限制矩陣倒轉過來。
另外,關于對偶,一個比較重要的特性是:原問題的最優值與對偶問題的最優值相等。
列生成算法主要用途在于求解變量多,但是大部分變量将會取值為0的線性規劃問題。總體思路是先忽略大部分變量,構造一個隻使用小部分變量的模型(其餘變量相當于值為0),這樣就能很快求出一個解。然後尋找模型外的變量,找到能夠讓目标值更優的變量,加入模型再次求解。重複這個過程直至找不到更好的變量。
這個過程的關鍵問題在于,怎麼評估模型外的變量是否能讓目标值更優。
我們從對偶的角度來研究這個問題。
原問題的變量對應對偶問題的限制。是以原問題新增變量,相當于對偶問題新增限制。
原問題新增變量 -> 對偶問題新增限制
由于對偶問題是個最大化問題,是以對偶問題新增限制後,顯然最優值不變或變差,也就是不變或變小。從常理上看,限制越多,最優值越差嘛。
而前面提到的,原問題的最優值等于對偶問題的最優值。也就是說,如果對偶問題最優值不變,那麼原問題最優值也不變;如果對偶問題最優值變小,那麼原問題最優值也變小。而我們需要的正是讓原問題的最優值變小。
是以問題變為如何盡量避免新增的限制沒有改變最優值。設想一下,當加入新限制時,如果目前對偶的最優解沒有違反新的限制,那麼這個解仍然會是新增限制後的對偶問題的最優解,最優值将不變。
是以,我們要找的新增的限制,要和目前最優解沖突。
整條邏輯鍊為:
新增變量後原問題最優解變小 -> 新增限制後對偶問題最優解變小 -> 新增限制前的最優解不在新增限制後的可行域 -> 新增限制前的最優解不滿足新增的限制
一行對偶問題的限制的公式為:
假設最優解為w*,那麼違反限制的條件為:
變換一下,變成:
左側的式子,叫做的reduced cost,也叫做檢驗數。
通過分析,我們知道,隻要加入reduced cost小于0的對偶限制(進而加入了原問題對應的變量)即可。
很自然的想法是,我們更傾向于找到reduced cost最小的一個或幾個變量加入,也就是最好能找到最小化reduced cost的新限制:
這裡就出現了一個新的最優化問題。這個問題叫做列生成的子問題(sub problem)。其中w*是已知的,未知量是c和a。c和a是和問題的應用場景有關的,需要根據實際場景來構造c和a的限制條件。是以子問題無法通用地求解,隻能根據具體問題選擇不同的方法求解。
當所有未加入模型的變量的reduced cost都大于等于0時,目标值無法再優化,說明我們已得到最優解。
另外,熟悉對偶問題經濟學含義的同學會知道,reduced cost是指産品的差額成本。那麼顯然要新增的是差額成本為負的産品了。這是另一種了解列生成的思路。
對偶角度給出了一個偏感性的方式來了解列生成算法。換個視角,從單純形算法角度上看,則是單純形算法本身,為了更高效地求解包含大量變量的問題,自然地擴充為列生成算法。
相信有不少人被單純形算法虐得有心理陰影——公式複雜,手工計算量也巨大……
其實,如果我們先不看細節,單純形的核心原理并沒有那麼難以了解。下面講解時不會很嚴謹,了解算法架構就夠了。嚴謹的過程請參閱運籌學相關書籍。
衆所周知,單純形算法有一個幾何上的解釋:
線性規劃是一個凸優化問題,局部最優解就是全局最優解。
線性規劃的解空間是一個n維的凸多面體。最優解在這個凸多面體的某個頂點上。
單純形算法從一個初始頂點開始,不斷沿着鄰邊找更好的頂點。
當一個頂點四周沒有更好的頂點時,這個頂點就是最優解。
整個過程就像水沿着一條蜿蜒的溝渠流下,最終彙聚到最低點一樣。
問題是,這裡面的幾何概念和代數公式怎麼對應?
這裡用不嚴謹(但更容易了解)的語言說明一下:
邊界:解空間是由不等式限制(包括變量非負這些限制)圍起來的一塊空間區域。當點p使得若幹個不等式取等号時,那麼點p就在限制邊界的超平面上。這個邊界可能是一個面、邊、頂點。
頂點:頂點會讓盡量多的限制取等号。也就是說,頂點是由若幹個改為等号的限制組成的方程組的解。我們叫這個方程組為限制邊界方程組。
沿着邊:限制邊界方程組去掉一個方程,其解集就變成與頂點鄰接的一條邊。再取一條原方程組外的限制條件加入,所得到的解就是相鄰的頂點。簡單說,就是限制邊界方程組中替換掉一個方程,形成的新方程組解出來就是相鄰的頂點。
這裡涉及到通過讓限制取等号來求邊界的操作,而不等式亂糟糟地混在方程型的限制和變量非負限制裡,會使這裡的分析比較困難。是以使用單純形算法之前,都會通過引入松弛變量、剩餘變量和人工變量等方法(這一步在這裡不重要,不詳細展開了),将線性規劃轉換成如下标準形式:
标準形式中隻有變量非負限制包含不等式,其他限制都是等式。這樣我們就可以很容易地做邊界相關的計算了。假設變量數量為n,等式限制數量為m。通過轉換而來的标準形式都會有n > m。那麼,我們知道,隻要讓n-m個變量等于0,剩下的m個變量就可以通過這m個等式聯立方程組(限制邊界方程組)求出一個解(簡單起見,不考慮無解,無數解這些邊緣條件)。這個解就是一個頂點。
這裡限制邊界方程組中的m個變量叫作基變量,固定值為0的n-m個變量叫作非基變量。
沿着邊找相鄰頂點,就是取一個被固定為0的非負限制,也就是一個非基變量(這個操作叫入基),替換掉一個基變量(這個操作叫出基,這個變量出基後就固定值為0),然後重新求解一個頂點。
入基操作需要選擇入基變量,選擇的依據是這個變量在目标函數中的下降速度,也就是這個變量增加1時,目标值減少多少。經過推導可知,下降速度的計算公式剛好是檢驗數(reduced cost)。這裡就和對偶的視角聯系起來了。
出基操作這裡就不細說了,大緻的思路是在限制條件下,舊的基變量有一部分會随着入基變量的增長而下降,其中最先下降到0的舊的基變量就會被選為出基變量。
整個單純形算法的計算步驟是:
選取基變量和非基變量,簡單能出初始解就好。
計算所有非基變量的reduced cost,找到最小且為負值的那個作為入基變量。如果reduced cost都大于等于0,疊代終止。
選出基變量
解限制邊界方程組,回到步驟2
在單純形的步驟2,需要計算所有非基變量的RC。找到最小的那個。當變量個數很多的時候,這一步就成為了算法運作時間瓶頸。
在一些情況下,通過巧妙構造問題,可以讓這一步不需要周遊所有變量。甚至我們都不需要知道有多少變量,隻要能在每次疊代的時候生成一個或者多個變量,提升優化效果就可以了。
由于不需要周遊所有變量,是以一開始就不需要使用所有變量,隻需要使用一組能産生初始解的初始變量構成線性優化問題即可。這種隻使用部分變量的模型被稱為原問題的restricted master problem(RMP)。
每次疊代時,生成一個或多個讓reduced cost最小的變量加入RMP。這個生成步驟就是求解子問題。不斷加入新變量直到沒有小于0的reduced cost的變量時就達到最優解。
到這裡就和對偶角度分析的結果一緻了。
下面是單純形算法與列生成算法簡要流程圖的對比,可以看到,兩者的結構是一樣的。
一般來說,我們不會手搓單純形算法,是以正常都是直接調用單純形算法庫解RMP,然後做列生成,再跑RMP,直到達到最優。
這是一個列生成算法的經典例子。
原紙卷每個長17m,顧客們分别需要25個3m長,20個5m長,18個7m長的紙卷。
問:如何切割使消耗的原紙卷數量最少?
令一個原紙卷的切割方案集合為:
P = {(a, b, c) | 3a + 5b + 7c <= 17}
其中,a是一個原紙卷切割出的3m紙卷數量,b是5m紙卷數量,c是7m紙卷數量。
我們用變量x(abc)表示使用切割方案(a, b, c)的原紙卷數量。
顯然,一個變量與一個原紙卷切割方案一一對應。模組化如下:
這裡故意不适用傳統的下标序号标記,意在突出我們不需要對變量編号,隻需要知道變量在對應在什麼集合上,如何通過集合中的元素生成變量就行了。
初始解很好找。比如說我們可以取25個原紙卷按照方案(1, 0, 0)切割,20個原紙卷按照方案(0, 1, 0)切割,18個原紙卷按照方案(0, 0, 1)切割。這當然會有很多浪費。但是初始解可行就可以了,浪費的部分會在下面的疊代中優化掉。
接下來要生成變量。變量與切割方案一一對應的。是以是要找出一個切割方案(a, b, c),使得reduced cost最小。
其中w1、w2和w3分别為限制R1、R2和R3的對偶值。
限制條件除了a、b、c非負外,還需要滿足切割後的紙卷長度綜合小于或者等于原紙卷的長度。
這樣子問題就構造好了。求解子問題得到新增變量。然後疊代直到最優。具體計算這裡不展開了。
前面提到的單純形算法和列生成算法求解的都是線性規劃。在實際應用中,一般還會需要求解整數規劃。也就是變量都限制為整數的線性規劃。
這裡先提一個概念:整數規劃的線性松弛,整數規劃問題,不考慮整數限制,剩下的限制條件和目标組成的線性規劃問題。
其實我們并沒有很好的方法直接求解整數規劃,通常都是不斷地調整并求解線性松弛,最後找到最優整數解。
分支定界是一個用來求整數優化問題的架構。其實思路很簡單,就是采用類似二分法的技巧,線上性解空間中暴力搜尋整數解。
首先,求解線性松弛得到線性解。取一個變量x進行分支。比如x線性解值為1.2,那麼産生 x <= 1 和 x >= 2 兩個分支。将這兩個條件分别加入到線性松弛,得到兩個線性規劃。再求解這兩個線性規劃,兩個又分别分支……直到求得最優解。
有些情況下判斷一個解是否為最優解是有方法的,是以不用搜尋所有分支。但是,分支定界在最壞情況下的時間複雜度仍是指數級。為了防止運作時間過長,一般使用分支定界時還會額外加一些終止條件,比如回溯次數限制、運作時間限制、找到第一個整數解就結束等。
分支定價就是在分支定界架構中,使用列生成算法來求解每個分支節點的算法。
不過這裡,除了根節點,其他節點不用從頭開始生成新變量,繼承父節點用到的變量即可,這樣可以節省很多重複生成變量的過程。
在01整數規劃中,還有更簡化的方法,每次列生成得到線性松弛的最優解後,找出值最接近1的變量,新加這些變量等于1的限制,繼續跑列生成,直到找出是以值為1的變量。剩下的自然都是0了。這個方法可以加入回溯,也可以不回溯,出現無解就直接結束……據說不回溯也很少出現無解的情況。
通過RC找的新變量不一定能讓目标值變得更好,仍然存在不變的可能。極小機率的情況下,單純形算法可能會有入基變量和出基變量循環出現的情況。由于我們肯定是調用線性規劃庫來跑單純形的,是以不用考慮這個……
列生成沒有出基操作,不會出現循環。但是有一些改進會剔除備援變量,這時就會有極小機率會出現循環了。這種情況不需要費心去處理,玄學調參降低出現機率,并設定最大疊代次數等強制終止條件,確定能終止就好。
最惡心的情況是沒有循環,但是長時間沒有提升目标值的情況。這其實是算法卡在一個拐點上了,隻要過了拐點就能開始提升。特别是在一些限制較強的問題(比如密集的排班問題)中,使用某些啟發式算法或者手工做出來的初始解就很容易出現這種情況。
而我們為了避免算法跑太久,通常會設定多次疊代沒有提升就結束的條件。這可能使算法從拐點出發後,幾次疊代無優化就直接結束了。
這種情況無法完美解決。簡單的就是調參加更巧妙地設定結束條件,通過多次試驗盡量讓算法能跨過這個拐點。還有另一個技巧是可以适當地給限制邊界加一下噪音,比如說小于等于1的限制,可以放寬到小于等于1.0001。這樣從初始解出發疊代時,由于邊界寬松了一些,變量可以有些許變化,會讓目标值有一些微小的提升,幫助判斷是否需要結束疊代。
使用CPLEX時,我們可以很友善的設定變量的上下界。比如設定 0 <= x <= 1。這時,x <= 1這部分是會影響reduced cost的值的。而CPLEX接口計算的是沒有考慮這個條件的……是以可能你自己手搓代碼出來reduced cost和CPLEX接口出來的reduced cost不相等。
更嚴重的是,可能你會忘了 x <= 1 這個條件,導緻列生成的過程中算錯reduced cost。
這個問題其實影響不大,主要是會幹擾一些計算過程正确性的驗算。
沒有做分支操作時,線性松弛的目标值如果變差,說明子問題可能出現了一些很蠢的問題。
每次疊代求解線性規劃時,選用不同的算法會影響求解時間。根據經驗:
增加少量列時(列生成),使用單純形算法(Primal)。
增加少量限制時(分支),使用對偶單純形算法(Dual)。
其他情況,酌情使用對偶單純形算法或者内點法。通過試驗決定。
對偶單純形算法快的時候很快,慢的時候很慢。
内點法速度比較穩定。
以上也并不是所有場景通用的。應當針對具體問題,反複試驗來确定使用什麼算法。
Reduced cost可以用來評估變量的“有用”程度。越小表示變量越有用,越大表示變量越無關緊要。
列生成疊代次數較多後,變量數量會越來越多,進而每次疊代的運作速度越來越低。可以設定一個變量規模上限,當變量數量大于上限時,從模型中去掉reduced cost最大的那些變量。