論文動機
而在最近公布的 ICLR 2018 入圍名單中,另一篇資料增廣相關論文脫穎而出,而 SamplePairing 出局。仔細閱讀 Mixup 的論文,發現它其實是對 SamplePairing 的更進一步延伸。
名詞解釋
Empirical Risk Minimization (ERM):機器學習的經驗風險最小化,ERM 政策認為,經驗風險最小化的模型是最優化的模型。可參照李航的《統計學習方法》[1] 進行了解。
Βeta分布:既然機率論中的貝塔分布,是指一組定義在是指一組定義在(0,1)區間的連續機率分布,有兩個參數 α 和 β。論文中 α 和 β 相等。Βeta 分布的定義、機率密度函數和性質可參考 PRML [2]。
為了了解 Beta 分布,使用 Python 可視化 Beta 的模型。論文選擇的超參數是 α=0.2 和 0.4,此處主要觀察 α 變化對應的機率分布變化。
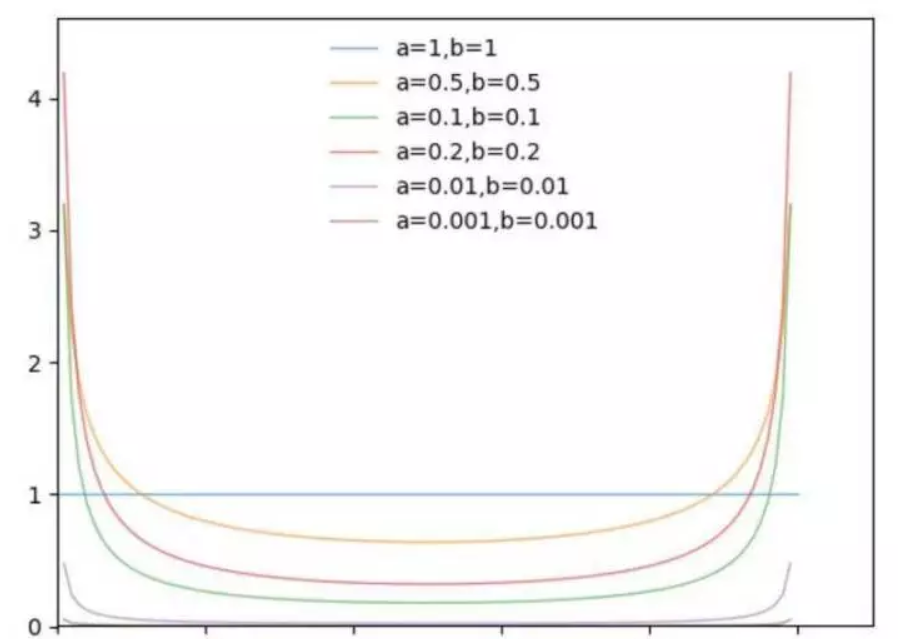
從上圖可以看出,α 趨近于 0 時,機率分布趨近于 x-0 和 x=1 兩種情況,在論文中代表 ERM。
模型細節
SamplePairing
SamplePairing 的實作很簡單,兩幅圖檔直接像素相加求平均,監督的 label 不變。但是在訓練過程中,先用 ILSVRC 資料集普通資料增廣方式,完成多個 epoch 後間歇性禁止 SamplePairing,在訓練損失函數和精度穩定後,禁止 SamplePairing 進行微調。
個人認為相當于随機引入噪聲,在訓練樣本中人為引入誤導性的訓練樣本。
mixup
△ mixup實作公式、Python源代碼和可視化實作
其中 (xi, yi) 和 (xj, yj) 是訓練集随機選取的兩個資料,λ ∈ [0,1],λ ∼ Beta(α,α)。
mixup 擴充訓練集分布基于這樣的先驗知識:線性特征向量的混合導緻相關目标線性混合。混合超參數 α 控制特征目标之間的插值強度,α→0 時表示 ERM。
mixup 模型實作方式簡單,PyTorch 7 行代碼即可實作。上圖中的可視化表明,mixup 導緻決策邊界模糊化,提供更平滑的預測。
實驗
論文的實驗過程很豐富,包括 CIFAR-10,CIFAR-100,和 ImageNet-2012,随機噪音測試,語音資料,facing adversarial examples 黑盒攻擊和白盒攻擊,UCI 資料集,以及穩定訓練 GAN 網絡。
對于具有代表性的 ImageNet-2012,Top-1 的精度至少提高 1.2%。
讨論
論文提出,在訓練過程中,随着 α 增加,訓練誤差越來越大,而在驗證驗證集測試中泛化誤差反而減少。這與論文提出的假設相同:mixup 隐含控制模型的複雜度。但是論文沒有提出 bias-variance trade-off 的理論解釋。
論文提出一些進一步探索的可行性:
mixup 是否可以應用在其他監督學習問題,比如回歸和結構化預測。mixup 可能在回歸問題容易實作,結構化預測如圖像分割等問題,實驗效果不明顯。
mixup 是否可以用于半監督學習、無監督學習或強化學習。當然作者是假設,希望有後來者證明 mixup 是理論可行的。
mixup 來自 MIT 和 Facebook AI Research。ICLR 是雙盲評審,官網上的匿名評審意見普遍認為 mixup 缺乏理論基礎,但是實驗效果具有明顯優勢。筆者個人認為在 mixup 基礎上,還有很多坑可以填。
原文釋出時間為:2018-03-7
本文作者:陳泰紅