函數 funtool
格式 funtool %該指令将生成三個圖形視窗,Figure No.1用于顯示函數f的圖形,Figure No.2用于顯示函數g的圖形,Figure No.3為一可視化的、可操作與顯示一進制函數的電腦界面。在該界面上由許多按鈕,可以顯示兩個由使用者輸入的函數的計算結果:加、乘、微分等。funtool還有一函數存儲器,允許使用者将函數存入,以便後面調用。在開始時,funtool顯示兩個函數f(x) = x與g(x) = 1在區間[-2*pi, 2*pi]上的圖形。Funtool同時在下面顯示一控制台,允許使用者對函數f、g進行儲存、更正、重新輸入、聯合與轉換等操作。
輸入指令funtool後,生成的界面如下:
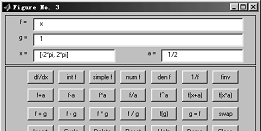
圖3-1 函數工具funtool界面
圖3-2 函數f的圖形 圖3-3 函數g的圖形
說明 文本輸入框區域:控制台的上面幾行,可以輸入文本;
f = :顯示代表函數f的符号表達式,可在該行輸入其他有效的表達式來定義f,再按Enter鍵即可在Figure No.1中畫出圖形;
g = :顯示代表函數g的符号表達式,可在該行輸入其他有效的表達式來定義g,再按Enter鍵即可在Figure No.2中畫出g圖形;
x = :顯示用于畫函數f與g的區間。可在該行輸入其他的不同區間,再按Enter鍵即可改變Figure No.1與Figure No.2中的區間;
a = :顯示一用于改變函數f的常量因子(見下面的操作按鈕)。可在該行輸入不同的常數。
控制按鈕區域:該區域有一些按鈕,按下它們将對函數f轉換成不同的形式與執行不同的操作。
df/dx:函數f的導數;
int f:函數f的積分(沒有常數的一個原函數),當函數f的原函數不能用初等函數表示時,操作可能失敗;
simple f:化簡函數f(若有可能);
num f:函數f 的分子;
den f:函數f的分母;
1/f:函數f的倒數;
finv:函數f的反函數,若函數f 的反函數不存在,操作可能失敗;
f+a:用f(x)+a代替函數f(x);
f-a:用f(x)-a代替函數f(x);
f*a:用f(x)+a代替函數f(x);
f/a:用f(x)/a代替函數f(x);
f^a:用f(x)^a代替函數f(x);
f(x+a):用f(x+a)代替函數f(x);
f(x*a):用f(x-a)代替函數f(x);
f+g:用f(x)+g(x)代替函數f(x);
f-g:用f(x)-g(x)代替函數f(x);
f*g:用f(x)*g(x)代替函數f(x);
f/g:用f(x)/g(x)代替函數f(x);
g=f:用函數f(x)代替函數g(x);
swap:函數f(x)與g(x)互換;
Insert:将函數f(x)儲存到函數記憶體清單中的最後;
Cycle:用記憶體函數清單中的第二項代替函數f(x);
Delete:從記憶體函數清單中删除函數f(x);
Reset:重新設定電腦為初始狀态;
Help:顯示線上的關于電腦的幫助;
Demo:運作該電腦的示範程式;
Close:關閉電腦的三個視窗。
指令1 極限
函數 limit
格式 limit(F,x,a) %計算符号表達式F=F(x)的極限值,當x→a時。
limit(F,a) %用指令findsym(F)确定F中的自變量,設為變量x,再計算F的極限值,當x→a時。
limit(F) %用指令findsym(F)确定F中的自變量,設為變量x,再計算F的極限值,當x→0時。
limit(F,x,a,'right')或limit(F,x,a,'left') %計算符号函數F的單側極限:左極限x→a- 或右極限x→a+。
例3-25
>>syms x a t h n;
>>L1 = limit((cos(x)-1)/x)
>>L2 = limit(1/x^2,x,0,'right')
>>L3 = limit(1/x,x,0,'left')
>>L4 = limit((log(x+h)-log(x))/h,h,0)
>>v = [(1+a/x)^x, exp(-x)];
>>L5 = limit(v,x,inf,'left')
>>L6 = limit((1+2/n)^(3*n),n,inf)
計算結果為:
L1 =
L2 =
inf
L3 =
-inf
L4 =
1/x
L5 =
[ exp(a), 0]
L6 =
exp(6)
指令2 導數(包括偏導數)
函數 diff
格式 diff(S,'v')、diff(S,sym('v')) %對表達式S中指定符号變量v計算S的1階導數。
diff(S) %對表達式S中的符号變量v計算S的1階導數,其中v=findsym(S)。
diff(S,n) %對表達式S中的符号變量v計算S的n階導數,其中v=findsym(S)。
diff(S,'v',n) %對表達式S中指定的符号變量v計算S的n階導數。
例3-26
>>syms x y t
>>D1 = diff(sin(x^2)*y^2,2) %計算
>>D2 = diff(D1,y) %計算
>>D3 = diff(t^6,6)
D1 =
-4*sin(x^2)*x^2*y^2+2*cos(x^2)*y^2
D2 =
-8*sin(x^2)*x^2*y+4*cos(x^2)*y
D3 =
720
指令3 符号函數的積分
函數 int
格式 R = int(S,v) %對符号表達式S中指定的符号變量v計算不定積分。注意的是,表達式R隻是函數S的一個原函數,後面沒有帶任意常數C。
R = int(S) %對符号表達式S中的符号變量v計算不定積分,其中v=findsym(S)。
R = int(S,v,a,b) %對表達式s中指定的符号變量v計算從a到b的定積分
R = int(S,a,b) %對符号表達式s中的符号變量v計算從a到b的定積分,其中v=findsym(S)。
例3-27
>>syms x z t alpha
>>INT1 = int(-2*x/(1+x^3)^2)
>>INT2 = int(x/(1+z^2),z)
>>INT3 = int(INT2,x)
>>INT4 = int(x*log(1+x),0,1)
>>INT5 = int(2*x, sin(t), 1)
>>INT6 = int([exp(t),exp(alpha*t)])
INT1 =
-2/9/(x+1)+2/9*log(x+1)-1/9*log(x^2-x+1)-2/9*3^(1/2)*atan(1/3*(2*x-1)*… 3^(1/2))-2/9*(2*x-1)/(x^2-x+1)
INT2 =
x*atan(z)
INT3 =
1/2*x^2*atan(z)
INT4 =
1/4
INT5 =
1-sin(t)^2
INT6 =
[ exp(t), 1/alpha*exp(alpha*t)]
指令4 常微分方程的符号解
函數 dsolve
格式 r = dsolve('eq1,eq2,…','cond1,cond2,…','v')
說明 對給定的常微分方程(組)eq1,eq2,…中指定的符号自變量v,與給定的邊界條件和初始條件cond1,cond2,….求符号解(即解析解)r;若沒有指定變量v,則預設變量為t;在微分方程(組)的表達式eq中,大寫字母D表示對自變量(設為x)的微分算子:D=d/dx,D2=d2/dx2,…。微分算子D後面的字母則表示為因變量,即待求解的未知函數。初始和邊界條件由字元串表示:y(a)=b,Dy(c)=d,D2y(e)=f,等等,分别表示,,;若邊界條件少于方程(組)的階數,則傳回的結果r中會出現任意常數C1,C2,…;dsolve指令最多可以接受12個輸入參量(包括方程組與定解條件個數,當然我們可以做到輸入的方程個數多于12個,隻要将多個方程置于一字元串内即可)。若沒有給定輸出參量,則在指令視窗顯示解清單。若該指令找不到解析解,則傳回一警告資訊,同時傳回一空的sym對象。這時,使用者可以用指令ode23或ode45求解方程組的數值解。
例3-28
>>D1 = dsolve('D2y – Dy =exp(x)')
>>D2 = dsolve('t*D2f = Df*log((Dy)/t)')
>>D3 = dsolve('(Dy)^2 + y^2 = 1','s')
>>D4 = dsolve('Dy = a*y', 'y(0) = b') % 帶一個定解條件
>>D5 = dsolve('D2y = -a^2*y', 'y(0) = 1', 'Dy(pi/a) = 0') % 帶兩個定解條件
>>[x,y] = dsolve('Dx = y', 'Dy = -x') % 求解線性微分方程組
>>[u,v] = dsolve(‘Du=u+v,Dv=u-v’)
-exp(x)*t+C1+C2*exp(t)
D2 =
y(t)=Int(exp(t*diff(f(t),`$`(t,2))/diff(f(t),t))*t,t)+C1
[ -1]
[ 1]
[ sin(s-C1)]
[ -sin(s-C1)]
D4 =
b*exp(a*t)
D5 =
cos(a*t)
x =
cos(t)*C1+sin(t)*C2
y =
-sin(t)*C1+cos(t)*C2
u =
1/2*C1*exp(2^(1/2)*t) - 1/4*C1*2^(1/2)*exp(-2^(1/2)*t) + 1/4*C1*2^(1/2) *exp (2^(1/2)*t) + 1/2*C1*exp(-2^(1/2)*t) - 1/4*C2*2^(1/2)*exp(-2^(1/2)*t) + 1/4*C2 *2^(1/2)*exp(2^(1/2)*t)
v =
-1/4*C1*2^(1/2)*exp(-2^(1/2)*t)+1/4*C1*2^(1/2)*exp(2^(1/2)*t)+1/2*C2*exp
(2^(1/2)*t)+1/4*C2*2^(1/2)*exp(-2^(1/2)*t)-1/4*C2*2^(1/2)*exp(2^(1/2)*t)+ 1/2*C2*exp(-2^(1/2)*t)
指令1 畫符号函數的等高線圖
函數 ezcontour
格式 ezcontour(f) %畫出二進制符号函數f=f(x,y)的等高線圖。函數f将被顯示于預設的平面區域[-2π<x<2π,-2π<y<2π]内。系統将根據函數變動的激烈程度自動選擇相應的計算栅格。若函數f在某些栅格點上沒有定義,則這些點将不顯示。
ezcontour(f,domain) %在指定的定義域domain内畫出二進制函數f(x,y),參量domain可以是四維向量[xmin,xmax,ymin,ymax]或二維向量[min,max](其中顯示區域為:min<x<max,min<y<max)。
ezcontour(…,n) %用指定n*n個栅格點(對定義域的一種劃分),在預設(若沒有指定)的區域内畫出函數f的圖形。n的預設值為60。
說明 該指令用函數表達式作為标題顯示,同時顯示坐标軸的恰當的刻度标簽。
例3-29
>>syms x y
>>f = (1-x)^2*exp(-(x^2)-(y+1)^2)-5*(x/5-x^3-y^5)*sin(-x^2-y^2)-1/3*exp(-(x+1)^2-y^2);
ezcontour(f,[-3,3],49)
圖形結果為圖3-4。
指令2 用不同顔色填充的等高線圖
函數 ezcontourf
格式 ezcontourf(f) %畫出二進制符号函數f=f(x,y)的等高線圖,且在不同的等高線之間自動用不同的顔色進行填充。函數f将被顯示于預設的平面區域[-2π<x<2π,-2π<y<2π]内。系統将根據函數變動激烈程度自動選擇相應的計算栅格。若函數f在某些栅格點上沒有定義,則這些點将不顯示。
ezcontourf(f,domain) %在指定的定義域domain内畫出二進制函數f(x,y)的等高線圖,且在不同的等高線之間自動用不同的顔色進行填充。定義域domain可以是四維向量[xmin,xmax,ymin,ymax]或二維向量[min,max](其中顯示區域為:min<x<max,min<y<max)。
ezcontourf(…,n) %用指定n*n個栅格點(對定義域的一種劃分),在預設(若沒有指定)的區域内畫出函數f的等高線圖,且在不同的等高線之間自動用不同的顔色進行填充。n的預設值為60。
例3-30
ezcontourf(f,[-3,3],64)
圖形結果為圖3-5。
圖3-4 等高線圖 圖3-5 等高線填充圖
指令3 符号函數的三維網格圖
函數 ezmesh
格式 ezmesh(f) %畫出二進制數學符号函數f=f(x,y)的網格圖。函數f将顯示于預設的平面區域[-2π<x<2π,-2π<y<2π]内。系統将根據函數變動的激烈程度自動選擇相應的計算栅格。若函數f在某些栅格點上沒有定義,則這些點将不顯示。
ezmesh(f,domain) %在指定的定義域domain内畫出二進制函數f(x,y)的網格圖,定義域domain可以是四維向量[xmin,xmax,ymin,ymax]或二維向量[min,max](其中顯示區域為:min<x<max,min<y<max)。
ezmesh(x,y,z) %在預設的矩形定義域範圍[-2π<s<2π,-2π<t<2π]内畫參數形式函數x=x(s,t)、y=y(s,t)、z=z(s,t)的二進制函數z=f(x,y)的網格圖。
ezmesh(x,y,z,[smin,smax,tmin,tmax]) %在指定的矩形定義域範圍[smin<s<smax,min<t<tmax]内畫參數形式函數x=x(s,t)、y=y(s,t)、z=z(s,t)的二進制函數z=f(x,y)的網格圖。
ezmesh(x,y,z,[min,max]) %用指定的矩形定義域[min<x<max,min<y<max]畫出函數z=f(x,y)的網格圖。
ezmesh(f,…,n) %用指定n*n個栅格點,在預設(若沒有指定)的區域内畫出函數f網的圖形。n的預設值為60。
ezmesh(…,'circ') %在一圓形區域(圓心位于定義域在中心)的範圍内畫出函數f的網格圖形。
例3-31
>>ezmesh(x*sin(-x^2-y^2),40,’circ’)
>>colormap [0 0 1]
圖形結果為:(圖3-6)
指令4 同時畫出曲面網格圖與等高線圖
函數 ezmeshc
格式 ezmeshc(f) %畫出二進制數學符号函數z=f(x,y)的網格圖形,同時在xy平面上顯示其等高線圖。函數f将被顯示于預設的平面區域[-2π<x<2π,-2π<y<2π]内。系統将根據函數變動的激烈程度自動選擇相應的計算栅格。若函數f在某些栅格點上沒有定義,則這些點将不顯示。
ezmeshc(f,domain) %在指定的定義域domain内畫出二進制函數f(x,y)的網格圖及其等高線圖,domain可以是四維向量[xmin,xmax,ymin,ymax]或二維向量[min,max](其中顯示區域為:min<x<max,min<y<max)。
ezmeshc(x,y,z) %在預設的矩形定義域範圍[-2π<s<2π,-2π<t<2π]内畫出參數形式函數x=x(s,t)、y=y(s,t)、z=z(s,t)的二進制函數z=f(x,y)的網格圖形與其等高線圖。
ezmeshc(x,y,z,[smin,smax,tmin,tmax]) %在指定的矩形定義域範圍[smin<s<smax,tmin<t<tmax]内畫出參數形式函數x=x(s,t)、y=y(s,t)、z=z(s,t)的二進制函數z=f(x,y)的網格圖形與其等高線圖。
ezsurfc(x,y,z,[min,max]) %用指定的定義域[min<x<max,min<y<max]畫出函數z=f(x,y)的網格圖與等高線圖。
ezmeshc(f,…,n) %用指定n*n個栅格點,在預設(若沒有指定)的區域内畫出函數f的網格圖形與等高線圖。n的預設值為60。
ezmeshc(…,'circ') %在一圓形區域(圓心位于定義域在中心)的範圍内畫出函數f的網格圖形及其等高線圖。
例3-32
>>ezmeshc(x*y/(1 + x^2 + y^2),[-5,5,-2*pi,2*pi],35)
圖形結果為圖3-7。
圖3-6 三維網格圖 圖3-7 網格等高線圖
指令5 畫符号函數的圖形
函數 ezplot
格式 ezplot(f) %對于顯式函數f=f(x),在預設的範圍[-π<x<π]上畫函數f(x);對于隐函數f=f(x,y),在預設的平面區域[-2π<x<2π,-2π<y<2π]上畫函數f(x,y)的圖形。
ezplot(f,[min,max]) %在指定的範圍[min<x<max]内畫函數表達式f=f(x)。若沒有圖形視窗存在,則該指令先生成标題為Figure No.1的新視窗,再在該視窗中操作;若已經有圖形視窗存在,則在标号最高的圖形視窗中進行操作。
ezplot(f,[xmin xmax],fign) %在指定标号fign的視窗中、指定的範圍[xmin xmax]内畫出函數f=f(x)的圖形。
ezplot(f,[xmin,xmax,ymin,ymax]) %在平面矩形區域[xmin<x<xmax, ymin<y <ymax]上畫出函數f(x,y)=0的圖形。
ezplot(x,y) %在預設的範圍0<t<2π内畫參數形式函數x=x(t)與y=y(t)的圖形。
ezplot(x,y,[tmin,tmax]) %在指定的範圍[tmin < t < tmax]内畫參數形式函數x=x(t)與y=y(t)的圖形。
ezplot(…,figure) %在由參量figure句柄指定的圖形視窗中畫函數圖形。
例3-33
>>ezplot(x^6-y^2)
圖形結果為圖3-8。
例3-34
>>syms x
>>ezplot(exp(x)*sin(x)/x)
>>grid on
圖形結果為圖3-9。
指令6 三維參量曲線圖
函數 ezplot3
格式 ezplot3(x,y,z) %在預設的範圍0<t<2π内畫空間參數形式的曲線x=x(t)、y=y(t)與z=z(t)的圖形。
ezplot3(x,y,z,[tmin,tmax]) %在指定的範圍tmin < t < tmax.内畫空間參數形式的曲線x=x(t)、y=y(t)與z=z(t)的圖形。
ezplot3(…,'animate') %以動畫形式畫出空間三維曲線。
圖3-8 隐函數圖 圖3-9 顯函數圖
例3-35
>>syms t;
>>ezplot3(t*sin(t), t*cos(t), t,[0,20*pi])
圖形結果為圖3-10。
指令7 畫極坐标圖形
函數 ezpolar
格式 ezpolar(f) %在預設的範圍0<theta<2π内畫極坐标函數rho=f(theta)的圖形。且将函數關系式顯示于圖形下方。
ezpolar(f,[a,b]) %在指定的範圍a<theta<b内畫極坐标函數rho=f(theta)的圖形。且将函數關系式顯示于圖形下方。
例3-36
>>syms t
>>ezpolar(1+cos(5*t))
圖形結果為圖3-11。
圖3-10 三維曲線圖 圖3-11 極坐标圖
指令8 三維帶顔色的曲面圖
函數 ezsurf
格式 ezsurf(f) %畫出二進制數學符号函數z=f(x,y)的曲面圖形。函數f将顯示于預設的平面區域[-2π<x<2π,-2π<y<2π]内。系統将根據函數的變動程度自動選擇相應的計算栅格。若函數f在栅格點上沒有定義,則這些點将不顯示。
ezsurf(f,domain) %在指定的定義域domain内畫出二進制函數f(x,y)的曲面圖形,domain可以是四維向量[xmin,xmax,ymin,ymax],或者是二維向量[min,max] (其中有min<x<max,min<y<max)。
ezsurf(x,y,z) %在預設的矩形定義域範圍-2π<s<2π,-2π<t<2π内畫出參數形式函數x=x(s,t)、y=y(s,t)與z=z(s,t)的曲面圖形。
ezsurf(x,y,z,[smin,smax,tmin,tmax])或ezsurf(x,y,z,[min,max]) %用指定的定義域畫出參數形式的曲面圖形
ezsurf(…,n) %用指定n*n個栅格點,在預設(若沒有指定)的區域内畫出函數f的圖形,n的預設值為60。
ezsurf(…,'circ') %在一圓形中心位于定義域在中心的範圍内畫出函數f的曲面圖形
例3-37
>>ezsurf(real(atan(x+i*y)))
圖形結果為圖3-12。
指令9 同時畫出曲面圖與等高線圖
函數 ezsurfc
格式 ezsurfc(f) %畫出二進制數學符号函數z=f(x,y)的曲面圖形與其等高線圖。函數f将顯示于預設的平面區域[-2π<x<2π,-2π<y<2π]内。系統将根據函數的變動程度自動選擇相應的計算栅格。若函數f在栅格點上沒有定義,則這些點将不顯示。
ezsurfc(f,domain) %在指定的定義域domain内畫出二進制函數f(x,y)的曲面圖形及其等高線圖,domain可以是四維向量[xmin,xmax,ymin,ymax]或二維向量[min,max](其中有min<x<max,min<y<max)。
ezsurfc(x,y,z) %在預設的矩形定義域範圍-2π<s<2π,-2π<t<2π内畫出參數形式函數x=x(s,t)、y=y(s,t)與z=z(s,t)的曲面圖形與等高線圖。
ezsurfc(x,y,z,[smin,smax,tmin,tmax])或ezsurfc(x,y,z,[min,max]) %用指定的定義域畫出參數形式的曲面圖形與等高線圖
ezsurfc(…,n) %用指定n*n個栅格點,在預設(若沒有指定)的區域内畫出函數f的曲面圖形與等高線圖,n的預設值為60。
ezsurfc(…,'circ') 在一圓形中心位于定義域的中心範圍内畫出函數f的曲面圖形與等高線圖
例3-38
>>ezsurfc(x*y/(1 + x^2 + y^2),[-5,5,-2*pi,2*pi],35,’circ’)
圖形結果為圖3-13。
圖3-12 三維曲面圖 圖3-13 三維曲面等高線圖
指令1 Fourier積分變換
函數 fourier
格式 F = fourier(f)
說明 對符号單值函數f中的預設變量x(由指令findsym确定)計算Fourier變換形式。預設的輸出結果F是變量w的函數:
若f = f(w),則fourier(f)傳回變量為t的函數:F= F(t)。
F = fourier(f,v) 對符号單值函數f中的指定變量v計算Fourier變換形式:
F = fourier(f,u,v) 令符号函數f為變量u的函數,而F為變量v的函數:
例3-39
>>syms x w u v
>>f = sin(x)*exp(-x^2); F1 = fourier(f)
>>g = log(abs(w)); F2 = fourier(g)
>>h = x*exp(-abs(x)); F3 = fourier(h,u)
>>syms x real
>>k = cosh(-x^2*abs(v))*sinh(u)/v
>>F4 = fourier(k,v,u)
F1 =
-1/2*i*pi^(1/2)*exp(-1/4*(w-1)^2)+1/2*i*pi^(1/2)*exp(-1/4*(w+1)^2)
F2 =
fourier(log(abs(w)),w,t)
F3 =
-4*i/(1+u^2)^2*u
F4 =
sinh(u)*(1/2*fourier(1/v*exp(x^2*abs(v)),v,u)-i*atan(u/x^2))
指令2 逆Fourier積分變換
函數 ifourier
格式 f = ifourier(F)
說明 輸出參量f = f(x)為預設變量w的标量符号對象F的逆Fourier積分變換。即:F = F(w) → f = f(x)。若F = F(x),ifourier(F)傳回變量t的函數:即:F = F(x) → f = f(t)。逆Fourier積分變換定義為:
f = ifourier(F,u) 使函數f為變量u(u為标量符号對象)的函數:
f = ifourier(F,v,u) 使F為變量v的函數,f為變量u的函數:
例3-40
>>syms w v x t
>>syms a real
>>f = sqrt(exp(-w^2/(4*a^2)));
>>IF1 = ifourier(f)
>>g = exp(-abs(x));
>>IF2 = ifourier(g)
>>h = sinh(-abs(w)) – 1;
>>IF3 = simple(ifourier(h,t))
>>syms w real
>>k = exp(-w^2*abs(v))*sin(v)/v;
>>IF4 = ifourier(k,v,t)
IF1 =
ifourier(exp(-1/4*w^2/a^2)^(1/2),w,x)
IF2 =
1/(1+t^2)/pi
IF3 =
-1/2*(pi*ifourier(exp(abs(w)),w,t)+pi*ifourier(exp(abs(w)),w,t)*t^2-… 1+2*pi*Dirac(t))/(1+t^2)/pi
IF4 =
1/2*(atan((t+1)/w^2)-atan((t-1)/w^2))/pi
指令3 Laplace變換
函數 laplace
格式 L = laplace(F)
說明 輸出參量L = L(s)為有預設符号自變量t的标量符号對象F的Laplace變換。即:F = F(t) → L = L(s)。若F = F(s),則fourier(F)傳回變量為t的函數L。
即:F = F(s) → L = L(t)。Laplace變換定義為:
laplace(F,t) 使函數L為變量t(t為标量符号自變量)的函數:
fourier(F,w,z) 使L為變量z的函數,F為變量w的函數:
例3-41
>>syms x s t v
>>f1= sqrt(t);
>>L1 = laplace(f)
>>f2 = 1/sqrt(s);
>>L2 = laplace(f2)
>>f3 = exp(-a*t);
>>L3 = laplace(f3,x)
>>f4 = 1 - sin(t*v);
>>L4 = laplace(f4,v,x)
1/(s-1/s^2)
(pi/t)^(1/2)
1/(x+a)
1/x-t/(x^2+t^2)
指令4 逆Laplace變換
函數 ilaplace
格式 F = ilaplace(L)
說明 輸出參量F = F(t)為預設變量s的标量符号對象L的逆Laplace變換
即:F = F(w) → f = f(x)。若L = L(t),則ifourier(L)傳回變量為x的函數F。即:F = F(x) → f = f(t)。逆Laplace變換定義為:
其中c為使函數L(s)的所有的奇點位于直線s = c左邊的實數。
F = ilaplace(L,y) 使函數F為變量y(y為标量符号對象)的函數:
F = ilaplace(L,y,x) 使F為變量x的函數,L為變量y的函數:
例3-42
>>syms a s t u v x
>>f = exp(x/s^2);
>>IL1 = ilaplace(f)
>>g = 1/(t-a)^2;
>>IL2 = ilaplace(g)
>>k = 1/(u^2-a^2);
>>IL3 = ilaplace(k,x)
>>y = s^3*v/(s^2+v^2);
>>IL4 = ilaplace(y,v,x)
IL1 =
ilaplace(exp(x/s^2),s,t)
IL2 =
x*exp(a*x)
IL3 =
1/(-a^2)^(1/2)*sin((-a^2)^(1/2)*x)
IL4 =
s^3*cos((s^2)^(1/2)*x)
指令5 Riemann ζ-函數
函數 zeta
格式 Y = zeta(X) %計算數值矩陣、或符号矩陣參量x中每一進制素的ζ-函數值。ζ-函數定義為:
Y = zeta(n, X) %傳回ζ(X)函數的n階導數
例3-43
>>Y1 = zeta(1.5)
>>Y2 = zeta(1.2:0.1:2.1)
>>Y3 = zeta([x 2;4 x+y])
>>DZ = diff(zeta(x),x,3)
Y1 =
2.6124
Y2 =
Columns 1 through 7
5.5916 3.9319 3.1055 2.6124 2.2858 2.0543 1.8822
Columns 8 through 10
1.7497 1.6449 1.5602
Y3 =
[ zeta(x,2), zeta(2,2)]
[ zeta(4,2), zeta(x+y,2)]
DZ =
zeta(3,x)
指令6 z-變換
函數 ztrans
格式 F = ztrans(f) %對預設自變量為n(就像由指令findsym确定的一樣)的單值函數f計算z-變換。輸出參量F為變量z的函數:f = f(n) → F = F(z)。函數f的z-變換定義為:
若函數f = f (z),則ztrans(f)傳回一變量為w的函數:f = f(z) → F = F(w)
F = ztrans(f,w) %用符号變量w代替預設的z作為函數F的自變量
F = ztrans(f,k,w) %對函數f中指定的符号變量k計算z-變換:
例3-44
>>syms a k w x n z
>>f1 = n^4;
>>ZF1 = ztrans(f)
>>f2 = a^z;
>>ZF2 = ztrans(g)
>>f3 = sin(a*n);
>>ZF3 = ztrans(f,w)
>>f4 = exp(k*n^2)*cos(k*n);
>>ZF4 = ztrans(f,k,x)
ZF1 =
z*(z^3+11*z^2+11*z+1)/(z-1)^5
ZF2 =
w/a/(w/a-1)
ZF3 =
-w*sin(a)/(-w^2+2*w*cos(a)-1)
ZF5 =
(x/exp(n^2)-cos(n))*x/exp(n^2)/(x^2/exp(n^2)^2-2*x/exp(n^2)*cos(n)+1)
指令7 逆z-變換
函數 iztrans
格式 f = iztrans(F)
說明 輸出參量f = f(n)為有預設變量z的單值符号函數F的逆z-變換。即:F = F(z) → f = f(n)。若F = F(n),則iztrans(F)傳回變量為k的函數f(k)。
即:F = F(n) → f = f(k)。逆z-變換定義為:,n =1,2,3,…
其中R為一正實數,它使函數F(z)在圓域之外 |z|≥R是解析的。
f = iztrans(F,k) 使函數f為變量k(k為标量符号對象)的函數f(k):,k=1,2,3,…
f = iztrans(F,w,k) 使函數F為變量w的函數,f為變量k的函數:,k=1,2,3,…
例3-45
>>syms a n k x z
>>f1= 2*z/(z^2+2)^2;
>>IZ1 = iztrans(f1)
>>f2 = n/(n+1);
>>IZ2 = iztrans(f2)
>>f3 = z/sqrt(z-a);
>>IZ3 = iztrans(f3,k)
>>f4 = exp(z)/(x^2-2*x*exp(z));
>>IZ4 = iztrans(f4,x,k)
IZ1 =
-1/8*sum(1/_alpha*(1/_alpha)^n,_alpha
IZ2 =
(-1)^k
IZ3 =
iztrans(z/(z-a)^(1/2),z,k)
IZ4 =
1/4*(-charfcn[0](k)-2*charfcn[1](k)*exp(z)+2^k*exp(z)^k)/exp(z)