CUDA實踐指南（十八）

矩陣乘法中的共享記憶體（$C = AA^T$）

先前矩陣乘法的一個變體可以用來說明如何處理對全局存儲器的分步通路以及共享存儲器組沖突。 這個變體隻是使用A的轉置來代替B，是以$C = AA^T$。

$C = AA^T$的簡單實作在Unoptimized處理對全局記憶體的跨步通路中顯示

未經優化的對全局存儲器的分步通路的處理：

在未優化的對全局存儲器的逐行通路的進行中，C的第row，th col元素是通過取A的第th行和第col行的點積獲得的。該核心的有效帶寬為3.64 GB / s在NVIDIA Tesla M2090上。 這些結果遠遠低于C = AB核心的相應測量結果。 不同之處在于，對于每個疊代i，在第二項中A的線程如何通路A中的元素[col TILE_DIM + i]。 對于線程變形，col表示A的轉置的順序列，是以col TILE_DIM表示跨度為w的跨步存取，導緻大量浪費的帶寬。

避免跨越通路的方式是像以前一樣使用共享記憶體，除非在這種情況下，warp會将一行A讀入共享記憶體塊的列中，如使用來自全局記憶體的合并讀取的優化處理跨步通路。

使用來自全局記憶體的合并讀取優化處理跨度通路：

使用來自全局記憶體的合并讀取對跨步通路進行優化處理時，使用共享transposeTile來避免點積中第二項中的未合并通路以及前一示例中共享的aTile技術，以避免第一項中的未合并通路。在NVIDIA Tesla M2090上，該核心的有效帶寬為27.5 GB / s。這些結果略低于最終核心對于C = AB所獲得的結果。造成差異的原因是共享記憶體組沖突。

for循環中transposedTile中元素的讀取沒有沖突，因為每個半變形的線程都會讀取瓦片的行，進而導緻跨單元的單元跨度。但是，從全局記憶體複制磁貼到共享記憶體時發生銀行沖突。為了使來自全局存儲器的加載能夠合并，資料從全局存儲器中順序讀取。然而，這需要以列的形式寫入共享記憶體，并且由于在共享記憶體中使用了wxw磁貼（tile），這導緻了w個銀行的線程之間的跨度 - 每個線程都經曆了同一個銀行。 （回想一下，對于計算能力為2.0或更高的裝置，w選為32）。這些多路銀行沖突非常昂貴。簡單的補救措施是填充共享記憶體數組，使其具有額外的列，如下面的代碼行所示。

這種填充消除了沖突，因為現線上程之間的跨度是w + 1個存儲體（即對于目前裝置是33個），由于用于計算存儲體索引的模算術，這相當于機關步長。 此次更改之後，NVIDIA Tesla M2090上的有效帶寬為39.2 GB / s，與上一次C = AB核心的結果相當。

表3總結了這些優化的結果。

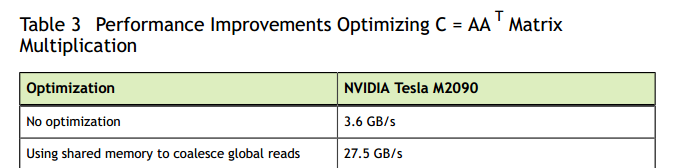
應該将這些結果與表2中的結果進行比較。從這些表中可以看出，合理使用共享記憶體可以顯着提高性能。

本節中的示例說明了使用共享記憶體的三個原因：

為了能夠對全局記憶體進行合并通路，特别是為了避免大步幅（對于一般矩陣，步幅遠遠大于32）

消除（或減少）來自全局記憶體的備援負載

避免浪費帶寬