1 案例背景
圖像融合,指通過對同一目标或同一場景用不同的傳感器(或用同一傳感器采用不同的方式)進行圖像采集得到多幅圖像,對這些圖像進行合成得到單幅合成圖像,而該合成圖像是單傳感器無法采集得到的。圖像融合所輸出的合成圖像往往能夠保持多幅原始圖像中的關鍵資訊,進而為對目标或場景進行更精确、更全面的分析和判斷提供條件。圖像融合屬于資料融合範疇,是資料融合的子集,兼具資料融合和圖像可視化的優點。是以,圖像融合能夠在一定程度上提高傳感器系統的有效性和資訊的使用效率,進而提高待分析目标的分辨率,抑制不同傳感器所産生的噪聲,改善圖像處理的效果。
圖像融合最早是以資料融合理論為基礎的,通過計算像素算術平均的方式得到合成圖像。該方法忽略了像素間的互相關系,往往會産生融合圖像的對比度差、可視化效果不理想等問題。是以,為了提高目标檢測的分辨率,抑制不同傳感器的檢測噪聲,本案例選擇了一種基于小波變換的圖像資料融合方法,首先通過小波變換将圖像分解到高頻、低頻,然後分别進行融合處理,最後再逆變換到圖像矩陣"。在融合過程中,為了盡可能保持多源圖像的特征,在小波分解的高頻域内,選擇圖像鄰域平均絕對值較大的系數作為融合小波重要系數;在小波分解的低頻域内,選擇對多源圖像的低頻系數進行權重平均作為融合小波近似系數。在反變換過程中,利用重要小波系數和近似小波系數作為輸入進行小波反變換。在融合圖像輸出後,對其做進一步的處理。實驗結果表明,基于小波變換的圖像資料融合方法運作效率高,具有良好的融合效果,并可用于廣泛的研究領域,具有一定的使用價值。
根據融合的作用對象,圖像融合一般可以分為3個層次:像素級圖像融合、特征級圖像融合和決策級圖像融合。其中,像素級融合是作用于圖像像素點最底層的融合,本章所研究的圖像融合是像素級圖像融合。
1.2理論基礎
傳統的直接像素算術平均進行圖像融合的方法往往會造成融合結果對比度降低、可視化效果不理想等問題,為此研究人員提出了基于金字塔的圖像融合方法,其中包括拉普拉斯金字塔、梯度金字塔等多分辨率融合方法。20世紀80年代中期發展起來的小波變換技術為圖像融合提供了新的工具,小波分解的緊緻性、對稱性和正交性使其相對于金字塔分解具有更好的圖像融合性能。此外,小波變換具有“數學顯微鏡”聚焦的功能,能實作時間域和頻率域的步調統一,能對頻率域進行正交分解,是以小波變換在圖像進行中具有非常廣泛的應用,已經被運用到圖像處理的幾乎所有分支,如圖像融合、邊緣檢測、圖像壓縮、圖像分割等領域。
假設對一維連續小波w…(t)和連續小波變換W,(a,b)進行離散化,其中,a表示尺度參數, b表示平移參數, 在離散化過程中分别取a=a{和b=bf, 其中, jeZ, a, >1,則對應的離散小波函數如下:
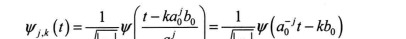
離散化的小波變換系數如下:
小波重構公式如下:
式中,C為常數且與資料信号無關。根據對連續函數進行離散化逼近的步驟,如果選擇的a, 和b, 越小, 則生成的網格節點就越密集, 所計算的離散小波函數wj x® 和離散小波系數Cj就越多,進而資料信号重構的精确度也越高。
由于數字圖像是二維矩陣,是以需要将一維信号的小波變換推廣到二維信号。假設(x)是一個一維的尺度函數,p(x)是相應的小波函數,那麼可以得到一個二維小波變換的基礎函數:
v’(x,y)=0(x)v(y)w(x,y)=y(x)(y)v(x,y)=V(x)w(y)
由于數字圖像是二維矩陣, 一般假設圖像矩陣的大小為NxN, 且N=2"(n為非負整數),是以經一層小波變換後,原始圖像便分解為4個分辨率為原來尺寸一的子帶區域,如圖11-1所示,分别包含了相應頻帶的小波系數,這一過程相當于在水準方向和垂直方向上進行隔點采樣。
進行下一層小波變換時,變換資料集中在LL子帶上。說明了圖像小波變換的數學原型。
(1)LL頻帶保持了原始圖像的内容資訊,圖像的能量集中于此頻帶:
對圖像進行小波變換的原理就是通過低通濾波器和高通濾波器對圖像進行卷積濾波,再進行二取一的下抽樣。是以,圖像通過一層小波變換可以被分解為1個低頻子帶和3個高頻子帶。其中,低頻子帶LL;通過對圖像水準方向和垂直方向均進行低通濾波得到;高頻子帶HL通過對圖像水準方向高通濾波和垂直方向低通濾波得到;高頻子帶LH通過對圖像水準方向低通濾波和垂直方向高通濾波得到:高頻子帶HH通過對圖像水準方向高通濾波和垂直方向高通濾波得到。各子帶的分辨率為原始圖像的,同理,對圖像進行二層小波變換時隻對低頻子帶LL進行, 可以将LLi子帶分解為LL 2、LH 2、HL 2和HH, 各子帶的分辨率為原始圖像的一。,以此類推可得到三層及更高層的小波變換結果。是以,進行
一層小波變換得到4個子帶,進行二層小波變換得到7個子帶,進行x層分解就得到3·x+1個子帶。如圖11-2所示為三層小波變換後的系數分布。
1 matlab版本
2014a
2 參考文獻
[1] 蔡利梅.MATLAB圖像處理——理論、算法與執行個體分析[M].清華大學出版社,2020.
[2]楊丹,趙海濱,龍哲.MATLAB圖像處理執行個體詳解[M].清華大學出版社,2013.
[3]周品.MATLAB圖像處理與圖形使用者界面設計[M].清華大學出版社,2013.
[4]劉成龍.精通MATLAB圖像處理[M].清華大學出版社,2015.