喜歡手寫學習,記憶深刻(字醜勿噴!)。
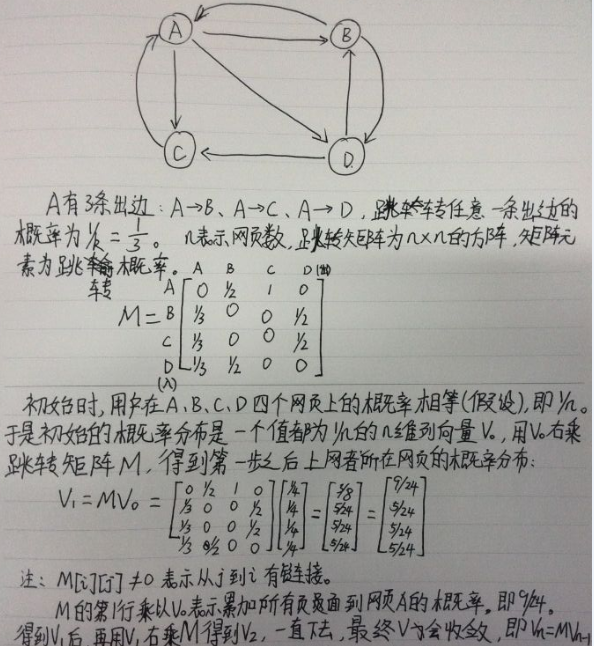
計算過程的代碼如下:
上面使用的圖是一個沒有太大缺陷的圖,其實PageRank中海油很多問題需要處理,主要問題有:
1.終止點問題
上述上網者的行為是一個馬爾科夫過程的執行個體,要滿足收斂性,需要具備一個條件:
圖是強連通的,即從任意網頁可以到達其他任意網頁:
網際網路上的網頁不滿足強連通的特性,因為有一些網頁不指向任何網頁,如果按照上面的計算,上網者到達這樣的網頁後便走投無路、四顧茫然,導緻前面累計得到的轉移機率被清零,這樣下去,最終的得到的機率分布向量所有元素幾乎都為0。假設我們把上面圖中C到A的連結丢掉,C變成了一個終止點,得到下面這個圖:
對應的轉移矩陣為:
連續疊代下去,最終所有元素都為0:
代碼如下:
2.陷阱問題
另外一個問題就是陷阱問題,即有些網頁不存在指向其他網頁的連結,但存在指向自己的連結。比如下面這個圖:
上網者跑到C網頁後,就像跳進了陷阱,陷入了漩渦,再也不能從C中出來,将最終導緻機率分布值全部轉移到C上來,這使得其他網頁的機率分布值為0,進而整個網頁排名就失去了意義。如果按照上面圖對應的轉移矩陣為:
不斷的疊代下去,就變成了這樣:
解決終止點問題和陷阱問題
上面過程,我們忽略了一個問題,那就是上網者是一個悠閑的上網者,而不是一個愚蠢的上網者,我們的上網者是聰明而悠閑,他悠閑,漫無目的,總是随機的選擇網頁,他聰明,在走到一個終結網頁或者一個陷阱網頁(比如兩個示例中的C),不會傻傻的幹着急,他會在浏覽器的位址随機輸入一個位址,當然這個位址可能又是原來的網頁,但這裡給了他一個逃離的機會,讓他離開這萬丈深淵。模拟聰明而又悠閑的上網者,對算法進行改進,每一步,上網者可能都不想看目前網頁了,不看目前網頁也就不會點選上面的連接配接,而上悄悄地在位址欄輸入另外一個位址,而在位址欄輸入而跳轉到各個網頁的機率是1/n。假設上網者每一步檢視目前網頁的機率為a,那麼他從浏覽器位址欄跳轉的機率為(1-a),于是原來的疊代公式轉化為:
現在我們來計算帶陷阱的網頁圖的機率分布:
重複疊代下去,得到:
可以看到C雖然占了很大一部分pagerank值,但其他網頁頁獲得的一些值,是以C的連結結構,它的權重确實應該會大些。