本文來自AI新媒體量子位(QbitAI)
深度學習大熱以後各種模型層出不窮,很多朋友都在問到底什麼是DNN、CNN和RNN,這麼多個網絡到底有什麼不同,作用各是什麼?
趁着回答《深度學習的主要分類是什麼呀?這些網絡cnn dbn dnm rnn是怎樣的關系?》這個問題的機會,我也想介紹一下主流的神經網絡模型。因為格式問題和傳播原因,我把原回答内容在這篇文章中再次向大家介紹。
在更詳細的介紹各種網絡前,首先說明:
大部分神經網絡都可以用深度(depth)和連接配接結構(connection)來定義,下面會具體情況具體分析。
籠統的說,神經網絡也可以分為有監督的神經網絡和無/半監督學習,但其實往往是你中有我我中有你,不必死摳字眼。
有鑒于篇幅,隻能粗略的科普一下這些非常相似的網絡以及應用場景,具體的細節無法展開詳談,有機會在專欄中深入解析。
文章中介紹的網絡包括:
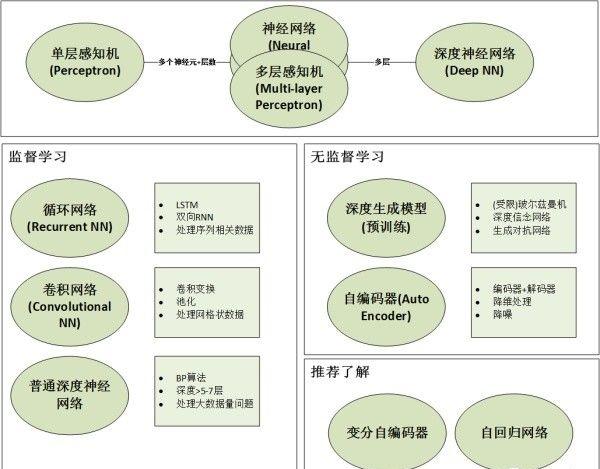
追根溯源的話,神經網絡的基礎模型是感覺機(Perceptron),是以神經網絡也可以叫做多層感覺機(Multi-layer Perceptron),簡稱MLP。單層感覺機叫做感覺機,多層感覺機(MLP)≈人工神經網絡(ANN)。
那麼多層到底是幾層?一般來說有1-2個隐藏層的神經網絡就可以叫做多層,準确的說是(淺層)神經網絡(Shallow Neural Networks)。随着隐藏層的增多,更深的神經網絡(一般來說超過5層)就都叫做深度學習(DNN)。
然而,“深度”隻是一個商業概念,很多時候工業界把3層隐藏層也叫做“深度學習”,是以不要在層數上太較真。在機器學習領域的約定俗成是,名字中有深度(Deep)的網絡僅代表其有超過5-7層的隐藏層。
神經網絡的結構指的是“神經元”之間如何連接配接,它可以是任意深度。以下圖的3種不同結構為例,我們可以看到連接配接結構是非常靈活多樣的。
需要特别指出的是,卷積網絡(CNN)和循環網絡(RNN)一般不加Deep在名字中的原因是:它們的結構一般都較深,是以不需要特别指明深度。想對比的,自編碼器(Auto Encoder)可以是很淺的網絡,也可以很深。是以你會看到人們用Deep Auto Encoder來特别指明其深度。
應用場景:全連接配接的前饋深度神經網絡(Fully Connected Feed Forward Neural Networks),也就是DNN适用于大部分分類(Classification)任務,比如數字識别等。但一般的現實場景中我們很少有那麼大的資料量來支援DNN,是以純粹的全連接配接網絡應用性并不是很強。
雖然很多時候我們把這兩種網絡都叫做RNN,但事實上這兩種網路的結構事實上是不同的。而我們常常把兩個網絡放在一起的原因是:它們都可以處理有序列的問題,比如時間序列等。
舉個最簡單的例子,我們預測股票走勢用RNN就比普通的DNN效果要好,原因是股票走勢和時間相關,今天的價格和昨天、上周、上個月都有關系。而RNN有“記憶”能力,可以“模拟”資料間的依賴關系(Dependency)。
為了加強這種“記憶能力”,人們開發各種各樣的變形體,如非常著名的Long Short-term Memory(LSTM),用于解決“長期及遠距離的依賴關系”。如下圖所示,左邊的小圖是最簡單版本的循環網絡,而右邊是人們為了增強記憶能力而開發的LSTM。
同理,另一個循環網絡的變種 - 雙向循環網絡(Bi-directional RNN)也是現階段自然語言處理和語音分析中的重要模型。開發雙向循環網絡的原因是語言/語音的構成取決于上下文,即“現在”依托于“過去”和“未來”。單向的循環網絡僅着重于從“過去”推出“現在”,而無法對“未來”的依賴性有效的模組化。
遞歸神經網絡和循環神經網絡不同,它的計算圖結構是樹狀結構而不是網狀結構。遞歸循環網絡的目标和循環網絡相似,也是希望解決資料之間的長期依賴問題。而且其比較好的特點是用樹狀可以降低序列的長度,從O(n)降低到O(log(n)),熟悉資料結構的朋友都不陌生。但和其他樹狀資料結構一樣,如何構造最佳的樹狀結構如平衡樹/平衡二叉樹并不容易。
應用場景:語音分析,文字分析,時間序列分析。主要的重點就是資料之間存在前後依賴關系,有序列關系。一般首選LSTM,如果預測對象同時取決于過去和未來,可以選擇雙向結構,如雙向LSTM。
卷積網絡早已大名鼎鼎,從某種意義上也是為深度學習打下良好口碑的功臣。不僅如此,卷積網絡也是一個很好的計算機科學借鑒神經科學的例子。卷積網絡的精髓其實就是在多個空間位置上共享參數,據說我們的視覺系統也有相類似的模式。
首先簡單說什麼是卷積。卷積運算是一種數學計算,和矩陣相乘不同,卷積運算可以實作稀疏相乘和參數共享,可以壓縮輸入端的次元。和普通DNN不同,CNN并不需要為每一個神經元所對應的每一個輸入資料提供單獨的權重。
與池化(pooling)相結合,CNN可以被了解為一種公共特征的提取過程,不僅是CNN大部分神經網絡都可以近似的認為大部分神經元都被用于特征提取。
以上圖為例,卷積、池化的過程将一張圖檔的次元進行了壓縮。從圖示上我們不難看出卷積網絡的精髓就是适合處理結構化資料,而該資料在跨區域上依然有關聯。
應用場景:雖然我們一般都把CNN和圖檔聯系在一起,但事實上CNN可以處理大部分格狀結構化資料(Grid-like Data)。舉個例子,圖檔的像素是二維的格狀資料,時間序列在等時間上抽取相當于一維的的格狀資料,而視訊資料可以了解為對應視訊幀寬度、高度、時間的三維資料。
說到生成模型,大家一般想到的無監督學習中的很多模組化方法,比如拟合一個高斯混合模型或者使用貝葉斯模型。深度學習中的生成模型主要還是集中于想使用無監督學習來幫助監督學習,畢竟監督學習所需的标簽代價往往很高…是以請大家不要較真我把這些方法放在了無監督學習中。
2.1.1. 玻爾茲曼機(Boltzmann Machines)和受限玻爾茲曼機(Restricted Boltzmann Machines)
每次一提到玻爾茲曼機和受限玻爾茲曼機我其實都很頭疼。簡單的說,玻爾茲曼機是一個很漂亮的基于能量的模型,一般用最大似然法進行學習,而且還符合Hebb’s Rule這個生物規律。但更多的是适合理論推演,有相當多的實際操作難度。
而受限玻爾茲曼機更加實際,它限定了其結構必須是二分圖(Biparitite Graph)且隐藏層和可觀測層之間不可以相連接配接。此處提及RBM的原因是因為它是深度信念網絡的構成要素之一。
應用場景:實際工作中一般不推薦單獨使用RBM…
2.1.2. 深度信念網絡(Deep Belief Neural Networks)
DBN是祖師爺Hinton在06年提出的,主要有兩個部分: 1. 堆疊的受限玻爾茲曼機(Stacked RBM) 2. 一層普通的前饋網絡。
DBN最主要的特色可以了解為兩階段學習,階段1用堆疊的RBM通過無監督學習進行預訓練(Pre-train),階段2用普通的前饋網絡進行微調。
就像我上文提到的,神經網絡的精髓就是進行特征提取。和後文将提到的自動編碼器相似,我們期待堆疊的RBF有資料重建能力,及輸入一些資料經過RBF我們還可以重建這些資料,這代表我們學到了這些資料的重要特征。
将RBF堆疊的原因就是将底層RBF學到的特征逐漸傳遞的上層的RBF上,逐漸抽取複雜的特征。比如下圖從左到右就可以是低層RBF學到的特征到高層RBF學到的複雜特征。在得到這些良好的特征後就可以用第二部分的傳統神經網絡進行學習。
多說一句,特征抽取并重建的過程不僅可以用堆疊的RBM,也可以用後文介紹的自編碼器。
應用場景:現在來說DBN更多是了解深度學習“哲學”和“思維模式”的一個手段,在實際應用中還是推薦CNN/RNN等,類似的深度玻爾茲曼機也有類似的特性但工業界使用較少。
2.1.3. 生成式對抗網絡(Generative Adversarial Networks)
生成式對抗網絡用無監督學習同時訓練兩個模型,核心哲學取自于博弈論…
簡單的說,GAN訓練兩個網絡:1. 生成網絡用于生成圖檔使其與訓練資料相似 2. 判别式網絡用于判斷生成網絡中得到的圖檔是否是真的是訓練資料還是僞裝的資料。生成網絡一般有逆卷積層(deconvolutional layer)而判别網絡一般就是上文介紹的CNN。自古紅藍出CP,下圖左邊是生成網絡,右邊是判别網絡,相愛相殺。
熟悉博弈論的朋友都知道零和遊戲(zero-sum game)會很難得到優化方程,或很難優化,GAN也不可避免這個問題。但有趣的是,GAN的實際表現比我們預期的要好,而且所需的參數也遠遠按照正常方法訓練神經網絡,可以更加有效率的學到資料的分布。
另一個常常被放在GAN一起讨論的模型叫做變分自編碼器(Variational Auto-encoder),有興趣的讀者可以自己搜尋。
應用場景:現階段的GAN還主要是在圖像領域比較流行,但很多人都認為它有很大的潛力大規模推廣到聲音、視訊領域。
自編碼器是一種從名字上完全看不出和神經網絡有什麼關系的無監督神經網絡,而且從名字上看也很難猜測其作用。讓我們看一幅圖了解它的工作原理…
如上圖所示,Autoencoder主要有2個部分:1. 編碼器(Encoder) 2. 解碼器(Decoder)。我們将輸入(圖檔2)從左端輸入後,經過了編碼器和解碼器,我們得到了輸出….一個2。但事實上我們真正學習到是中間的用紅色标注的部分,即數在低次元的壓縮表示。評估自編碼器的方法是重建誤差,即輸出的那個數字2和原始輸入的數字2之間的差别,當然越小越好。
和主成分分析(PCA)類似,自編碼器也可以用來進行資料壓縮(Data Compression),從原始資料中提取最重要的特征。認真的讀者應該已經發現輸入的那個數字2和輸出的數字2略有不同,這是因為資料壓縮中的損失,非常正常。
應用場景:主要用于降維(Dimension Reduction),這點和PCA比較類似。同時也有專門用于去除噪音還原原始資料的去噪編碼器(Denoising Auto-encoder)。
點選左下角“閱讀原文”,可解鎖更多作者的文章
還可以直接參與讨論~
量子位特約稿件,轉載請聯系原作者。
— 完 —
本文作者:阿薩姆
原文釋出時間:2017-10-03