神經網絡中的激活函數——加入一些非線性的激活函數，整個網絡中就引入了非線性部分，sigmoid 和 tanh作為激活函數的話，一定要注意一定要對 input 進行歸一話，但是 ReLU 并不需要輸入歸一化1 什麼是激活函數？ 2 神經網絡中為什麼要使用激活函數？ 1.sigmoid 2.tanh 3.ReLu 4.Leaky ReLu 5.PReLu 6.RReLu 7 Maxout 總結

激活函數，并不是去激活什麼，而是指如何把“激活的神經元的特征”通過函數把特征保留并映射出來（保留特征，去除一些資料中是的備援），這是神經網絡能解決非線性問題關鍵。

目前知道的激活函數有如下幾個：sigmoid,tanh，ReLu,softmax。 

simoid函數也稱S曲線：f(x)=11+e−x

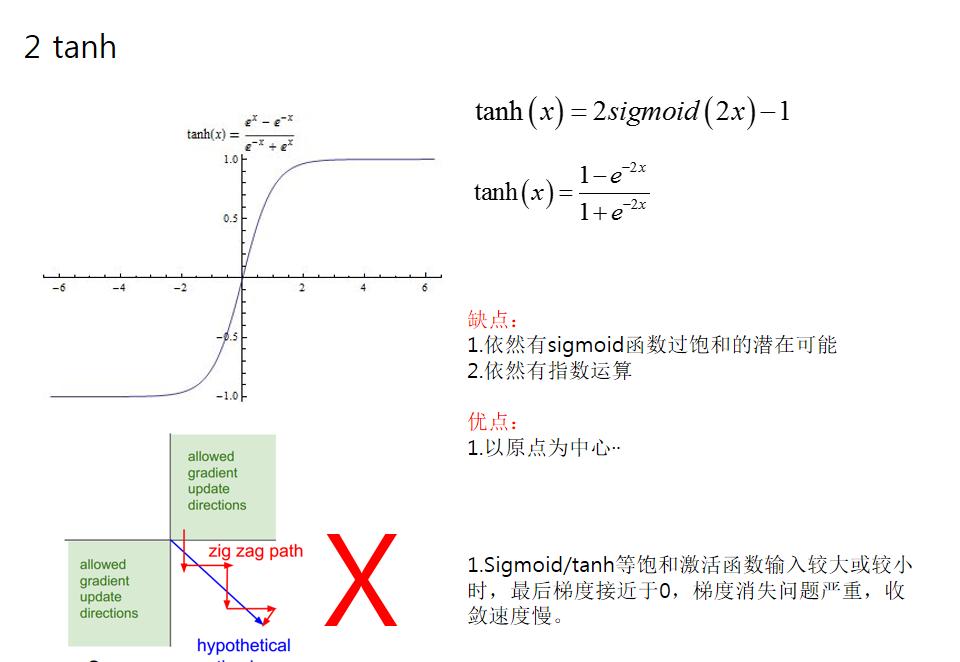
tanh:f(x)=tanh(x)

ReLU：f(x)=max(x,0)

softmax:f(x)=log(1+exp(x))

激活函數是用來加入非線性因素的，因為線性模型的表達力不夠

這句話字面的意思很容易了解，但是在具體處理圖像的時候是什麼情況呢？我們知道在神經網絡中，對于圖像，我們主要采用了卷積的方式來處理，也就是對每個像素點賦予一個權值，這個操作顯然就是線性的。但是對于我們樣本來說，不一定是線性可分的，為了解決這個問題，我們可以進行線性變化，或者我們引入非線性因素，解決線性模型所不能解決的問題。

這裡插一句，來比較一下上面的那些激活函數，因為神經網絡的數學基礎是處處可微的，是以選取的激活函數要能保證資料輸入與輸出也是可微的，運算特征是不斷進行循環計算，是以在每代循環過程中，每個神經元的值也是在不斷變化的。

這就導緻了tanh特征相差明顯時的效果會很好，在循環過程中會不斷擴大特征效果顯示出來，但有是，在特征相差比較複雜或是相差不是特别大時，需要更細微的分類判斷的時候，sigmoid效果就好了。

還有一個東西要注意，sigmoid 和 tanh作為激活函數的話，一定要注意一定要對 input 進行歸一話，否則激活後的值都會進入平坦區，使隐層的輸出全部趨同，但是 ReLU 并不需要輸入歸一化來防止它們達到飽和。

建構稀疏矩陣，也就是稀疏性，這個特性可以去除資料中的備援，最大可能保留資料的特征，也就是大多數為0的稀疏矩陣來表示。

其實這個特性主要是對于Relu，它就是取的max(0,x)，因為神經網絡是不斷反複計算，實際上變成了它在嘗試不斷試探如何用一個大多數為0的矩陣來嘗試表達資料特征，結果因為稀疏特性的存在，反而這種方法變得運算得又快效果又好了。

是以我們可以看到目前大部分的卷積神經網絡中，基本上都是采用了ReLU 函數。

摘自：http://blog.csdn.net/huahuazhu/article/details/74188288

神經網絡中如果不加入激活函數，其一定程度可以看成線性表達，最後的表達能力不好，如果加入一些非線性的激活函數，整個網絡中就引入了非線性部分，增加了網絡的表達能力。目前比較流行的激活函數主要分為以下7種：

參考文獻： 

[ReLu]:Rectifier Nonlinearities Improve Neural Network Acoustic Models 

[PRelu]:Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification

本文轉自張昺華-sky部落格園部落格，原文連結：http://www.cnblogs.com/bonelee/p/8242705.html，如需轉載請自行聯系原作者