排序算法（八）——基數排序

基數排序(Radix Sort)是在桶排序的基礎上發展而來的，兩種排序都是配置設定排序的進階實作。 配置設定排序(Distributive Sort)的基本思想：排序過程無須比較keyword，而是通過“配置設定”和“收集”過程來實作排序。它們的時間複雜度可達到線性階：O(n)。 先來看一下桶排序(Radix Sort)。

桶排序也稱為箱排序(Bin Sort)。其基本思想是：設定若幹個桶，依次掃描待排序的記錄R[0]，R[1]，…，R[n-1]，把keyword在某個範圍内的記錄全都裝入到第k個桶裡(配置設定)，然後按序号依次将各非空的桶首尾連接配接起來(收集)。 比如，要将一副混洗的52張撲克牌按點數A<2<…<J<Q<K排序，需設定13個“桶”。排序時依次将每張牌按點數放入相應的桶裡，然後依次将這些桶首尾相接，就得到了按點數遞增序排列的一副牌。 桶排序中。桶的個數取決于keyword的取值範圍。是以桶排序要求keyword的類型是有限類型。否則可能要無限個桶。 普通情況下每一個桶中存放多少個keyword同樣的記錄是無法預料的。故桶的類型應設計成連結清單為宜。 為保證排序是穩定的，配置設定過程中裝箱及收集過程中的連接配接必須按先進先出原則進行。 對于桶排序來說，配置設定過程的時間是O(n)；收集過程的時間為O(m)（採用連結清單來存儲輸入的待排序記錄）或O(m+n)。是以，桶排序的時間為O(m+n)。若桶個數m的數量級為O(n)，則桶排序的時間是線性的，即O(n)。 前面說的幾大排序算法 。大部分時間複雜度都是O(n2)，也有部分排序算法時間複雜度是O(nlogn)。而桶式排序卻能實作O(n)的時間複雜度。 但桶排序的缺點是：首先是空間複雜度比較高，須要的額外開銷大。排序有兩個數組的空間開銷，一個存放待排序數組。一個就是所謂的桶。比方待排序值是從0到m-1，那就須要m個桶。這個桶數組就要至少m個空間。 其次待排序的元素都要在一定的範圍内等等。 基數排序是對桶排序的一種改進，這種改進是讓“桶排序”适合于更大的元素值集合的情況。而不是提高性能。 我們還是用撲克牌的樣例來說明。 一張牌有兩個keyword組成：花色(桃<心<梅<方)+面值(A<2<3<4<...<K)。假如一張牌的大小首先被花色決定。同花色的牌有數字決定的話。我們就有兩種算法來解決問題。 即兩張牌，若花色不同，不論面值如何，花色低的那張牌小于花色高的。僅僅有在同花色情況下。大小關系才由面值的大小确定。這就是多關鍵碼排序。 為得到排序結果。我們讨論兩種排序方法。 方法1：先對花色排序。将其分為4個組，即梅花組、方塊組、紅心組、黑心組。再對每一個組分别按面值進行排序。最後。将4 個組連接配接起來就可以。 方法2：先按13 個面值給出13 個編号組(2 号。3 号，...，A 号)，将牌按面值依次放入相應的編号組，分成13 堆。再按花色給出4 個編号組(梅花、方塊、紅心、黑心)，将2号組中牌取出分别放入相應花色組，再将3 号組中牌取出分别放入相應花色組，……。這樣，4 個花色組中均按面值有序，然後。将4 個花色組依次連接配接起來就可以。 多關鍵碼排序依照從最主位關鍵碼到最次位關鍵碼或從最次位到最主位關鍵碼的順序逐次排序，分兩種方法： 最高位優先(Most Significant Digit first)法，簡稱MSD 法： 1）先按k1排序分組，将序列分成若幹子序列，同一組序列的記錄中。關鍵碼k1 相等。 2）再對各組按k2排序分成子組。之後，對後面的關鍵碼繼續這種排序分組。直到按最次位關鍵碼kd 對各子組排序後。 3）再将各組連接配接起來。便得到一個有序序列。 撲克牌按花色、面值排序中介紹的方法一即是MSD 法。 最低位優先(Least Significant Digit first)法。簡稱LSD 法： 1) 先從kd開始排序，再對kd-1進行排序，依次反複，直到按k1排序分組分成最小的子序列後。 2) 最後将各個子序列連接配接起來，便可得到一個有序的序列，撲克牌按花色、面值排序中介紹的方法二即是LSD 法。 對數字型或字元型的單keyword，能夠看作由多個數位或多個字元構成的多keyword。此時能夠採"配置設定-收集”的方法進行排序，這一過程稱作基數排序法，當中每一個數字或字元可能的取值個數稱為基數。比方，撲克牌的花色基數為4，面值基數為13。在整理撲克牌時，既能夠先按花色整理。也能夠先按面值整理。 按花色整理時，先按紅、黑、方、花的順序分成4摞（配置設定），再按此順序再疊放在一起（收集）。然後按面值的順序分成13摞（配置設定），再按此順序疊放在一起（收集），如此進行二次配置設定和收集就可以将撲克牌排列有序。 在“配置設定-收集”的過程中，須要保證排序的穩定性。 基數排序的思想就是将待排資料中的每組keyword依次進行桶配置設定。比方以下的待排序列：                 135、242、192、93、345、11、24、19 我們将每一個數值的個位，十位，百位分成三個keyword，比如： 135 -> k1(個位)=5  。k2(十位)=3 ，k3(百位)=1。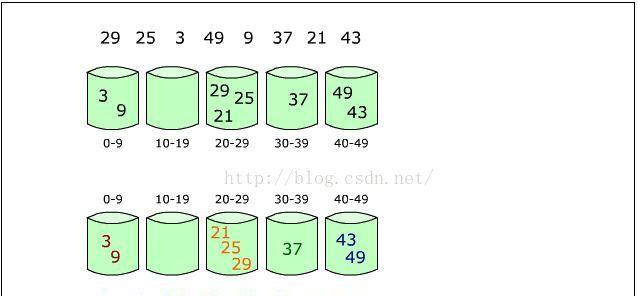

然後從最低位個位開始(從最次keyword開始)，對全部資料的k1keyword進行桶配置設定(由于，每一個數字都是 0-9的。是以桶大小為10)，再依次輸出桶中的資料得到以下的序列。 (11)、(242、192)、(93)、(24)、(135、345)、(19)（從最次keyword開始排序。忽略百位與十位，依照個位上的數字配置設定） 再對上面的序列接着進行針對k2的桶配置設定，輸出序列為： (11、19)、(24)、(135)、(242、345)、(192、93)（參考最次keyword來排序第二次keyword，忽略百位與個位，依照十位上的數字配置設定） 最後針對k3的桶配置設定，輸出序列為： (011、019、024、093)、(135、192)、(242)、(345)（參考第二次keyword來排序最高keyword。忽略十位與個位，依照百位上的數字配置設定） 排序完成。