uva 10245 - The Closest Pair Problem

<a target="_blank" href="http://uva.onlinejudge.org/index.php?option=com_onlinejudge&amp;Itemid=8&amp;category=24&amp;page=show_problem&amp;problem=1186">點選打開連結uva 10245</a>

題目意思：  

給定N個點，找到所有點中距離最小的

解題思路：

1：遞歸+分治

《網上大牛的解釋如下》

2在二維空間裡，可用分治法求解最近點對問題。預處理：分别根據點的x軸和y軸坐标進行排序，得到X和Y,很顯然此時X和Y中的點就是S中的點。

           1情況（1）：點數小于等于三時：                      

           2情況（2）：點數大于三時：

           3首先劃分集合S為SL和SR，使得SL中的每一個點位于SR中每一個點的左邊，并且SL和SR中點數相同。分别在SL和SR中解決最近點對問題，得到DL和DR，分别表示SL和SR中的最近點對的距離。令d=min(DL,DR)。如果S中的最近點對(P1,P2)。P1、P2兩點一個在SL和一個在SR中，那麼P1和P2一定在以L為中心的間隙内，以L-d和L+d為界

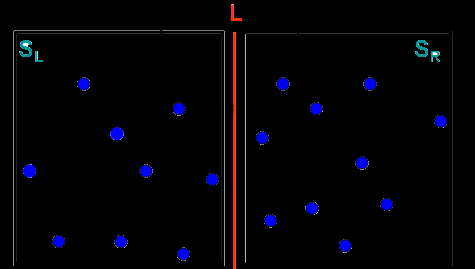
           4如果在SL中的點P和在SR中的點Q成為最近點對，那麼P和Q的距離必定小于d。是以對間隙中的每一個點，在合并步驟中，隻需要檢驗yp+d和yp-d内的點即可。

3《解題步驟》

步驟1：根據點的y值和x值對S中的點排序。

步驟2：找出中線L将S劃分為SL和SR

步驟3：将步驟2遞歸的應用解決SL和SR的最近點對問題，并令d=min(dL,dR)。

步驟4：将L-d~L+d内的點以y值排序，對于每一個點(x1,y1)找出y值在y1-d~y1+d内的所有點，計算距離為d'。如果d'小于d，令d=d'，最後的d值就是答案

代碼：