可以先看看這個視訊:
Perwork:
私鑰:Sender和Receiver預先約定加密和解密方案,向其他人保密。
這個實作比較難:向其他人保密。假如你是個商家,很多人要和你聯絡,發送者可能和你一點關系也沒有,怎麼保密。
需求:Sender素不相識,發送消息需求保密,加密方案必須公開。【就和信箱一樣,所有人都可以向你公開的的信箱裡投信件,但是隻有你才有鑰匙(私有的)取信件】
公鑰:加密方案向所有人公開,解密方案隻有Receiver知道,對其他所有人(包括Sender),Sender和除Receiver外所有人都是平等的,【Sender把信件放入Receive信箱了,Sender就不能再看到信件内容啦】
這就要求加密很容易,但是解密很難的算法!從跳闆裡跳入水裡容易,想跳回去就不是那麼容易啦。
先用一下示例講下流程:
1. 定義一個資訊集合
這個就是相當于26個英文字母,隻要知道這26個字母,你就可以拼出任何想要的資訊,隻是我們把26個擴充為了91個。
2. Sender 要發送的資訊為
這裡的Msg就是一個明文。
3. Sender 把資訊編碼為明文後,還要進行加密!
把明文的每一個元素都映射為另一個唯一的值(密文:可以公開的值)
簡單來說:加密過程為:
5
最後的保證:A和C絕對是一對一映射關系。
Question1: 那麼這個密文怎麼保證不被破解呢?
我們試下從這公開的加密公式和密文反推之
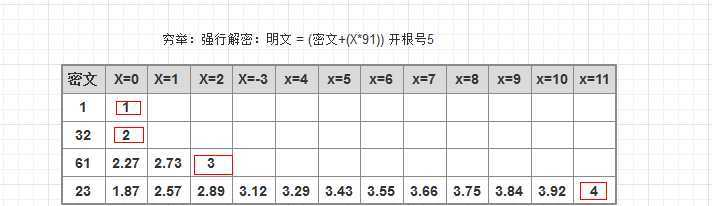
可以看出,通過窮舉,我們還是可以得到結果的,但這個計算次數也是指數增長的,且計算開根号得整數操作很要耗時,
一個算法最後逼得人隻能用窮舉來解密,那麼就是成功啦,
思考:如果公式裡面不是5次方,而是三位數,四位數的次方,那計算量就更大。
3 . sender把這密文發給Receiver 加密工作完成
4. 解密:Receive知道資訊比Sender多的就是這個91是怎麼來的,這個是關鍵。
4.1 91 = 7*13
(實作應用中,會設定為2個非常大的素數相乘,讓Sender看不出是哪2個素數來,我們為了示範簡單,假定Sender不會得到91=7*13這個結果,隻有Receiver知道)
這個算法就是利用了這一點:2個素數乘積的結果很容易,但是想反過來把結果反推為哪2個素數相乘很難。所有公開密鑰都是正着做容易,反過來就是很難
4.2 根據:和可以得到:
從以上可以“容易窮舉出一個”k=2時 :5*29 = 1+(13-1)*(7-1)*2
4.3 接着我們對密文C再乘29次方後對91取餘就可以直接得到明文啦
你隻要知道那個29,就可以得到破解啦!!!!!
是不是很神奇!!!!!!當然我們還是有很多迷惑的,比如:
為什麼選5,91,這些數字有什麼要求?接下來,我們先理一下上面的步驟:
步驟
示例
取2個大質數:p,q
p=7,q=13
密鑰:n=p*q,h 是一個與(p-1)(q-1)互質的數, 公開n 和 h
,p,q不公開
n =91,h = 5(與72互質)
加密(公開)C = Ah (mod n)
A = 明文,h=5,n=91,C= 密文
解密(保密)hd = 1+(p-1)(q-1)k---->A = C
d mod 91
5d = 1+72*k, 當k=2時,d=29成立
解密完成
密文乘方29 再對91取模 得到明文
原理證明 :
1. 取2個很大的不相等的質數p,q ;
2. m = p*q
3. 根據:比m小的質數個數r = φ(N) = φ(p)*φ(q) =
(p-1)*(q-1)
4. 選取一個與R互質的數e
5. 根據(輾轉相除)定理:2個互質的數一定滿足:e*x – r*y =1;
6. 上式等價為: e*d – r*k = 1;
7.密文c ,明文a , 加密 a e = c (mod m);
8. 解密: c d = a
(mod m),這個結論是 我們要證明的,
9. cd = ae*d = a 1+r*k =a*a
r*k
是以隻要證明: a*a r*k =
a(mod m) ---->a r*k = 1 (mod m)
10 .根據:
:
a r*k = (a k)r =
1 (mod m).
數學真有意思…….