通常,選擇交給學習算法處理特征的方式對算法的工作過程有很大影響。
例如:在前面的例子中,用\(x1\)表示房間大小。通過線性回歸,在橫軸為房間大小,縱軸為價格的圖中,畫出拟合曲線。回歸的曲線方程為:\(\theta_0+\theta_1x_1\),如下邊最左邊的圖。
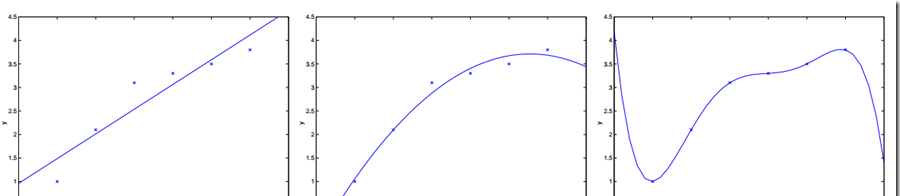
若定義特征集合為:\(x1\)表示房子大小,\(x2\)表示房子大小的平方,使用相同的算法,拟合得到一個二次函數,在圖中為一個抛物線,即:\(\theta_0+\theta_1x_1+\theta_2x_1^2\),如上邊中間的圖。
以此類推,若訓練集有7個資料,則可拟合出最高6次的多項式,可以找到一條完美的曲線,該曲線經過每個資料點。但是這樣的模型又過于複雜,拟合結果僅僅反映了所給的特定資料的特質,不具有通過房屋大小來估計房價的普遍性,而線性回歸的結果可能無法捕獲所有訓練集的資訊。
是以,對于一個監督學習模型來說,過小的特征集合使得模型過于簡單,過大的特征集合使得模型過于複雜。
對于特征集過小的情況,稱之為欠拟合(underfitting)
對于特征集過大的情況,稱之為過拟合(overfitting)
解決此類學習問題的方法:
1) 特征選擇算法:一類自動化算法,在這類回歸問題中選擇用到的特征
2) 非參數學習算法:緩解對于選取特征的需求,引出局部權重回歸
參數學習算法(parametric learning algorithm)
定義:參數學習算法是一類有固定數目參數,以用來進行資料拟合的算法。設該固定的參數集合為\(\theta\) 。線性回歸即是參數學習算法的一個例子
非參數學習算法(Non-parametric learning algorithm)
定義:一個參數數量會随m(訓練集大小)增長的算法。通常定義為參數數量随m線性增長。換句話說,就是算法所需要的東西會随着訓練集合線性增長,算法的維持是基于整個訓練集合的,即使是在學習以後。
算法思想:
假設對于一個确定的查詢點\(x\),在\(x\)處對你的假設\(h(x)\)求值。
對于線性回歸,步驟如下:
1) 拟合出\(\theta\),使 \(\sum_i(y^{(i)}-\theta^Tx^{(i)})^2\)最小
2) 傳回\(\theta^Tx\)
對于局部權重回歸,當要處理\(x\)時:
1) 檢查資料集合,并且隻考慮位于\(x\)周圍的固定區域内的資料點
2) 對這個區域内的點做線性回歸,拟合出一條直線
3) 根據這條拟合直線對\(x\)的輸出,作為算法傳回的結果
用數學語言描述即:
1) 拟合出\(\theta\),使 \(\sum_iw^{(i)}(y^{(i)}-\theta^Tx^{(i)})^2\)最小
2) \(w\)為權值,有很多可能的選擇,比如:
\[w^{(i)}=exp\bigg(-\frac{(x^{(i)}-x)^2}{2\tau^2}\bigg)\]
- 其意義在于,所選取的\(x^{(i)}\)越接近\(x\),相應的\(w^{(i)}\)越接近1;\(x^{(i)}\)越遠離\(x\),\(w^{(i)}\)越接近0。直覺的說,就是離得近的點權值大,離得遠的點權值小。
- 這個衰減函數比較具有普遍意義,雖然它的曲線是鐘形的,但不是高斯分布。\(\tau\)被稱作波長,它控制了權值随距離下降的速率。它越小,鐘形越窄,\(w\)衰減的很快;它越大,衰減的就越慢。
下圖就是\(x\)在(-1,1)之間,\(\tau\)為1的衰減函數圖:
x=-1:0.05:1;
y=exp(-x.*x/(2*1^2));
plot(x,y);
這樣對局部權重線性回歸,它的損失函數為:
\[J(\theta)=\sum\limits_{i=1}^{m}w^{(i)}\big[y^{(i)}-\theta^Tx^{(i)}\big]^2\]
算法思路:假設預測點取樣本點中的第i個樣本點(共m個樣本點),周遊1到m個樣本點(含第i個),算出每一個樣本點與預測點的距離,也就可以計算出每個樣本貢獻誤差的權值,可以看出w是一個有m個元素的向量(寫成對角陣形式),代入上式\(J(\theta)\)中。
\[w=\begin{bmatrix}
w_1& & & & \\
& \ddots& & & \\
& & w_i & & \\
& & & \ddots & \\
& & & & w_m
\end{bmatrix}\]
\[J(\theta)=\sum\limits_{i=1}^{m}w^{(i)}\big[y^{(i)}-\theta^Tx^{(i)}\big]^2=y^Twy-\theta^Tx^Twy-y^Tw^Tx\theta+\theta^Tx^Twx\theta\]
\[\bigtriangledown_{\theta}J(\theta)=0 \\ -x^Twy-x^Twy+2x^Twx\theta=0 \\ \theta=(x^Twx)^{-1}x^Twy\]
3) 傳回\(\theta^Tx\)
總結:對于局部權重回歸,每進行一次預測,都要重新拟合一條曲線。但如果沿着x軸對每個點都進行同樣的操作,你會得到對于這個資料集的局部權重回歸預測結果,追蹤到一條非線性曲線。
*局部權重回歸的問題:
由于每次進行預測都要根據訓練集拟合曲線,若訓練集太大,每次進行預測的用到的訓練集就會變得很大。
View Code
當波長\(\tau\)為1,這是回歸曲線接近一條直線,随着波長減小,回歸曲線更好的拟合樣本資料,但要注意過拟合的問題,選擇合适的波長值。
\(\tau=1\)
\(\tau=0.1\)
\(\tau=0.01\)