3.6 短時自相關分析
3.6.1 短時自相關函數
自相關函數用于衡量信号自身時間波形的相似性。由之前的博文介紹,清音和濁音的發生機理不同,因而在波形上也存在着較大的差異。濁音的時間波形呈現出一定的周期性,波形之間相似性較好;清音的時間波形呈現出随機噪聲的特性,雜亂無章,樣點間的相似性較差。這樣,可以用短時自相關函數來測定語音的相似特性。
時域離散确定信号的自相關函數定義為:
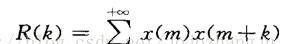
時域離散随機信号的自相關函數定義為:
若信号為一周期信号,周期為P,則:
上式說明,周期信号的自相關函數也是一個同樣周期的周期信号,自相關函數具有下述性質:
1.對稱性:
2.在k = 0處為最大值,即對于所有k來說,
3.對于确定信号,值R(0)對應于能量,而對于随機信号,R(0)對應于平均功率
上述的第2個性質中,如果是一個周期為P的信号,則在取樣
處,其自相關函數也是最大值,是以可以根據自相關函數的最大值的位置來估計周期信号的周期值。
3.6.2 語音信号的短時自相關函數
對于語音來說,采用短時分析方法,可以定義短時自相關函數為:
因為
,是以
定義
那麼最初的短時自相關函數可以寫成:
是以,短時自相關函數的框圖表示為:
下面來看一下濁音以及清音的短時自相關函數:
濁音的短時自相關函數:
清音的短時自相關函數:
濁音和清音的短時自相關函數有如下幾個特點:
1.短時自相關函數可以很明顯的反映出濁音信号的周期性。
2.清音的短時自相關函數沒有周期性,也不具有明顯突出的峰值,其性質類似于噪聲。
3.不同的窗對短時自相關函數結果有一定的影響。采用矩形窗時,濁音自相關曲線的周期性顯示出比用漢明窗更明顯的周期性。其主要原因是加漢明窗後,語音段兩端的幅度逐漸下降,進而模糊了信号的周期性。
窗長對濁音的短時自相關性有着直接的影響。一方面,由于語音信号的特性是變化的,是以要求N應盡量小。但與之沖突的另一方面是為了充分反映語音的周期性,又必須選擇足夠寬的窗,以使得選出的與語音段包含兩個以上的基音周期。
計算短時自相關函數需要很大的運算量,有時為簡化運算,常使用一種與自相關函數有相似作用的另一參量,即短時平均幅度差函數(AMDF)。
3.6.4 短時平均幅度差函數
對一個周期為P的周期信号x(n)來說,在k=
時,
=0(k=
)。對于濁音語音,在基音周期的整數倍上,d(n)總是很小,但不是零,是以,可以定義短時平均幅度差函數AMDF為:
顯然,如果x(n)具有周期P,則當
具有最小值。應該注意的是,取矩形窗是很合适的。